Алгебралық амалдар және олардың кейбір кластары. Топтар

Коммутативтік және ассоциативтік амалдар

Бейтарап (нейтрал) және кері элементтер. Кері амалдар

Топ ұғымы, мысалдар. Топтың қарапайым қасиеттері

Ішкі топтар

Математикалық амалдардың қасиеттерін зерттейтін саласы алгебра деп аталады.

Қандай да бір 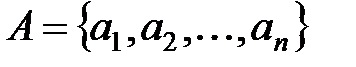жиыны элементтерінен құрылған реттелген теруді ұзындығы 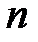-ге тең кортеж деп атайды. Белгіленуі:

.

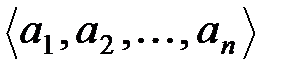Барлық осындай кортеждердің жиынын 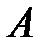жиынының 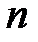-ші декарттық дәрежесі деп атайды. Белгіленуі: .

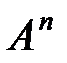Анықтама. 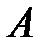жиынындағы алгебралық амал деп 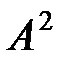-нің әрбір 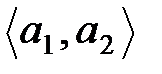кортежіне 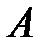жиынының анықталған 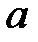элементін сәйкес қоятын бейнелеуді айтады; 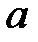элементін 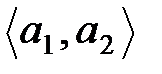кортежіне қолданған амалдың нәтижесі немесе 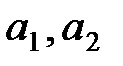элементтерінің композициясы деп атайды.

Мысалы, қосу, көбейту және азайту амалдарын 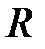нақты сандар жиынындағы амалдар ретінде қарастыруға болады. Сонымен қатар, үш өлшемді кеңістіктің векторлар жиынындағы векторлық көбейтінді амалы, 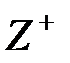бүтін оң сандар жиынындағы дәрежеге шығару амалы, 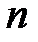-ші ретті барлық квадратты матрицалар жиынындағы квадратты матрицалардың көбейтіндісі алгебралық амалдар болып табылады.

Алгебралық амалдарды белгілеу үшін , таңбаларын немесе арнайы таңбаларды, мысалы қосу (+), азайту (-) және көбейту ( ) таңбаларын пайдалануға болады. 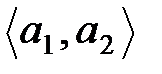кортежіне амалды қолдану нәтижесін сәйкесінше 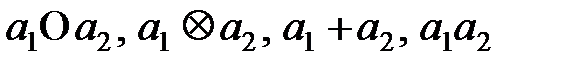түрлерінде жазамыз.

Біздің анықтаған амалымызды екіорынды немесе бинарлық амал деп атайды.

Анықтама. 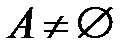жиынында бинарлық амал берілген деп аталады, егер осы жиынның реттелген екі элементіне сәйкес келетін үшінші элементті анықтайтын ереже берілген болса.

амалы; ,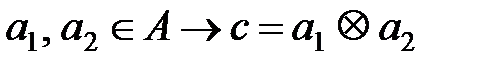

мұндағы, 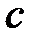элементі 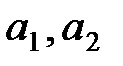элементтеріне амалын қолданғанда пайда болған элемент.

Мысал 2.1.1. 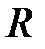- нақты сандар жиыны.

1) ;

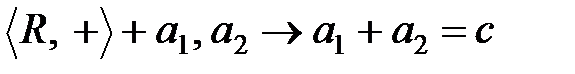2) ,

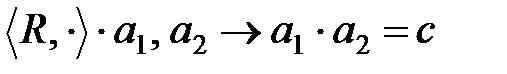3) 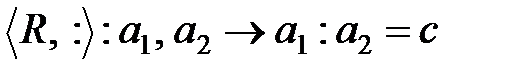, ал егер 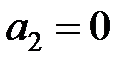болса, онда 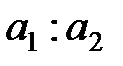анықталмайды, сол себепті: бинарлық амал емес.

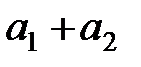амалындағы қосу таңбасын аддитивті заңдылық деп, ал 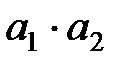амалындағы көбейту таңбасын мультипликативті заңдылық деп те атайды.

Анықтама. Бір элементке бір элементті сәйкес қоятын амал унарлы деп аталады, яғни:

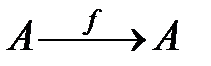
бейнелеуін айтады.

Осылайша үш орынды 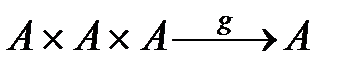үштік (тренарлық) және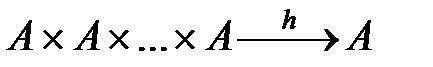 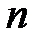-арлық амалдар да анықталады.

Анықтама. 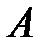жиынындағы 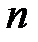-орынды амал деп 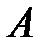жиынындағы әрбір 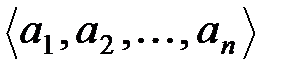кортежіне осы 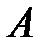жиынының анықталған бір 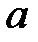элементін сәйкес қоятын бейнелеуді айтады.

Егер 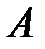жиынында - амал анықталған болса, онда оны 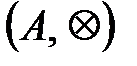деп белгілейміз және оны алгебралық жүйе деп атаймыз. 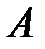жиыны алгебралық жүйенің негізгі жиыны болып есептеледі.

Мысалы: 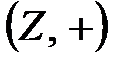, , 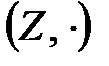, , 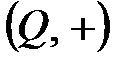, 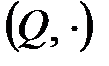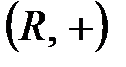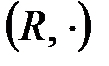- алгебралық жүйелер.