Топ ұғымы, мысалдар. Топтың қарапайым қасиеттері
Анықтама. Ассоциативтік және кері амалы анықталған бос емес 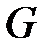 жиыны берілген амалға қатыстытоп деп аталады.
жиыны берілген амалға қатыстытоп деп аталады.
Басқаша айтқанда, ассоциативтік амалымен 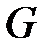 жиыны топ болып табылады, егер кез келген екі
жиыны топ болып табылады, егер кез келген екі 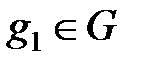 және
және 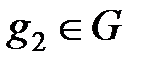 элементтері үшін әрбір
элементтері үшін әрбір
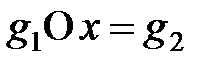 және
және 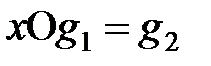
теңдеулерінің жалғыз бір ғана шешімдері бар болса.
Топ анықтамасындағы кері амалдың болуы шартын келесі шарттармен ауыстыруға болады:
10. Кез келген 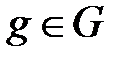 элементі үшін
элементі үшін
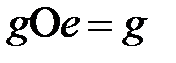 ,
, 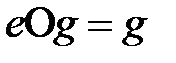
теңдіктері орындалатындай 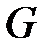 жиынында
жиынында 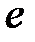 бейтарап элементі бар болады.
бейтарап элементі бар болады.
20. Әрбір 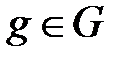 элементі үшін
элементі үшін
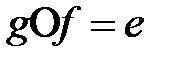 ,
, 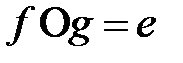
теңдіктерін қанағаттандыратын 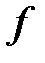 кері элементі бар болады.
кері элементі бар болады.
Әдетте кері амалдың болу шартының орнына 10, 20 шарттарды тексерген ыңғайлы.
Сонымен, 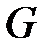 жиынында
жиынында  амалы анықталып, ол төмендегі үш шартты қанағаттандырса, онда
амалы анықталып, ол төмендегі үш шартты қанағаттандырса, онда 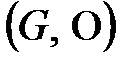 жүйені топ деп атайды:
жүйені топ деп атайды:
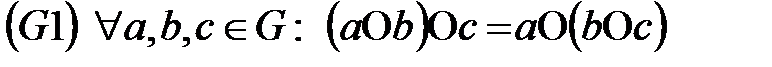 ,
,
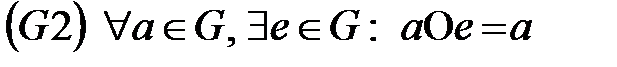 ,
,
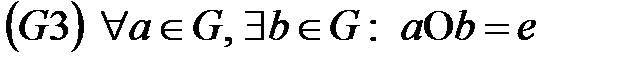 .
.
Бұл қасиеттерді топтың аксиомалары деп атайды.
Мысал 2.1.7
а) 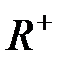 оң нақты сандар жиыны көбейту амалына қатысты топ құрайды, өйткені көбейту амалы ассоциативті, 1 саны – бейтарап элемент (кез келген
оң нақты сандар жиыны көбейту амалына қатысты топ құрайды, өйткені көбейту амалы ассоциативті, 1 саны – бейтарап элемент (кез келген 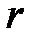 саны үшін
саны үшін 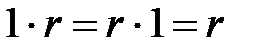 ) болып табылады және әрбір
) болып табылады және әрбір 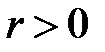 саны үшін
саны үшін 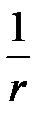 -ге тең
-ге тең 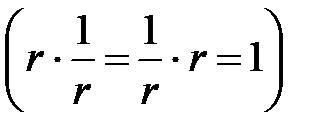 кері саны бар болады. Бұл топ оң нақты сандардың мультипликативтік тобы деп аталады. «multiplicatio» (латын сөзінен шыққан) мағынасы - «көбейту» дегенді білдіреді.
кері саны бар болады. Бұл топ оң нақты сандардың мультипликативтік тобы деп аталады. «multiplicatio» (латын сөзінен шыққан) мағынасы - «көбейту» дегенді білдіреді.
ә) Барлық  нақты сандар жиыны қосу амалына қатысты топ құрайды, өйткені қосу амалы ассоциативті, 0 саны - бейтарап элемент (кез келген
нақты сандар жиыны қосу амалына қатысты топ құрайды, өйткені қосу амалы ассоциативті, 0 саны - бейтарап элемент (кез келген  саны үшін
саны үшін 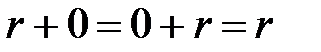 ) болып табылады және кез келген
) болып табылады және кез келген 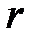 саны үшін қарама-қарсы
саны үшін қарама-қарсы 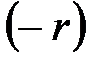 саны (яғни
саны (яғни 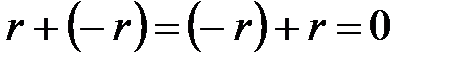 ) кері элемент болады. Бұл топ нақты сандардың аддитивтік тобы деп аталады. «additio» (латын сөзінен шыққан) мағынасы - «қосу» дегенді білдіреді.
) кері элемент болады. Бұл топ нақты сандардың аддитивтік тобы деп аталады. «additio» (латын сөзінен шыққан) мағынасы - «қосу» дегенді білдіреді.
б) Арифметикалық 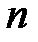 -өлшемді векторлық кеңістік векторларды қосу амалына қатысты топ құрайды, өйткені бұл амал ассоциативті,
-өлшемді векторлық кеңістік векторларды қосу амалына қатысты топ құрайды, өйткені бұл амал ассоциативті, 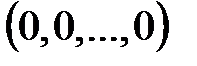 нөлдік векторы – бейтарап элемент,
нөлдік векторы – бейтарап элемент, 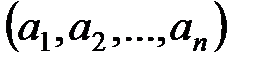 векторы үшін
векторы үшін 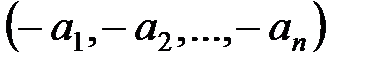 векторы кері элемент болып табылады.
векторы кері элемент болып табылады.
Мультипликативтік топта: бейтарап элементті топтың бірлігі деп атайды; 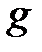 элементі үшін кері элементті
элементі үшін кері элементті 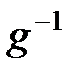 деп белгілейді; көбейту амалын және оны
деп белгілейді; көбейту амалын және оны 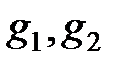 элементтеріне қолдану нәтижесін
элементтеріне қолдану нәтижесін 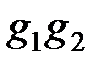 арқылы белгілейді. Бұл мультипликативтік терминология деп аталады.
арқылы белгілейді. Бұл мультипликативтік терминология деп аталады.
Аддитивтік топта: бейтарап элементті топтың нөлі деп атайды; 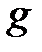 элементі үшін кері элементті
элементі үшін кері элементті 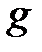 -ге қарама-қарсы
-ге қарама-қарсы 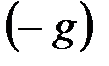 арқылы белгілейді; қосу амалын және оны
арқылы белгілейді; қосу амалын және оны 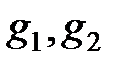 элементтерімен
элементтерімен 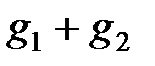 арқылы белгілейді. Бұл аддитивтік терминология деп аталады.
арқылы белгілейді. Бұл аддитивтік терминология деп аталады.
Коммутативтік амалы бар топты коммутативтік топ деп атайды.
Шектеулі 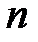 элементтер санынан тұратын топты
элементтер санынан тұратын топты 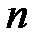 ретті шекті топ деп атайды, ал шектеусіз элементтер жиыны бар топты шексіз топ деп атайды.
ретті шекті топ деп атайды, ал шектеусіз элементтер жиыны бар топты шексіз топ деп атайды.
Практикада көп жағдайларда топтың негізгі амалы қосу (+) амалымен кезігеді. Бұл жағдайда 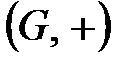 топты аддитивті топ деп атайды.
топты аддитивті топ деп атайды.
Ал көбейту (  ) немесе көбейтуге ұқсас амалмен берілген
) немесе көбейтуге ұқсас амалмен берілген 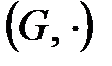 топтарды мультипликативті топтар деп атайды. Сан жиындарында аддитивті топтың бірлігі 0 (ноль) болады да, мультипликативті топтың бірлігі 1 (бір) болады. Бұл екі жазылудың айырмашылығы мына кестеде көрсетілген:
топтарды мультипликативті топтар деп атайды. Сан жиындарында аддитивті топтың бірлігі 0 (ноль) болады да, мультипликативті топтың бірлігі 1 (бір) болады. Бұл екі жазылудың айырмашылығы мына кестеде көрсетілген:
| Амал | Бейтарап элемент | Кері элемент | |
| Жалпы жағдай | 
| 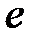 - бірлік - бірлік
| 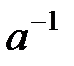 - кері - кері
|
| Мультипликативті |  көбейту көбейту
| 1 - бірлік | 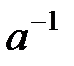 - кері - кері
|
| Аддитивті | + қосу | 0 – ноль | 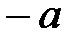 - қарама-қарсы - қарама-қарсы
|
Мультипликативті жағдайда топ аксиомалары мына түрде жазылады:
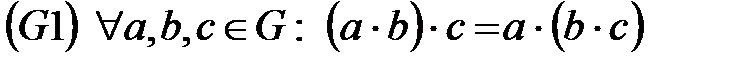 ,
,
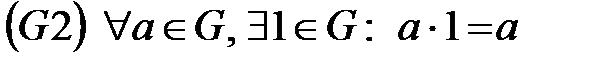 ,
,
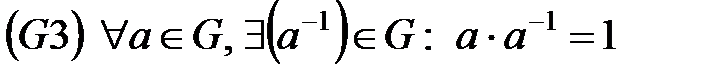 .
.
Мультипликативтік топтың қарапайым қасиеттері:
10. Бірлік элемент біреу ғана болады: 1 – біреу ғана;
20. Кез келген элементтің кері элементі біреу ғана болады: 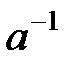 - біреу ғана;
- біреу ғана;
30. Кері элементтің керісі берілген элементтің өзіне тең болады: 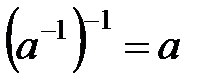 ;
;
40. Егер 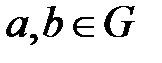 болса, онда
болса, онда 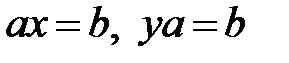 теңдеулері бір ғана шешімді болады;
теңдеулері бір ғана шешімді болады;
50. Егер 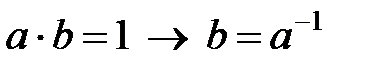 ; 60.
; 60. 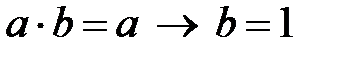 ;
;
70. 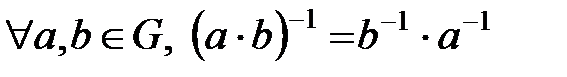 ;
;
80. а) 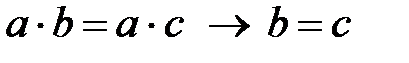 ; б)
; б) 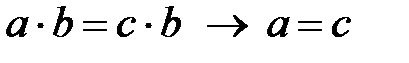 ;
;
90. Егер 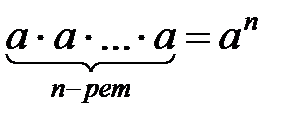 деп белгілесек, онда
деп белгілесек, онда 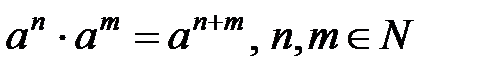 болады.
болады.
Аддитивті жағдайда топ аксиомалары мына түрде жазылады:
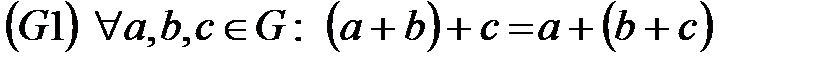 ,
,
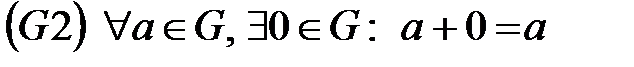 ,
,
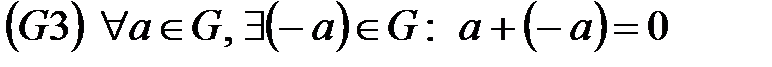 .
.
Абельдік топтар үшін 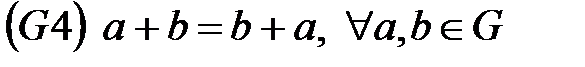 болады.
болады.
Аддитивтік топтың қарапайым қасиеттері:
10. 0 – біреу ғана; 20. 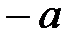 - біреу ғана;
- біреу ғана;
30. 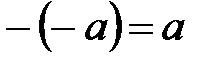 ;
;
40. 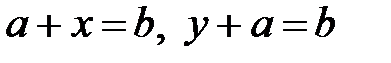 теңдеулерінің бір ғана шешімді болады;
теңдеулерінің бір ғана шешімді болады;
50. 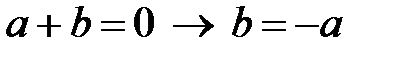 ; 60.
; 60. 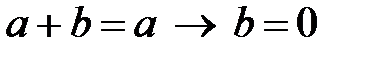 ;
;
70. 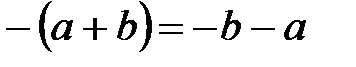 ;
;
80. а) 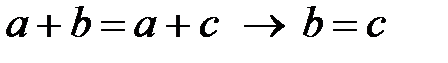 ; б)
; б) 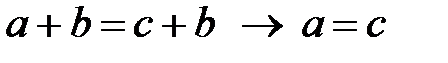 ;
;
90. 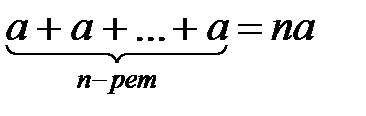 болады және
болады және 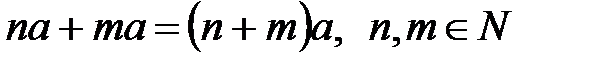 .
.
Ішкі топтар
Айталық 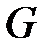 жиыны қандайда бір бинарлық амалға қатысты топ болсын.
жиыны қандайда бір бинарлық амалға қатысты топ болсын.
Анықтама. 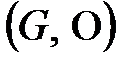 тобы үшін
тобы үшін 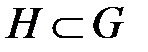 ішкі жиыны беріліп, ол
ішкі жиыны беріліп, ол 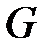 тобындағы амалға қатысты топ құрайтын болса, яғни
тобындағы амалға қатысты топ құрайтын болса, яғни 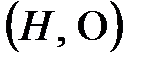 жүйесі топ болса, онда
жүйесі топ болса, онда 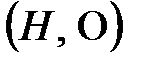 топты
топты 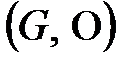 тобының ішкі тобы деп атайды.
тобының ішкі тобы деп атайды.
Мысал 2.1.8. 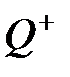 оң рационал сандар жиыны көбейту амалына қатысты топ құрайды, сондықтан ол оң нақты сандар мультипликативтік тобының ішкі тобы болып табылады.
оң рационал сандар жиыны көбейту амалына қатысты топ құрайды, сондықтан ол оң нақты сандар мультипликативтік тобының ішкі тобы болып табылады.
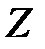 бүтін сандар жиыны қосу амалына қатысты топ құрайды және ол нақты сандар аддитивтік тобының ішкі тобы болып табылады.
бүтін сандар жиыны қосу амалына қатысты топ құрайды және ол нақты сандар аддитивтік тобының ішкі тобы болып табылады.
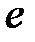 элемент
элемент 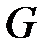 тобының бірлік элементі
тобының бірлік элементі 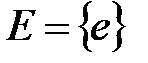 бір элементті жиын топ болады. Ол
бір элементті жиын топ болады. Ол 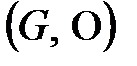 топтың ішкі тобы. Кез келген топты өзінің ішкі тобы деп қарастыруға болады.
топтың ішкі тобы. Кез келген топты өзінің ішкі тобы деп қарастыруға болады. 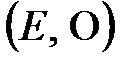 мен
мен 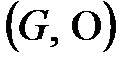 топтарын
топтарын 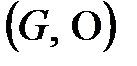 топтың айқын ішкі топтары деп атайды. Ал басқа ішкі топтарын айқын емес ішкі топ деп атайды.
топтың айқын ішкі топтары деп атайды. Ал басқа ішкі топтарын айқын емес ішкі топ деп атайды.
Ескерту. 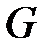 жиынның кез келген ішкі жиыны топ бола алмайды.
жиынның кез келген ішкі жиыны топ бола алмайды.
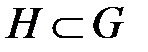 ішкі жиыны топ болуы үшін
ішкі жиыны топ болуы үшін 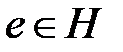 және
және
1) 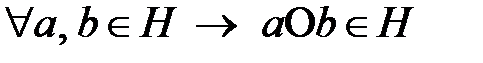 ;
;
2) 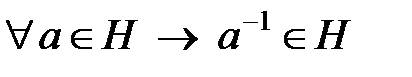 шарттары орындалуы керек.
шарттары орындалуы керек.
Сонымен, 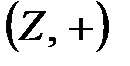 тобы
тобы 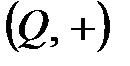 және
және 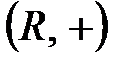 топтарының ішкі тобы болады.
топтарының ішкі тобы болады. 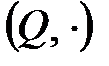 тобы
тобы 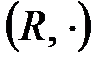 тобының ішкі тобы болады.
тобының ішкі тобы болады.
Мысал 2.1.9. 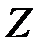 жұп сандар жиынын
жұп сандар жиынын 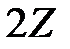 деп белгілесек.
деп белгілесек. 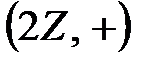 жүйесі
жүйесі 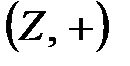 топтың ішкі тобы болады. 1) мен 2) шартты тексерсе жеткілікті.
топтың ішкі тобы болады. 1) мен 2) шартты тексерсе жеткілікті.
1) 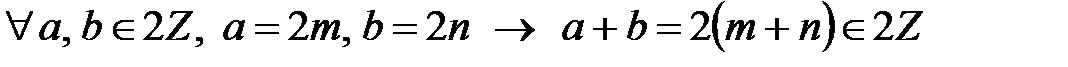 ,
,
2)  .
.
Ішкі топ болатын шартты қанағаттандырады.
Мысал 2.1.10. 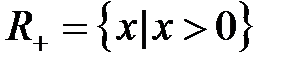 оң нақты сандар жиыны.
оң нақты сандар жиыны. 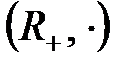 жүйесі
жүйесі 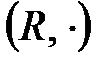 топтың ішкі тобы болады:
топтың ішкі тобы болады:
1) 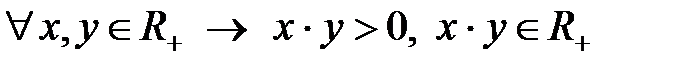 ,
,
2) 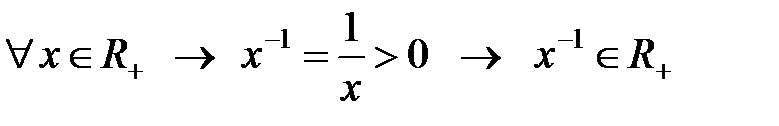 .
.
Ескерту. Тақ сандар жиыны 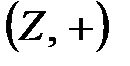 топтың ішкі тобы бола алмайды. Себебі екі тақ санның қосындысы мен айырмасы жұп сан болады. ■
топтың ішкі тобы бола алмайды. Себебі екі тақ санның қосындысы мен айырмасы жұп сан болады. ■
Дата добавления: 2016-04-02; просмотров: 4241;
