ЭПР құбылысының физикалық негіздері. g-фактор және оның қасиеттері

ЭПР спектроскопиясы әртүрлі химиялық мәселелерді шешуде кең қолданылады. Осы әдістің негізгі құндылығы – жұптаспаған электрондары бар бөлшектердің өте кіші концентрацияларын байқау, өлшеу және олардың энергиялық күйлері мен локализациясын сипаттауына мүмкіндік беретінімен байланысты. Үлгі осындай талдау әдісін қолданғанда бұзылмайды да, өзгермейді де. Жұптаспаған электрондары бар бөлшектер химиялық реакциялар өтетін жүйелерде өте маңызды роль атқарады, себебі, олардың химиялық активтігі өте жоғары. Сондықтан оларды байқау көп жағдайда реакция механизмін анықтауға жол ашады. ЭПР құбылысын Ресей ғалымы Е.К.Завойский 1944 жылы ашқан.

Жұптаспаған электрондары бар бөлшектерге кейбір атомдар, иондар, бос радикалдар, триплетті күйдегі молекулалар жатады, оларды екі топқа бөлуге болады:

1) жұптаспаған электроны бір атоммен байланысты: (Н, О, галоген атомдары, Feⁿ⁺, Coⁿ⁺, Nіⁿ⁺ ауыспалы элементтердің иондары, жартылай өткізгіштер);

2) жұптаспаған электрон бүтіндей молекуламен немесе оның үлкенірек бөлігімен байланысты (бос радикалдар, ион-радикалдар, триплетті-қоздырылған молекулалар), оның орбиталі бір жерде жинақталмаған.

g-фактор. Атомда бір жұптаспаған электроны бар, ядроның моменті нольге тең қарапайым жағдайды қарастырайық. Мұндай атомның магниттік қасиеттері жұптаспаған электронның орбиталдық магниттік және компенсацияланбаған спиндік магниттік моменттерімен анықталады. Орбиталдық моменттің жартылай классикалық моделі ретінде ядроның айналысында 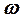бұрыштық жиілігімен айналатын заряды е электронды ұсынады, мұндай айналу магнит моментін тұғызатын 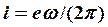айнымалы тоққа эквивалентті,

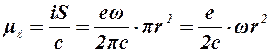(8.1)

мұндағы с – жарық жылдамдығы; r – электрон орбитасының радиусы; S – орбитамен қоршалатын аудан. Қозғалыс мөлшерінің механикалық моменті 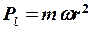, мұнда m – электронның массасы. Орбиталды магнит моментінің механикалық моментіне қатынасы (гиромагнитті қатынас) g_lнемесе орбиталдық магнетизмнің g-факторы (спектроскопиялық ыдырау факторы) деп аталады:

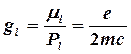(8.2)

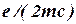бірлігінде 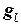=1 аламыз.

Квантты-механикалық қарастыру да орбиталдық 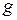-фактордың осы мәніне келтіреді. Шынында, кванттық механикаға сай, орбиталдық магниттік момент:

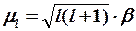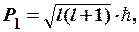және (8.3)

мұндағы l– орбиталық кванттық саны; 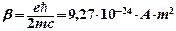– Бор магнетоны, оның мәні электронның орбиталдық магниттік моментінің кіші мәніне, яғни сутек атомындағы электронның бірінші Бор орбитасындағы моментіне тең; 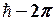-ге бөлінген Планк тұрақтысы. Осыдан:

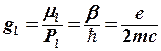(8.4)

Спиндік магнетизм үшін:

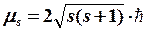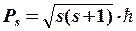және (8.5)

мұнда s-спиндік кванттық сан (электрон үшін s=1/2).

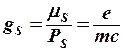(8.6)

яғни ( 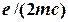бірлігінде) спиндік магнитизмнің 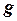-факторы 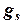=2 (дәлірек, релятивистік түзетуді ескергенде, бос электрон үшін Ланде 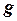-факторы тең болады 2,0023). Қазіргі әдебиетте 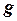-фактор өлшемсіз мән деп есептеледі, егер электронның магнит моменті Бор магнетонымен 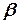, ал механикалық моменті 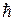бірлігінде өлшенген болса, оны (5.4) және (5.6) қатынастардан оңай табуға болады.

Спин-орбиталды байланыс бар кезде атомның толық магнит моменті құраушылардың екеуінің де векторлық қосындысының нәтижесі болып табылады, да 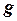-фактордың мәні аралық болады. Осы мәселені тереңірек қарастырайық. Бұл байланыс электронның спиндік магнит моментінің осы электронның орбиталды қозғалысының пайда болатын магнит өрісімен әрекеттесуінің нәтижесі болып табылады. Бір жұптаспаған электрон моделіне ядроның заряды Ze үшін әрекеттесу энергиясы:

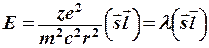(8.7)

Сонымен, Z өсуімен E өседі, орбиталді моментке және орбиталы түріне, яғни r радиусіне тәуелді. 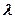-нің мәнін нақты атомдық жүйесі үшін оптикалық спектрлерінен табуға болады.

Жұптаспаған электрон S-орбитальде орналасқанда (l=0), оның магниттік де, механикалық та орбиталдық моменттері нольге тең. Онда .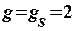

Бірақ, негізгі күйдің орбиталық деңгейлері энергия бойынша азғындаған болса, электрондардың орбиталық қозғалысы l ≠ 0 болса да 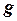-факторға ықпал етеді. Мысалы, р-электронның xy-жазықтықтағы орбиталық қозғалысын p_x-орбиталінен p_у-орбиталіне ауысуы ретінде қарастыруға болады (1-сурет).

Мұндай ауысу электронның энергиясы орбитальдің екеуінде де бірдей болғанда ғана мүмкін болады: E(p_x)=E(p_y), яғни азғындаған орбиталдер үшін мүмкін болады. Онда спиндік және орбиталдық моменттер өзара әрекеттеседі, жұптаспаған электрондардың күйі толық спиндік S және орбиталдық L моменттерімен және суммалық J моментімен бейнеленеді (мұнда J=L 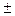S, таңба электрон қабықшаның толықтырылуы-на тәуелді). Бұл жағдайда 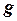-фактордың мәні 1 мен 2-нің арасында жатады да, газды фазадағы бос атомдар үшін Ланде формуласы арқылы есептеледі:

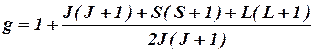(8.8)

Ланде формуласы жұптаспаған электрондар ішкі қабықшаларда орналасқанда, мысалы, сирек элементтердің иондары үшін орындалады. Мұндай электрондардың харктеристикасы, көп жағынан, ортамен әрекеттеспейтін, бос электрондардікіндей болады.

Егер парамагниттік бөлшектер оларды қоршайтын бөлшектерден пайда болса (мысалы, Cu және Fe тұздарында), орбиталдық азғындау жойылады да, 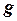-фактордың мәні 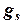=2, бұл жағдайда Ланде формуласын пайдалануға болмайды. Бірақ орбиталдардың энергия айырымы өте үлкен болғанда да, орбиталдық қозғалыстың ықпалы толық жойылмайды (бұл белгілі «туннель» эффектісіне негізделеді). Сонымен, 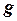-фактор спиндік мәніне тең болмайды, оны келесі формула арқылы есептеуге болады:

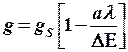(8.9)

мұнда 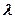– Рассел-Саундерстің спин-орбиталдық байланыс тұрақтысы, 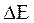– негізгі және оған ең жақын орбиталь күйлерінің энергия айырымы, а – парамагниттік бөлшектің табиғатын және бөлшектің магниттік моменті мен сыртқы магниттік өріс векторларының өзара бағытталуына тәуелді көбейткіш.

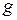-фактордың анизотропиясы. Магнит өрісі әртүрлі бағытталғанда орбиталды қозғалысқа әртүрлі орбиталдар қатысады да, 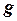-фактордың мәні магниттік өрістің бағытына тәуелді болу керек. Бұл құбылыс 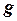-фактордың кеңістік анизотропиясы деп аталады. Оны нитроксил радикалының >N-O* фрагменті мысалында қарастырайық. Индукциясы В сыртқы магнит өрісі x осіне параллелді, ал жұптаспаған электрон оттек атомының p_z-орбиталінде орналасқан болсын, бұл уz жазықтығындағы орбиталды қозғалысқа келтіреді (2-сурет).

Бұл қозғалысқа оттек атомының бөлінбеген қос электроны орналасқан p_y-орбиталі де қатысу керек. yz жазықтықтағы орбиталді қозғалысты қос электронның біреуінің орбиталға ауысу ретінде қарастыруға болады, осы себептен n 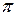^ж -қозу энергиясы деңгейлердің 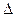Е бөліну мәнінің бағалауы болып табылады. Онда, (5.9)-формулаға сәйкес, табамыз:

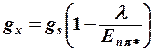(8.10)

Егер В индукция у-осіне параллелді болса, орбиталды қозғалысқа N-O байланыстың s-орбиталі қатысады, онда 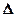Е 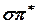-аусудың энергиясына тең, және :

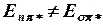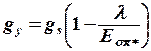(8.11)

Егер В индукция z-осіне параллелді болса, жұптаспаған электронның орбиталді қозғалысы болмайды да, g_z=g_s. Сонымен, 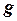-фактордың кеңістік анизотропиясының маңызы – оның мәні В индукцияның бағыты мен молекулалық осьтерінің арасындағы бұрыштарына тәуелді. Жалпы жағдайда:

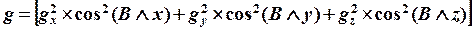(8.12)

мұнда g - екінші рангты тензор; g_X, g_Y, g_Z - оның негізгі мәндері.

Жиі кездесетін жағдай – 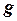-ның екі негізгі мәні бір біріне тең (аксиалды-аназотропты фактор), мысалы, 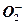ионында осы жағдай орындалады. 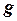-фактордың анизотопиясы ЭПР спектрлерінде өзгеше байқалады.

Сыртқы тұрақты магнит және айнымалы электр магнит өрістеріндегі парамагнитті бөлшектер. Парамагниттік бөлшектің сыртқы тұрақты магнит және айнымалы электр магнит өрістеріндегі тәртібін қарастырайық.

Сыртқы магнит өрісі жоқ кезде жұптаспаған электрондардың магниттік моменттері бейберекет бағытталады. Сыртқы тұрақты магнит өрісінде электрондар реттеледі. Квантталу шарттары бойынша электронның магниттік моментінің бағыттарының саны (2s+1)-ге тең. Электронның спині s=1/2, осыған сәйкес моментінің 2 бағыты болуы мүмкін: өріс бойымен (магниттік кванттық саны m_S=-1/2) және оған кері (m_S=+1/2). Өріс z-осі бойынша бағытталған болса, яғни ћ бірлігі квант санына m_s тең болатын электронның толық механикалық моменті 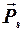орнына оның проекциясын 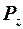есепке алу керек, электронның магниттік моменті пен сыртқы магнит өрісі В-нің өзара әрекеттесу энергиясы үшін былай жазуға болады:

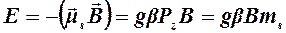(8.13)

Магниттік моменттің өріс бойымен параллельді бағытталуы (m_S1=-1/2) өріске кері бағытталуына (m_S2=-1/2) энергиясы жағынан пайдалы, сондықтан оған электронның төмен энергиясы сай болады. Демек, тұрақты магниттік өрісте барлық парамагниттік бөлшектер энергиясы әртүрлі екі топқа бөлінеді, сонымен, өрісте азғындау жойылады да, екі Зееман энергия деңгейлері пайда болады. Олардың энергия айырымы келесі теңдеумен бейнеленеді:

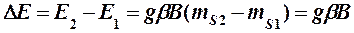(8.14)

Тепе-тендік күйде Больцман таралуы бойынша бөлшектің энергиясы exp(-E/kT)-ге пропорционалды. Төменгі E₁ деңгейде спиндер өріске кері бағытталған (яғни моменттері өріс бойымен), бұл деңгейдің толықтырылуы былай жазылады:

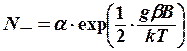(8.15)

жоғарғы Е₂ деңгейдің толықтырылуы:

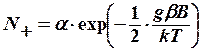(8.16)

Тепе-теңдіктегі толықтырылу қатынасы

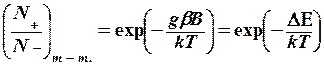(8.17)

Әдетте В=0,3 Тл, Т>10 К, 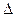E <<kT.

Соңғы теңдіктегі экспонентаны қатарға жіктеп табамыз:

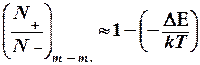(8.18)

мұндағы, N = N₊ + N_- – парамагниттік бөлшектердің толық саны, n₀=(N₊+N_-)_т-т – тепе-теңдіктегі деңгейлердің толықтырылу айырымын белгілеп, және n₀>>N₊,N_- ескере отырып, табамыз:

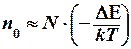(8.19)

Тұрақты магнит және айнымалы электр магнит өрісіндегі парамагниттік бөлшектер. ЭПР шарттары. Байқалатын тепе-теңдік – динамикалық тепе-теңдік болып табылады, яғни электрондардың жоғарғы деңгейден төменгісіне және кері ауысу жиіліктері жуықтап алғанда бірдей болады. Егер үлгіге жиілігі 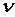айнымалы электр- магнит өрісімен әсер етсе, онда айнымалы өрістің кванты 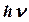болған жағдайдағы зееман деңгейшелерінің энергия айырымы :

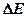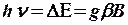(8.20)

электрондар төменгі деңгейден айнымалы өрістің энергиясын жұтып (резонанстық жұту), жоғарғы деңгейге ауыса бастайды. Мұндай энергия жұтуымен өтетін мәжбүр (индуцирленген) ауысулардың сипаты резонансты болады, яғни электрмагниттік сәулелердің белгілі жиілігінде байқалады. Басқа жиіліктерде мәжбүр ауысулардың ықтималдығы тез төмендейді.

Осы ауысулармен қатар жоғарғы деңгейден төменгі деңгейге энергия шығарумен кері ауысулар да өтеді. Энергиясы төмен күйлер энергетика жағынан пайдалы болғандықтан қоздырылған күйдегі электрондардың саны N₊ қоздырылмаған электрондардың санынан N_- 0,2% кіші болғандықтан, төменгі деңгейден жоғары деңгейге энергияны жұтумен өтетін ауысулар басым болады, яғни айнымалы өрістің резонанстық энергия жұтуы суммалы түрде орын алады. Бұл құбылыс – ЭПР құбылысы – резонанстық жиілігі бар айнымалы өрістің әсерінен электрондардың бір деңгейден басқа деңгейге ауысуы (3-сурет) болып табылады. Резонансқа магнит өрісінің индукциясын В немесе айнымалы электро-магниттік өрістің жиілігін 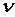өзгерту арқылы жетуге болады. Практика жүзінде индукцияны өзгерту ыңғайлы.

Ауыспалы өрістің магнитті векторы тұрақты өріс индукциясының векторына перпендикулярлы болғанда максималды жұтылу байқалады. Резонанстық жұтуда таңдап алу ережесі 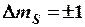орындалу керек. ЭПР спектрі электромагниттік сәуленің жұтылған қуатының (І_ж) тұрақты магнит өрісінің индукциясына (B) тәуелділігін береді. Резонанс жағдайы әдетте g=hν/(bB) сипатталады.

Белгілі энергия деңгейінен уақыт бірлігінде босатылған бөлшектердің саны деңгейдің толықтырылуына пропорционалды. ЭПР байқалатын кезде бейберекет (спонтандық) ауысулардың ықтималдығы кіші, ал екі жаққа да өтетін мәжбүр ауысулардың ықтималдықтары бір-біріне тең:

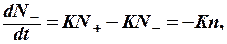(8.21)

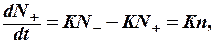(8.22)

мұнда К – мәжбүр ауысулардың ықтималдығы, кванттық механикаға сәйкес айнымалы өрістің қуатына пропорционалды, n=N_--N₊ – толықтырулардың айырымы.

Ауыспалы өріс қуаттылғының өсуі екі жақтың да ауысулар жылдамдығын арттырады. Релаксацияны ескермеген жағдайда 8.21-теңдеуден 8.22-теңдеуді алып тастап, келесі теңдеуді аламыз:

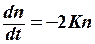(5.23)

t=0 кезінде n=n₀ деп есептеп, (5.23)-тен табылады:

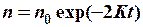(8.24)

яғни, релаксация процестері жоқ кезде ұзақ уақыт аралығында (t 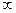) деңгейлердің толықтырылуы теңеседі (n 0). Айнымалы өрістің жұтылатын қуаты:

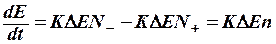(8.25)

яғни, деңгейлердің толықтырылуы теңескеннен кейін айнымалы өріс энергиясының жұтылуы тоқтатылады да, резонанстық жұту жоғалады. Бұл құбылыс қанығу деп аталады.