Лекция №3. Антеннаның бағытталған және поляризациаланған қасиеттерін сипаттайтын параметрлер.

Лекция жоспары:

· антеннаның бағытталу сипаттамасы (диаграммасы);

· қарапайым вибратордың және күрделі антеннаның бағытталау диаграммалары;

· сызықты поляризацияланған өрісті сәулелейтін антенналар үшін бағытталау диаграммалары;

· нақты антеннаның бағытталу диаграммасы.

Антеннадан электромагниттік өрісі сәулеленгендегі есебін көп кәдімгі қорек көздерінен (сәулеленгіштер) тұратын құрылғы ретінде қарастырған жөн. Максвеллдің сызықтық теңдеуінің арқасында кәдімгі қорек көзі поляларына суперпозиция принципі қолданылуы мүмкін. Ол оның кәдімгі сәулеленгіштерінен тұратын поляларын соммалау нәтижесінде антеннаның полясын табуға мүмкіндік береді. Поляларды соммалау қорек көздері бойынша олардың интегралдауына алып келеді. Кәдімгі қорек көздеріне мыналар жатады: сымды антенналар болған жағдайларда кәдімгі электрлі вибраторлар КЭВ; щелдік антенналар болған жағдайда кәдімгі магнитті вибраторлар; апертурлы антенналар болған жағдайларда толқынды фронттың шексіз кіші элементтері немесе Гюйгенс элементтері.

Электромагниттік поляның векторлық сипатының есебінсіз алыс аймақтағы еркін шынайы антеннаның Е электрлік поляның кернеулілігінің комплексті амплитуда үшін формуласы мынадай түрде болады:

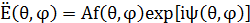(3.1)

мұндағы: А – бағытталудан бақылану нүктесіне байланысты емес комплексті көбейткіш (оған стандартты көбейткіш exp(-ikr)/r, мұндағы r – антеннаның фазалық орталығынан бақылау нүктесіне дейінгі арақашықтық болып табылады; 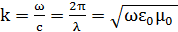- фаза коэффициенті немесе еркін кеңістіктегі толқындық сан); θ,φ – бақылау нүктесінің координаттары; |f(θ,φ)| - бағытталудың амплитудалық сипаттамасы; ψ(θ,φ) – бағытталудың фазалық сипаттамасы. Кәдімгі электрлік вибратор жағдайында:

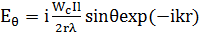(3.2)

мұндағы: I – вибратордағы токтың амплитудасы; l – вибратордың ұзындығы; 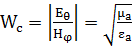толқынның сипаттамалық кедергісі; еркін кеңістікте 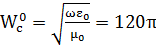Ом.

Антеннаның бағытталуының амплитудалық сипаттамасы деп кернеулік шамасының (модуль) электрлік поляға тәуелділігін айтамыз. Ол бағытталудан осы нүктеге дейін тұрақты арақашықтықта θ бұрыштары мен φ координатаның сфералық жүйесімен сипатталатын антеннадан бақылау нүктесіне дейінгі бақылау нүктесінде антеннамен жасалады. Антеннаның бағытталуының фазалық сипаттамасы деп θ және φ бұрыштарымен сипатталатын, бақылау нүктесінде антеннамен жасалған, алыс зонада сфераның бетінде орналасатын, бағытталудан осы нүктеге дейінгі поля фазасының тәуелділігін айтамыз. f(θ,φ) көбейткіш шаманы ғана анықтап қоймай, сонымен қатар поляның кернеулік фазасын анықтайды, өйткені 180^º -қа поляның кернеулік фазасынының секіруіне сәйкес келетін f(θ,φ) функциясы нөл арқылы ауысқанда оның белгісі өзгереді. Сондықтан, бағытталудың амплитудалық сипаттамасы осы функцияның |f(θ,φ)| модулі болып табылады. Ары қарай жазуды оңайлату үшін модулдің белгісін жазбай отырамыз. Жалпы жағдайда бағытталудың сипаттамасы векторлық және комплекстік шама болып табылады. 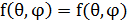, 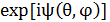көрінісі деп антеннаның бағытталуының комплексті сипаттамасын айтамыз. Ол антеннаның алыс зонасында электромагниттік полядан сәулеленетін бұрыштық таралу мен фазалық қасиеттерін толық анықтайды. Антеннаның бағытталу сипаттамасы антеннаның өлшемдерімен және конфигурацияларымен, сондай-ақ қозған токтың таралуымен анықталады. Еске сала кетсек, алыс зона (сәулелену зонасы немесе Фраунгофе-ра зонасы) осы зонада орналасқан антеннаның кез келген нүктесінен бақылау нүктесіне жүргізілген сәуленің бағытталуы параллельді болады деп сипатталады. Әйткенмен, антеннаның әртүрлі элементтерімен бақылау нүктесінде жасалатын поляның фазасын анықтауда қате табылады. Антеннаның өлшемдерімен салыстырғанда антеннамен бақылау нүктесінің арақашықтығы артқан сайын бұл қате азая береді. Алыс зонаның rизл арақашықтығы rизл ≥2R²/λ шартымен анықталады, мұндағы R – сәулелегіш жүйенің ең үлкен өлшемі. Бұл зонада поляның көлденең сипаттамасына ие болады (таралу бағытында жасаушы Е және Н векторлары болмайды); бақылау нүктесінің айналасында поля тегіс толқын сипаттамасына ие болады; антенна элементтерімен сәулеленетін поляның амплитудалары кері пропорционалды арақашықтықты жоқ қылады.

Әдетте, өрістің абсолютті кернеу шамасына емес, антенна техникасында бағытталудан бақылау нүктесіне дейінгі кернеу тәуелділігі сипаттамасына көңіл бөледі. Сондықтан, бағытталудың нормаланған сипаттамасын F(θ,φ) қолданған ыңғайлы, яғни максималды сәулелену бағытында кернеулік белгісіне еркін бағытта антеннадан сәулеленетін поля кернеулілігінің ара қатынасы болып табылады F(θ,φ) = |E(θ,φ)|/|Emax(θo,φo)| = f(θ,φ)/fmax(θo,φo).

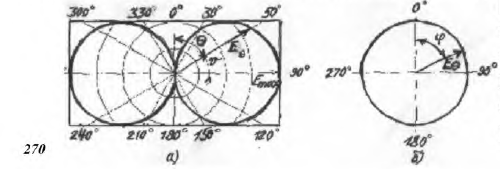
F(θ, φ) максималды шама әрдайым бірге тең. Бағытталудың амплитудалық сипаттамасының графикалы көрінісін антеннаның бағытталу диаграммасы (БД) деп атайды. Кеңістіктік БД ұзындығы анықталған масштабта әр бағытта f(θ,φ) функциясына тең болатын, координатаның басынан шығатын, радиус-векторы соңымен көрінетін, f(θ,φ) немесе F(θ,φ) беткі қабаты түрінде суреттеледі. 3.1а суретте кәдімгі вибратордың (тороид) кеңістіктік БД-сы бейнеленген, 3.1б суретте күрделі антеннаның БД-сы бейнеленген.

а) 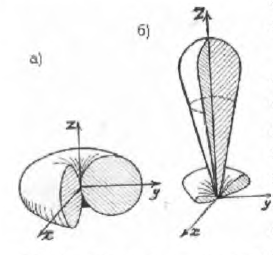б)

Сурет 3.1 - Жазықтықты БД (а-Герц диполі, б-инелі)

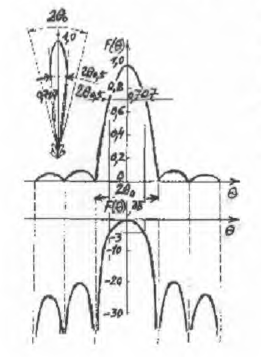
Негізі тәжірибиеде қандайда бір таңдалған жазықтықтағы бағытталу сипаттамасын бейнелейтін БД-ны қолданады. Мұндай жазықтықтар ретінде негізі максималды сәулелену бағыты арқылы сәйкес келетін, екі өзара перпендикуляр жазықтықтар таңдалады. Сызықты поляризацияланған поляны сәулелейтін антенналар үшін негізгі жазықтықтар деп Е немесе Н векторларында (жазықтықта) жататын жазықтықты айтады. Бағытталу диаграммалары полярлық (сурет 3.2а – Е жазықтықтағы кәдімгі вибраторлы БД; сурет 3.2б – Н жазықтықтағы кәдімгі вибраторлы БД) немесе декарттық (тікбұрышты) координата жүйелерінде (сурет 3.3 – нақтылы антеннаның БД-сы) бейнеленеді.

Сурет 3.2 – Герц диполінің БД-сы (а-Е жазықтық, б-Нжазықтық)

Кейбір жағдайларда жазықтықтық (үш өлшемді) БД-ны бейнелейтін картографиялық тәсіл қолданылады. Ол бұрыштардың үлкен диапазонында көп желекті (яғни көп нөлдері мен максимумдары бар) БД-ны бейнелеу үшін ыңғайлы. Бұл тәсіл географиялық картадағы меридиандар мен паралллелдер торы сияқты қандай да бір координаталық жүйеде θ φ координатасының тегіс сеткасы құрастырылуынан құралады. Осы торда бекітулі сызық ретінде әр түрлі масштабтағы F(θ,φ) нөмірленген бағытталу сипаттамасының бірдей мағынасын бейнелейді. БД-ны бейнелеу үшін, көбінесе, F(θ,φ)=20lg F(θ,φ) децибелл арақатынасымен енгізілетін логарифмдік масштаб қолданылады.

Кейбір жағдайларда F²(θ,φ) қуатындағы бағытталу сипаттамасы (диаграммасы) ұғымы қолданылады. F(θ,φ) функциясы θ және φ әртүрлі бұрыштары үшін нөл арқылы өтеді және бірнеше максимумдері болады, яғни БД-ның көп желекті сипаттамсы болады. Бағытталу диаграммасын бас желектің енімен (сәуле ені) және бүйір желектің салыстырмалы деңгейімен сандық жағынан сипаттау үйреншікті.

Сурет 3.3 - Нақтылы антеннаның БД-сы

БД ені (сәуле ені) деп поля кернеуі белгілі бір мәнге дейін түсетін, бағытталулар арасындағы бұрышты айтамыз. Осылай нөлдік сәулелену деңгейі бойынша БД енін поля кернеуі нөлге дейін түсетін (сурет 3.3) бағытталулар арасындағы 2θ0 бұрышын айтады. Қуат жартысы бойынша БД ені деп |Е|=|Emax|/√2 немесе 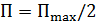қуат ағынының орташа тығыздық мәніне сәйкес бағыттаулар арасындағы 2θ0,5 бұрышын айтамыз. Максималды сәулелену бағытына сәйкес максимумды ең үлкен желекті бас желек деп , ал кіші желектерді бүйір (артқы квадрантта орналасатын желектер, яғни 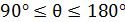және 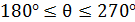бұрыш диапазондарында орналасатын желектер, оларды көбіне артқы деп атайды) деп атаймыз.

Салыстырмалы бүйір желек деңгейіде (БЖД) берілген желекте (ENmax) максимум бағытындағы полясы, кернеуі бас максимум (Emax) бағытында поля кернеуіне қарай ара қатынасы болады, яғни 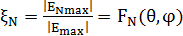, немесе децибеллда 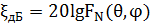, мұндағы N=1,2,3,.....- бүйір желек нөмірі (бас желек үшін N=0).

Әдетте, бүйір желекті басуға ұмтылады, яғни 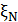шамасы аз болуына ұмтылу. Көп жағдайда бағытталудың амплитудалық сипаттамасына көңіл бөледі. Бағытталудың фазалық сипатамасын радиолокацияда, радионавигацияда және басқа да бірқатар жағдайларда қолданады.

Егер поля антеннасынан сәлеленетін фаза бағытталудан бақылау нүктесіне байланысты болмаса және тек f(θ,φ) немесе F(θ,φ) функциялары нөл арқылы өткенде керіге өзгереді, яғни БД-ның бір желектен екіншісіне өтсе, онда мұндай антенна сфералық толқынның қорек көзі болып табылады. Оған 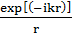көбейткіші дәлел бола алады. Бұл толқындар антеннаның фазалық орталығы деп аталатын бір нүктеден таралады. Бұл нүкте таңдалған координата жүйесінің басында орналасқан, сондықтан фазалық сипаттама координата бастауының орналасуына байланысты болады. Бірақ барлық нақты антенналардың фазалық орталығы болмайды, яғни сфералық толқындарды сәулелейді. Әдетте оларға толқын фронтын ең жақсы аппроксимациялайтын сфераны таңдап алуға болады. Осы сфераның орталығын антеннаны сәулелейтін орталығы деп атайды. Фазалық сипаттаманың графикалық бейнесі деп фазалық БД-ны айтады.

Бақылау сұрақтары:

1. Антеннаның бағытталуының амплитудалық сипаттамасы дегеніміз не?

2. Бағытталау диаграммасы дегеніміз не?

3. Бағытталу ені (сәуле ені) дегеніміз не?

Лекция №4. Бағытталған әрекет коэффициенті, антеннаның күшейту коэффициенті және бағытталған әрекет коэффициентімен байланысты параметрлер.

Лекция жоспары:

· антенналардың электромагниттік өрістерді топтау қасиеттері;

· антеннаның күшейту коэффициенті;

· бағытталау коэффициентіне қатысты басқа параметрлер.

Бағытталған әрекет коэффициенті (БӘК) антеннаның қандай да бір анықталған бағытта сәулеленген электромагниттік өрістің топтау қабілеттілігін сипаттайды. Бұл ұғым 1929 жылы А.А.Пистолькорспен енгізілген болатын. Бағытталған әрекет коэффициенті деп берілген бағытта П (θ1,φ1) антеннадан сәулеленетін қуат ағыны тығыздығының жоғары жиілік кезеңінде орташа мәні мен қуат ағыны тығыздығы мәнінің Пуср барлық бағыттардағы орташаландырылған мәні арасындағы қатынасты айтамыз.

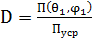(4.1)

Мұнда 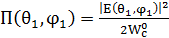, мұндағы 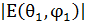- θ₁, φ₁ бұрыштарымен сипатталатын бағыттағы электрлік поля кернеуінің амплитудалық мәні. Осылайша, БӘК-ті анықтағанда берілген антенна осы антенна сәулелейтін қуатты сәулелейтін, жорамалдағы мүлде бағытталмаған (изотропты) антеннамен салыстырылады.

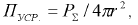(4.2)

мұндағы: Р_Σ - сәулелену қуаты, r – антеннаны қамтитын жорамалдағы сфераның радиусы, сонымен қатар r шамасы сфераның беткі қабаты антенна полясының алыс зонасында орналасуын талап етеді.

Бағытталған әрекет коэффициент изотропты (бағытталмаған) антеннадан бағытталған антеннаға ауысуы кезінде, бақылыу нүктесіндегі орташа мәндегі қуат ағынының тығыздығы өзгеріссіз қалуы үшін сәулеленген қуатты қанша рет азайту керектігін көрсетеді.

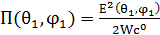ескеріп, (4.2) мәнін (4.1) қоя отырып, БӘК үшін басқа түрдегі келесі формуланы аламыз 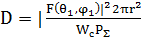немесе максимальді сәулелену бағытындағы ( 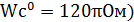бос кеңістік үшін.

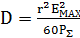(4.3)

Егер осы формулаға 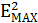орнына (4.1) мәнін квадраттап, ескереміз 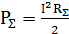, мұндағы 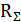- элементар электрлі вибратордың сәулелену кедергісі, онда элементар вибратордың БӘК аламыз D=1,5.

Кеңістіктік ДН басты күлтесі жіңішкерген сайын және УБЛ кішірейген сайын БӘК үлкейеді. БӘК әрекет етуші ұзындық немесе антеннаның әрекет етуші биіктігі 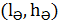деп аталатын параметрмен білдіруге болады. Бұл параметр кейде қабылдаушы антеннаны талдаған кезде, ұзынтолқынды және орташатолқынды сымды антеннада және мачт-антеннада қолданылады.

Желілі антенна жағдайында ток оның ұзындығы бойынша таралмаған. Алайда шынайы антеннаны басты бағыттағы антенна өрісіне тең максимальді сәулелену өрісі бағытында туатын біркелкі таралатын токпен, ұзындығы 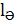болатын ойдағы вибратормен ауыстыруға болады. Бұл бойынша шынайы антеннаның қоректену нүктесіндегі ток ойдағы вибратор бойынша ағатын токқа тең. Ұқсастық бойынша басты бағыттағы шынайы антеннаның кернеу өрісін келесі түрде көруге болады

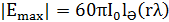(4.4)

мұндағы: 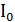- антеннаның қоректену нүктесіндегі ток амплитудасы; 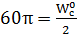, мұндағы 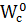- ортаның толқындық кедергісі. Ерікті бағыттағы кез келген вибраторлы антеннаның кернеу өрісінің шамасы үшін келесі формуланы жазамыз:

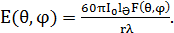(4.5)

(4.3) Формуладағы 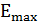орнына (4.4) мәнін қоя отырып, ескереміз 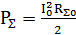( 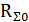- қоректену нүктесіндегі токқа қатысты антеннаның сәулелену кедергісі; І- антеннаның қоректену нүктесіндегі ток) және келесі формуланы аламыз:

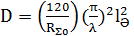немесе (4.6)

Шамалы өлшеммен «нақты ұзындық» кез келген антеннада қолдануға болады. Бұл өлшем БӘК арқылы көрініс табады, ал соңғысы тек қана бағыттылықтың сипаттамасымен анықталады.

Антеннаны қоршаған заттарда, изоляторда және жерде БӘК антеннаның өткізгішінде энергия жоғалысын (потерь) есептемейді. Осыған байланысты антеннаның күшейткіш коэффициенті (КК) деп аталатын жоғалысты есептейтін өлшем жүргізіледі. Осы бағыттағы сәулеленген антеннаның орташа мәндегі қуат ағыны тығыздығының 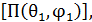ойдағы абсолютті бағытталмаған сәулелегіш тудыратын орташа мәндегі қуат ағынының тығыздығы ( 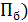қатынасына тең. Бақылау нүктесінен қарағанда екі антенна бірдей арқашықтықта орналасқан; басқа антеннаға жүргізілген қуатта тең және бағытталмаған антеннаның БӘК бірлікке тең. Олай болса КК.

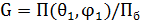. (4.7)

Абсолютті бағытталмаған антеннамен салыстырғанда күшейткіш коэффициент бағытталған антеннаға қуаттың қанша рет азайту керектігін көрсетеді. Орташа мәндегі қуат ағынының тығыздығы бақылау нүктесінде өзгеріссіз қалуы үшін ПӘК бірлікке тең деп есептеледі.

КК анықтау барысында оның БӘК айырмашылығы осы антенналардың сәулелену қуатының теңдігіне емес, жүргізілген зерттеулерде және эталонды антеннада, яғни қуат теңдігінен шығуында. Көбейтіп, оң бөлігін (4.7) 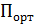бөлеміз.Сонда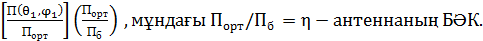

Параметрлер (D, G және η) келесі арақатынаспен байланысты

G=Dη (4.8)

D=G/η ескере отырып, былай жазуға болады

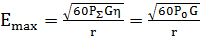(4.9)

Бақылау сұрақтары:

1. Антеннаның бағытталу әрекет коэффициені дегеніміз не?

2. Антеннаның күшейту коэффициенті нені есептейді?

3. Антеннаның күшейту коэффициенті және БӘК-пен байланысты параметрлер?