Бейтарап (нейтрал) және кері элементтер. Кері амалдар
Айталық 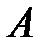 жиынында бинарлық амал берілсін.
жиынында бинарлық амал берілсін.
Анықтама. Егер кез келген  элементі үшін
элементі үшін 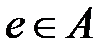 элементі табылып
элементі табылып
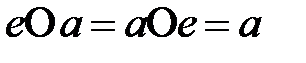
теңдігі орындалатын болса, онда 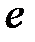 элементі берілген амалға қатысты бейтарап (нейтрал) элемент деп аталады.
элементі берілген амалға қатысты бейтарап (нейтрал) элемент деп аталады.
Мысал 2.1.4. 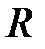 жиынында 1 саны көбейту амалына қатысты бейтарап элемент,
жиынында 1 саны көбейту амалына қатысты бейтарап элемент, 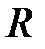 жиынында 0 саны қосу амалына қатысты бейтарап элемент, ал екінші ретті нөлдік матрица – екінші ретті барлық матрицалар жиынында матрицаларды қосу амалына қатысты бейтарап элемент болып табылады. Басқаша жағынан,
жиынында 0 саны қосу амалына қатысты бейтарап элемент, ал екінші ретті нөлдік матрица – екінші ретті барлық матрицалар жиынында матрицаларды қосу амалына қатысты бейтарап элемент болып табылады. Басқаша жағынан, 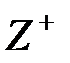 бүтін оң сандар жиынының
бүтін оң сандар жиынының 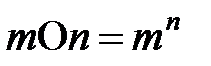 формуласымен берілген амалға қатысты бейтарап элементі жоқ.
формуласымен берілген амалға қатысты бейтарап элементі жоқ.
Бұл мысалдар, бейтарап элементтің жалғыз болуы немесе мүлдем болмауы мүмкін екенін көрсетеді.
Айталық 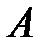 жиынының қандай да бір бинарлық амалға қатысты
жиынының қандай да бір бинарлық амалға қатысты 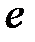 бейтарап элементі бар болсын.
бейтарап элементі бар болсын.
Анықтама. 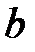 элементі
элементі 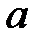 элементі үшін кері элемент деп аталады, егер
элементі үшін кері элемент деп аталады, егер
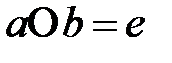 және
және 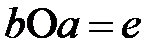
теңдіктері орындалатын болса.
Анықтамадан, егер 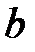 элементі
элементі 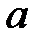 элементі үшін кері элемент болса, онда
элементі үшін кері элемент болса, онда 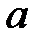 элементі
элементі 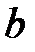 элементі үшін кері элемент болып табылатыны шығады.
элементі үшін кері элемент болып табылатыны шығады.
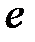 бейтарап элементі өзіне өзі кері элемент болады, оның басқадай кері элементтері болмайды.
бейтарап элементі өзіне өзі кері элемент болады, оның басқадай кері элементтері болмайды.
Мысал 2.1.5. 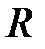 жиынындағы көбейту амалына қатысты (бейтарап элементі 1 саны болып табылады) нөлден өзгеше кез келген
жиынындағы көбейту амалына қатысты (бейтарап элементі 1 саны болып табылады) нөлден өзгеше кез келген 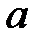 элементі үшін кері элемент
элементі үшін кері элемент 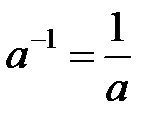 саны болып табылады және ол біреу ғана болады.
саны болып табылады және ол біреу ғана болады.
0 санының кері элементі жоқ, өйткені ешқандай 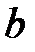 саны үшін
саны үшін 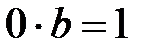 теңдігі орындалмайды.
теңдігі орындалмайды.
Егер көбейту амалын тек 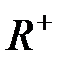 оң нақты сандар жиынында қарастырсақ, онда барлық элементтердің бірден-бір кері элементтері бар болады.
оң нақты сандар жиынында қарастырсақ, онда барлық элементтердің бірден-бір кері элементтері бар болады.
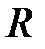 жиыны қосу амалына қатысты (бейтарап элементі - 0 саны) жүйе болып табылады, оның әрбір
жиыны қосу амалына қатысты (бейтарап элементі - 0 саны) жүйе болып табылады, оның әрбір 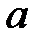 элементінің бір
элементінің бір 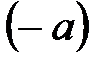 кері элементі бар:
кері элементі бар: 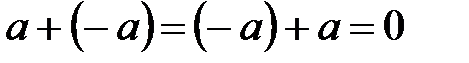 .
.
Екінші ретті матрицалар жиынында матрицалық көбейту амалына қатысты (бейтарап элемент – бірлік матрица) әрбір азғындалмаған 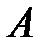 матрицасы үшін жалғыз ғана кері элемент -
матрицасы үшін жалғыз ғана кері элемент - 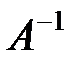 матрицасы бар болады, өйткені:
матрицасы бар болады, өйткені: 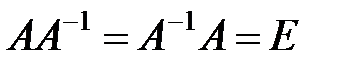 , бірақ ешқандай азғындаған матрицаның кері элементі болмайды.
, бірақ ешқандай азғындаған матрицаның кері элементі болмайды.
Кері элемент ұғымымен кері амал ұғымы тығыз байланысқан.
Анықтама. 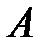 жиынындағы амал кері амал деп аталады, егер
жиынындағы амал кері амал деп аталады, егер 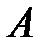 жиынының
жиынының 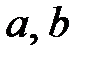 элементтері үшін әрбір
элементтері үшін әрбір
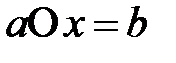 және
және 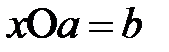
теңдеулерінің жалғыз бір ғана шешімдері бар болса.
Мысал 2.1.6.Барлық 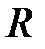 нақты сандар жиынында (сонымен қатар барлық
нақты сандар жиынында (сонымен қатар барлық 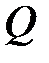 рационал сандар жиынында немесе барлық
рационал сандар жиынында немесе барлық 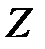 бүтін сандар жиынында) қосу амалының кері амалы бар, ал бүтін теріс емес сандар жиынында кері амалы жоқ (егер
бүтін сандар жиынында) қосу амалының кері амалы бар, ал бүтін теріс емес сандар жиынында кері амалы жоқ (егер 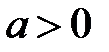 болса, онда
болса, онда 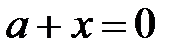 теңдеуінің бүтін теріс емес шешімі болмайды).
теңдеуінің бүтін теріс емес шешімі болмайды).
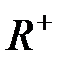 жиынында көбейту амалының кері амалы бар, бірақ
жиынында көбейту амалының кері амалы бар, бірақ 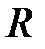 жиынында кері амалы жоқ, өйткені
жиынында кері амалы жоқ, өйткені 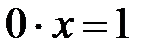 теңдеуі шешілмейтіндік болып табылады.
теңдеуі шешілмейтіндік болып табылады.
Дата добавления: 2016-04-02; просмотров: 2557;
