Сақинаның қарапайым қасиеттері

Теорема. 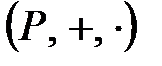сақинасы үшін мына қасиеттер орындалады:

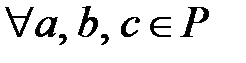элементтері үшін

1⁰. 0 элемент біреу ғана; 2⁰. ;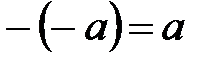

3⁰. 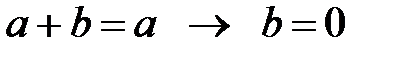; 4⁰. ;

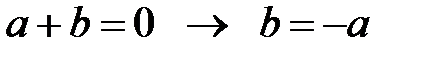5⁰. 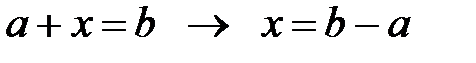; 6⁰. а) ,

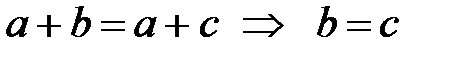б) ;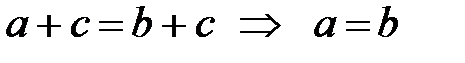

7⁰. 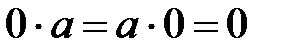; 8⁰. ;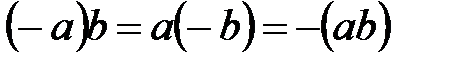

9⁰. 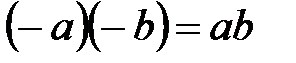; 10⁰. ;

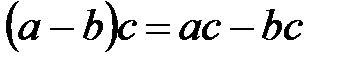11⁰. .

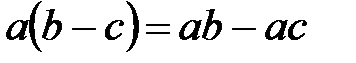Дәлелдеуі. 1⁰ - 6⁰ қасиеттер топтың қасиеттерінен белгілі.

7⁰. .

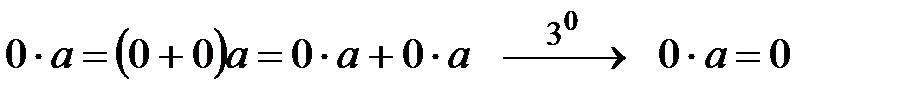Осымен бірдей 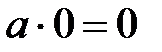дәлелденеді.

8⁰. 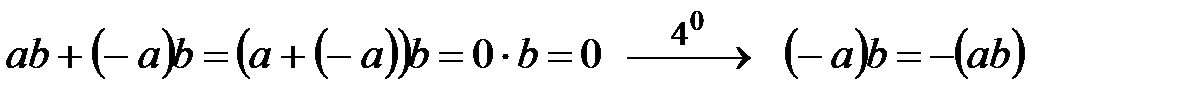. . 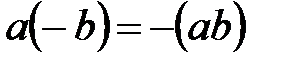Осымен бірдей дәлелденеді.

9⁰. .

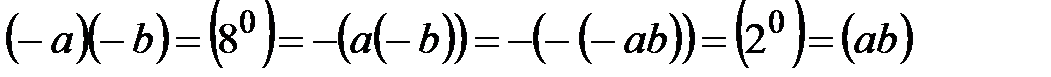10⁰. .

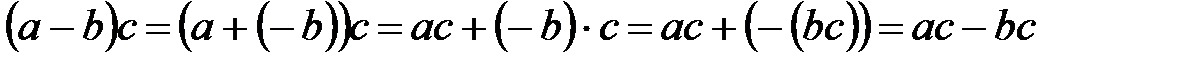Осымен бірдей 11⁰ дәлелденеді.

Ішкі сақина. 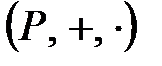сақина берілген болсын. 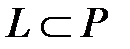. 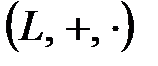алгебралық жүйесі сақина болатын болса, онда оны 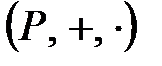сақинаның ішкі сақинасы деп атайды.

Мысалы, 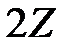- жұп сандар жиыны. 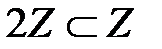. 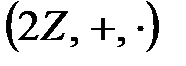сақина болады және ол 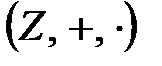сақинасының ішкі сақинасы болып табылады.

Ріс

Анықтама. Нөлден басқа барлық элементтерінің керісі болатын коммутативті сақинаны өріс деп атайды. Өрісті 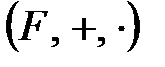деп белгілейміз. Олай болса өрісті сақинаның аксиомаларына қосса

8) ;

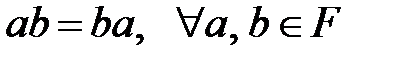9) .

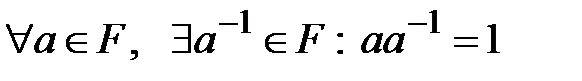Сонымен, 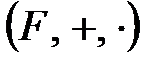алгебрасы өріс болса, онда 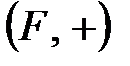және 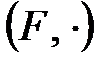екеуі де абельдік топ болады. Оларды сәйкес өрістің аддитивті және мультипликативті топтары деп атайды.

Мысал 2.2.2.

1) 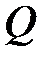рационал сандар жиыны қосу және көбейту амалдарына қатысты өріс құрайды. Өйткені, рационал сандардың қосындысы мен көбейтіндісі рационал сандар және рационал 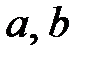сандары үшін 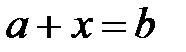теңдеуінің жалғыз шешімі бар (3⁰ қасиет), сол сияқты 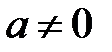болғанда 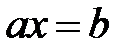теңдеуі үшін де дұрыс (7⁰ қасиет), ал 1⁰, 2⁰, 4⁰ - 6⁰ қасиеттері барлық нақты сандар үшін орындалады және дербес жағдайда рационал сандары үшін де орындалады. Сонымен, 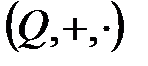және 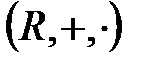өрістер болады.

2) 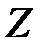бүтін сандар жиыны қосу және көбейту амалдарына қатысты өріс құрамайды. Өйткені, 7⁰ қасиет орындалмайды; мысалы, 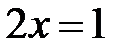теңдеуінің бүтін шешімдері болмайды. Бұл жиын сақинаға қатысты 1⁰ - 5⁰ қасиеттерден басқа 6⁰ қасиетті де қанағаттандырады, сондықтан ол коммутативті сақина болып табылады.

3) 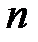-ші квадратты матрицалардың 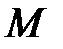жиыны қосу және көбейту амалдарына қатысты өріс құрамайды. Өйткені, матрицалардың көбейтіндісі коммутативті емес (6⁰ қасиет орындалмайды). Ол жиын үшін 1⁰ - 5⁰ қасиеттері орынды, сондықтан ол сақина болып табылады.