Нақты сандар өрісі
Алгебралық жүйесі, сызықтық реттелген жиын деп аталады, егер келесі шарттар орындалса:
1. 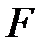 -гі кез-келген
-гі кез-келген 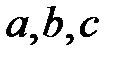 үшін, егер
үшін, егер 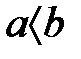 және
және 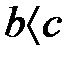 , онда
, онда 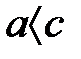 ;
;
2.  -гі кез-келген
-гі кез-келген  екі элементі үшін, берілген үш қатыстың біреуі орындалады:
екі элементі үшін, берілген үш қатыстың біреуі орындалады: 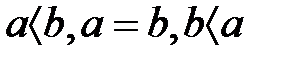 .
.
Анықтама: 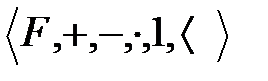 алгебралық жүйесі реттелген деп аталады, егер келесі шарттар орындалса:
алгебралық жүйесі реттелген деп аталады, егер келесі шарттар орындалса:
1. 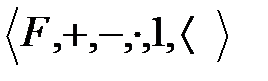 алгебрасы өріс болса;
алгебрасы өріс болса;
2. 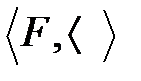 сызықтық реттелген жиын;
сызықтық реттелген жиын;
3. 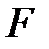 -гі кез-келген
-гі кез-келген 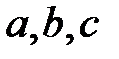 үшін, егер
үшін, егер 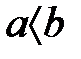 , онда
, онда 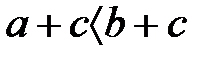 ;
;
4. 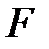 -гі кез-келген
-гі кез-келген 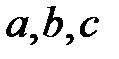 үшін, егер
үшін, егер 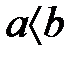 және
және 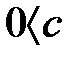 , онда
, онда 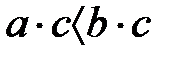
Реттелген өрістің 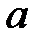 элементі оң болады, егер
элементі оң болады, егер  .
.
Анықтамабойынша 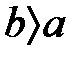 болады сонда ғана, егер
болады сонда ғана, егер  және
және  болады сонда, егер
болады сонда, егер  немесе
немесе 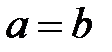 болса.
болса.
Мысалы:  рационал сандар өрісі болсын және <
рационал сандар өрісі болсын және < 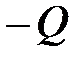 жиынындағы қатынас. 2.1 теоремасындағы 1-4 шарттары бойынша орындалады. Яғни
жиынындағы қатынас. 2.1 теоремасындағы 1-4 шарттары бойынша орындалады. Яғни 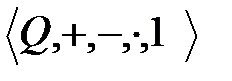 жүйесі реттелген өріс болады. Бұл жүйе реттелген рационал сандар өрісі деп аталады.
жүйесі реттелген өріс болады. Бұл жүйе реттелген рационал сандар өрісі деп аталады.
Теорема 4.1: Егер 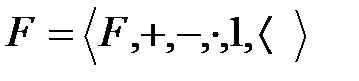 - реттелген өріс болсын және
- реттелген өріс болсын және 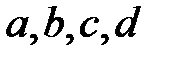 оның кез-келген элементтері. Онда:
оның кез-келген элементтері. Онда:
1. 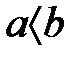 тек сол жағдайда, егер
тек сол жағдайда, егер 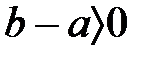
2.  -гі кез-келген
-гі кез-келген  элементі үшін, үш қатыстың бірі орындалады
элементі үшін, үш қатыстың бірі орындалады 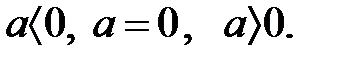
3. Егер 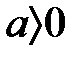 және
және 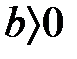 , онда
, онда 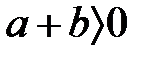 және
және 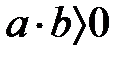 , яғни реттелген өрістің оң элементтерінің көбейтіндісі және қосындысы оң.
, яғни реттелген өрістің оң элементтерінің көбейтіндісі және қосындысы оң.
4. Егер 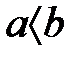 және
және 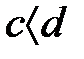 , онда
, онда 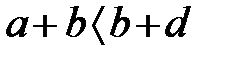
5. Егер  және
және  , онда
, онда 
6. Егер 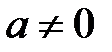 , онда
, онда 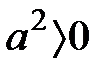
7. 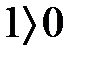 және
және 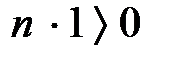 кез-келген
кез-келген 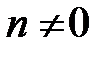
8. 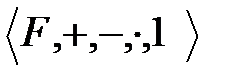 өрісі бүтін облыс.
өрісі бүтін облыс.
Дәлелдеу: (1) бірсарынды қосу бойынша 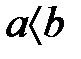 болады сонда ғана, егер
болады сонда ғана, егер 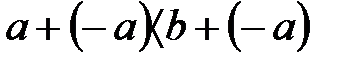 болса. Осыдан
болса. Осыдан 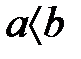 тек сонда, егер
тек сонда, егер 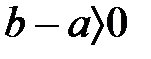 .
.
(2) тұжырым ақиқат, егер  - сызықтық реттелген жиын болса,
- сызықтық реттелген жиын болса,
(3) 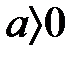 және
және 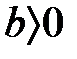 болғанда бірсарынды қосу бойынша шығады
болғанда бірсарынды қосу бойынша шығады 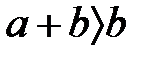 және
және 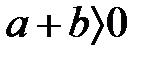 . Бірсарынды көбейту бойынша
. Бірсарынды көбейту бойынша 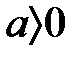 және
және 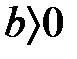 болғанда шығады
болғанда шығады 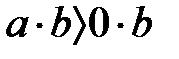 және
және 
(4) Егер 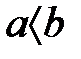 және
және 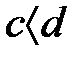 бірсарынды қосу бойынша
бірсарынды қосу бойынша 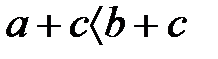 және
және 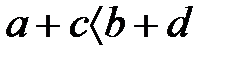 , осыдан
, осыдан 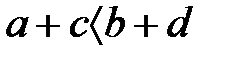
(5) (1)-ге қатысты 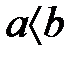 және
және 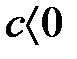 , онда
, онда 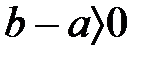 және
және 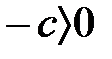 бірсарынды көбейту бойынша шығады
бірсарынды көбейту бойынша шығады 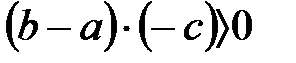 және
және  . Осыдан
. Осыдан 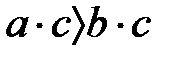
(6) Бірсарынды көбейту бойынша, егер 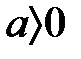 онда
онда 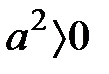 . Ал егер
. Ал егер 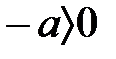 , онда
, онда 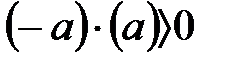 және
және 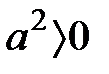
(7) 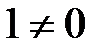 өрісінде (6) қатысты
өрісінде (6) қатысты  яғни реттелген өрістің оң элементтерінің жиынының қосындысы тұйық,
яғни реттелген өрістің оң элементтерінің жиынының қосындысы тұйық, 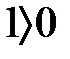 -ден шығады
-ден шығады  , яғни нөлден айрықша
, яғни нөлден айрықша  натурал сан үшін.
натурал сан үшін.
(8) Өрістің кез-келген 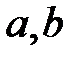 элементтері үшін, егер
элементтері үшін, егер  және
және 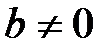 , онда
, онда 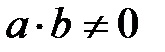 . Осыдан контрапозиция заңы бойынша, егер
. Осыдан контрапозиция заңы бойынша, егер 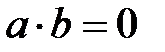 , онда
, онда 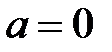 немесе
немесе 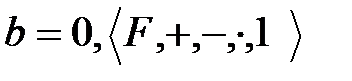 өрісі бүтін облыс болады.
өрісі бүтін облыс болады.
Анықтама: Реттелген өрістің  элементінің абсалют мәні
элементінің абсалют мәні 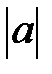 деп белгіленеді және келесі түрде анықталады:
деп белгіленеді және келесі түрде анықталады: 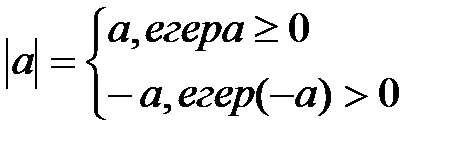
Анықтама: 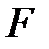 реттелген өрісі архимедовтік реттелген деп аталады, егер өрістің кез-келген
реттелген өрісі архимедовтік реттелген деп аталады, егер өрістің кез-келген 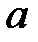 және
және 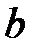 оң элементтері үшін,
оң элементтері үшін, 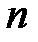 натурал саны болады,
натурал саны болады, 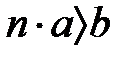 .
.
 -
- 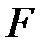 реттік өрістің элементтерінің шексіз бірізділігі болсын. Оны
реттік өрістің элементтерінің шексіз бірізділігі болсын. Оны 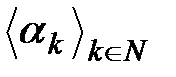 немесе
немесе 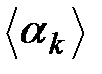 деп белгілейді.
деп белгілейді.
Анықтама:Нақты сандар жүйесі деп толық архимедовтік реттелген өрісті айтады.
Егер 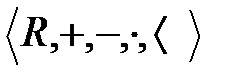 - нақты сандар жүйесі. Онда
- нақты сандар жүйесі. Онда 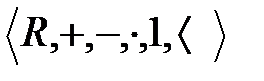 алгебрасы өріс, ол нақты сандар өрісі деп аталады.
алгебрасы өріс, ол нақты сандар өрісі деп аталады.  жиыны нақты сандар жиыны деп аталады.
жиыны нақты сандар жиыны деп аталады.
Теорема 4.2: 
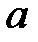 және
және  кез-келген нақты сандар үшін
кез-келген нақты сандар үшін  бүтін саны және
бүтін саны және 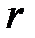 нақты саны болады
нақты саны болады

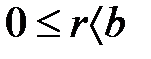
Дәлелдеу: 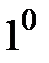 Егер
Егер  , онда
, онда 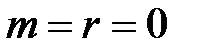 .
.  деп жориық, жиын
деп жориық, жиын  бос емес, себебі нақты сандар жүйесі архимедовтік реттелген. Натурал сандар жиыны реттелген және
бос емес, себебі нақты сандар жүйесі архимедовтік реттелген. Натурал сандар жиыны реттелген және 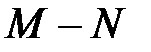 жиынының бос емес ішжиыны, сондықтан
жиынының бос емес ішжиыны, сондықтан 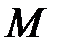 -нің ең кіші шамасы бар. Егер
-нің ең кіші шамасы бар. Егер 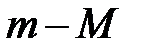 жиынының ең кіші шамасы, онда
жиынының ең кіші шамасы, онда
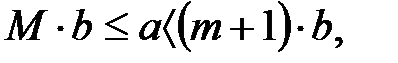
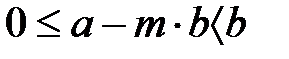 .
.
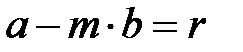 десек,
десек, 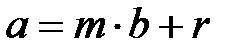 ,
, 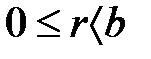 деп аламыз.
деп аламыз.
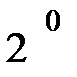
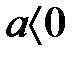 деп жорысақ, онда
деп жорысақ, онда 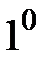 дәлелденгендей
дәлелденгендей  және
және 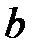 оң сандары үшін
оң сандары үшін 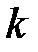 натурал саны және
натурал саны және 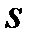 нақты саны бар
нақты саны бар
 ,
, 
Осыдан 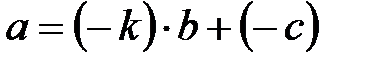 . Егер
. Егер 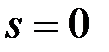 болса, іздегенімізді табамыз, ал егер
болса, іздегенімізді табамыз, ал егер 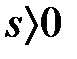 , онда
, онда 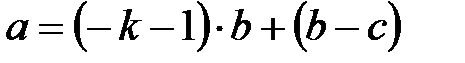
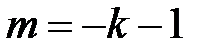
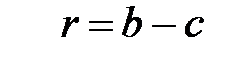 жориық, онда
жориық, онда  ,
, 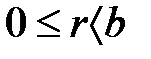 .
.  – нөлден өзгеше натурал сан. Оң нақты санның
– нөлден өзгеше натурал сан. Оң нақты санның 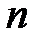 - дәрежелі арифметикалық түбірін енгіземіз. Келесі теореманы дәлелдейік.
- дәрежелі арифметикалық түбірін енгіземіз. Келесі теореманы дәлелдейік.
Теорема 4.3: Кез-келген оң 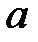 саны үшін бір ғана оң нақты сан
саны үшін бір ғана оң нақты сан 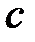 болады, онда
болады, онда  .
.
Дәлелдеу:  функциясы
функциясы 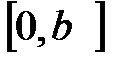 тұйық интервалында анықталған болсын, мұндағы
тұйық интервалында анықталған болсын, мұндағы 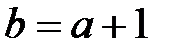 .
.  функциясы берілген интервалда үздіксіз,
функциясы берілген интервалда үздіксіз, 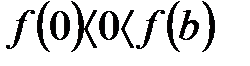 болғандықтан әр түрлі таңбаларды қабылдайды.
болғандықтан әр түрлі таңбаларды қабылдайды.
Теорема бойынша 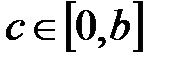 , ол үшін
, ол үшін 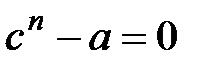 , яғни (1)
, яғни (1) 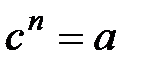 .
.
Шынында, 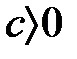 .
. 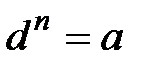 деп оң
деп оң 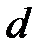 санына жориық, мұнда
санына жориық, мұнда 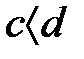 , онда
, онда 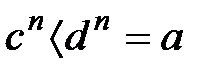 , бірақ ол (1) қайшы келеді. Ал егер
, бірақ ол (1) қайшы келеді. Ал егер  , онда
, онда 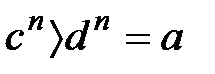 , бірақ та бұл да (1) қарама қарсы. Осыдан
, бірақ та бұл да (1) қарама қарсы. Осыдан  .
.
Анықтама:  – оң нақты сан және
– оң нақты сан және 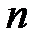 – нөлден өзгеше натурал сан. Бір ғана
– нөлден өзгеше натурал сан. Бір ғана 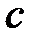 - оң нақты саны, егер
- оң нақты саны, егер 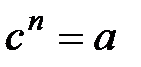 арифметикалық немесе
арифметикалық немесе 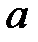 -дан
-дан 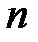 -дәрежелі басты түбір деп аталады және
-дәрежелі басты түбір деп аталады және  немесе
немесе  деп белгіленеді.
деп белгіленеді.
Дата добавления: 2016-04-02; просмотров: 2975;
