Сақина және өріс

Сақинаның қарапайым қасиеттері

Өріс

Өрістің қарапайым қасиеттері

Рационал сандар өрісі

Комплекс сандар өрісі

Нақты сандар өрісі

Өрістің алгебралық жай кеңейтілуі

Бөлшектің бөліміндегі алгебралық иррационалдықтан құтылу

Өрістің күрделі алгебралық кеңейтілуі

Топта бір алгебралық амал анықталған болса, сақинада екі алгебралық амал анықталады. Оның біріншісі аддитивті түрде «+» болады да, екіншісі мультипликативті түрде немесе оған ұқсас болады.

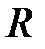нақты сандар жиыны қосу амалына қатысты топ құрайды және ол коммутативтік топ болып табылады (мысал 2.1.7). Басқаша айтқанда, нақты сандардағы қосу амалы келесі шарттарды қанағаттандырады ( 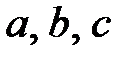- 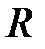жиынының кез келген элементтері):

1⁰. 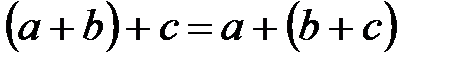(қосудың ассоциативтілігі);

2⁰. 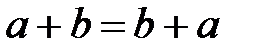(қосудың коммутативтілігі);

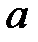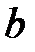3⁰. Кез келген және сандары үшін 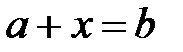теңдеуінің бір ғана шешімі болады (қосудың қайтымдылығы);

Сонымен қатар, қосу амалы басқадай көбейту амалымен байланысқан (дистрибутивтік (үлестірімділік) заңдылығымен):

4⁰. 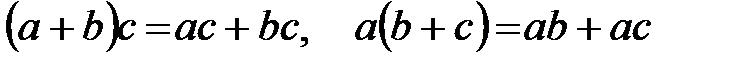(көбейтудің қосуға қатысты оң жақ және сол жақ дистрибутивтілігі);

Көбейту амалы 1⁰-3⁰ шарттарды қанағаттандырады:

5⁰. 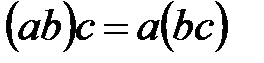(көбейтудің ассоциативтілігі);

6⁰. 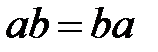(көбейтудің коммутативтілігі);

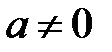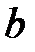7⁰. Кез келген және сандары үшін 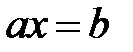теңдеуінің бір ғана шешімі болады (көбейтудің шектелген қайтымдылығы).

Анықтама. Егер 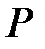жиынының кез келген 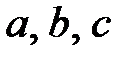элементтері үшін жоғарыдағы 1⁰ – 5⁰ қасиеттері орындалатын болса, онда қосу және көбейту амалдары анықталған 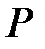жиыны сақина деп аталады және егер 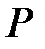жиынында 0 -ден өзгеше элементтер болып, жоғарыдағы 1⁰ – 7⁰ қасиеттері орындалатын болса, онда 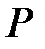жиыны өріс деп аталады.

Анықтамадан, өріс құрайтын жиындар сақина болып табылады. Өріс құрамайтын сақиналар кездеседі, яғни 6⁰ – 7⁰ қасиеттері орындалмайды.

Сонымен, 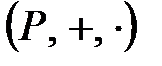алгебралық жүйесі төмендегі аксиомаларды қанағаттандырса, онда оны сақина деп атайды:

С1) ;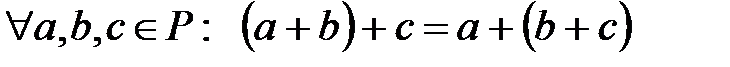

С2) ;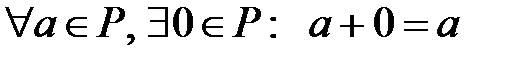

С3) ;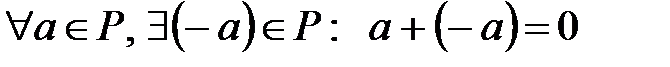

С4) ;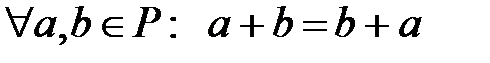

С5) ;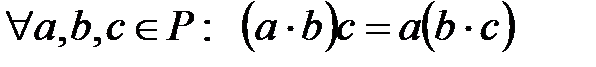

С6) , ;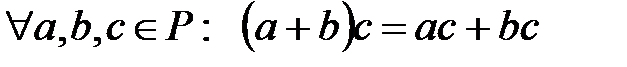

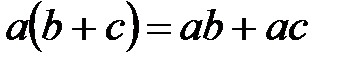С7) .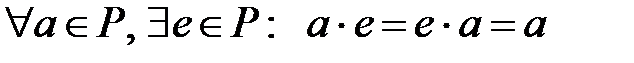

Бұл аксиомалардан 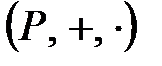сақина болса, 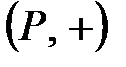абельдік топ болатыны шығады. 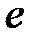элементті сақинаның бірлігі деп атайды, көбінесе оны 1 деп белгілейді.

Егер сақинада 6⁰ қасиет немесе С8) 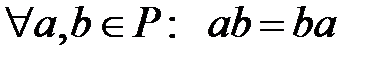аксиома орындалса, онда 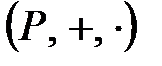сақинасын коммутативті сақина деп атайды.

Мысал 2.2.1.

1) 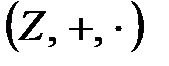бүтін сандар сақинасы;

2) 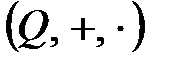рационал сандар сақинасы;

3) 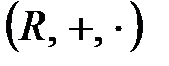нақты сандар сақинасы;

4) 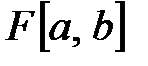- мен 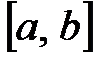кесіндіде анықталған барлық үзіліссіз функциялардың жиыны:

а) 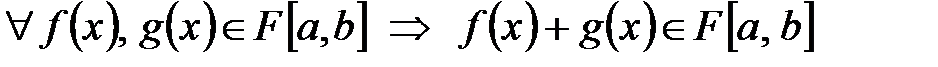функцияларды қосу;

б) 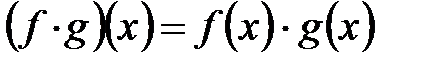функцияларды көбейту. 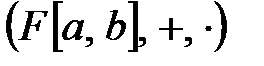сақина болады.