Крутящий момент от центробежных сил.
Рассмотрим элемент лопатки, расположенный в окрестности точки А. Площадь этого элемента – dF, высота – dz.
| x |
| φ |
| dC |
| dz |
| u |
| y |
| x |
| x |
| y |
| т.А |
| т.А |
| dF |
| dCх |
| x |
| -y |
| Рис. 19. К определению крутящего момента от центробежных сил |
Центробежная сила, действующая на этот элемент, составит
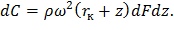
Эта сила направлена по радиусу, проходящему через центр масс элемента, то есть через точку А. Крутящий момент будет создаваться проекцией силы dC на ось x, то есть
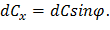
В силу малости угла ϕ можно считать, что
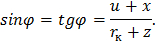
Тогда крутящий момент от центробежных сил, действующий на элемент dFdz составит
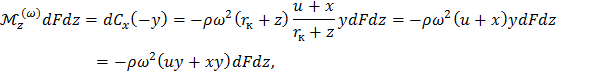
где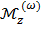 
– крутящий момент от центробежных сил, приходящийся на единицу объема. Так как смещение u много меньше линейных размера профиля (x и y), то первым слагаемым, стоящим в скобках, можно пренебречь:
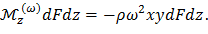
Тогда крутящий момент от центробежных сил, действующий на элемент dz, то есть элемент образованный двумя сечениями лопатки перпендикулярными оси z и отстоящими друг от друга на расстояние dz, составит
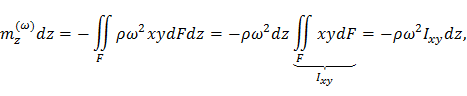
где mz(ω) – момент от центробежных сил, приходящийся на единицу длины лопатки.
Крутящий момент от центробежных сил в любом сечение лопатки с координатой z составит
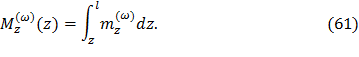
Дата добавления: 2016-02-16; просмотров: 839;