Расчет нестационарных температурных напряжений в лопатках.

Разложим полную осевую деформацию ε в ряд Тейлора в окрестности центра масс сечения (ξ=0, η=0) и ограничимся линейными членами разложения:

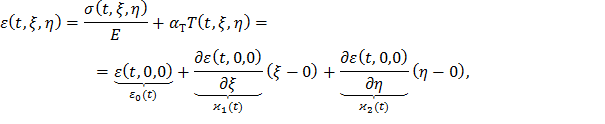
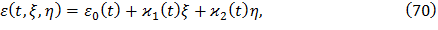
где σ(t,ξ,η) – упругие нормальные напряжения по оси z; T(t,ξ,η) – температура материала лопатки в любой точке профиля; ε(t,ξ,η) – полная деформация по оси z; 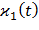– кривизна термоупругой оси лопатки в главной плоскости ξOz; 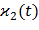– кривизна той же оси в главной плоскости ηOz; ξ, η – координаты произвольной точки поперечного сечения в главных осях.

Напряжения выразим из формул (70) так

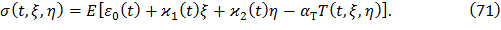
Величины ε₀, 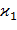, 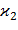– подлежат определению.

В упругих условиях температурные напряжения можно рассматривать независимо от силовых. Поэтому при расчете чисто температурных напряжений все внешние силы, действующие на лопатку, принимаются равными нулю.

Рассмотрим лопатку без связей.

1. Растягивающая сила

Подставим формулу (71) в уравнение равновесия (72):

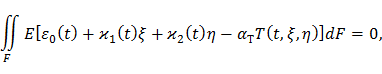
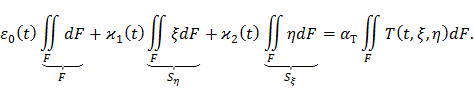
Статические моменты S_η и S_ξ относительно главных центральных осей инерции равны нулю, поэтому

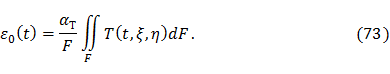
Обозначим

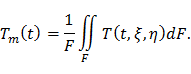
тогда

где T_m – средняя по сечению температура материала лопатки.

2. Изгибающий момент относительно оси η

Подставим формулу (71) в уравнение равновесия (75):

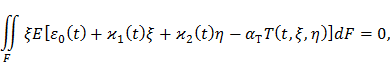
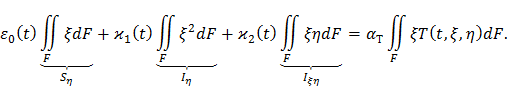
Моменты S_η и I_ξη относительно главных центральных осей инерции равны нулю, поэтому

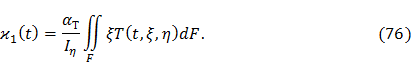
3. Изгибающий момент относительно оси ξ

Подставим формулу (71) в уравнение равновесия (77):

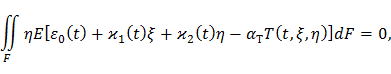
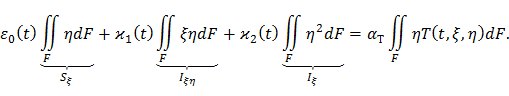
Моменты S_ξ и I_ξη относительно главных центральных осей инерции равны нулю, поэтому

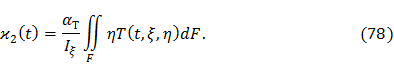
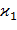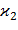Получаемые по формулам (74), (76) и (78) величины ε₀, и являются функциями времени.

При использование приближенного решения (69) вместо кратных интегралов требуется вычислить одномерные интегралы, если dF=δ(s)ds и s=0…s₀.

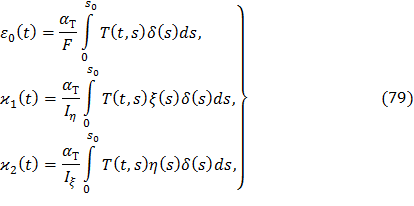
где ξ(s) и η(s) – координаты скелетной линии; δ(s) – толщина профиля по нормали к скелетной линии.

После определения величин ε₀, 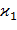и 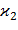по формулам (74), (76) и (78) или по (79) находят поле температурных напряжений по (71).