Безмоментная рабочая лопатка

Уравнения (51) позволяют определить форму оси безмоментной лопатки. Безмоментной называется лопатка, у которой суммарный изгибающий момент в каждом сечение равен нулю. Для такой лопатки смещения в нагруженном и не нагруженном состояниях совпадают, то есть u=u₀, υ=υ₀. Тогда согласно (51) имеем

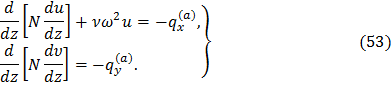
Рассмотрим активную лопатку постоянного профиля. В этом случае q_x^(a)=const, а q_y^(a)=0. Рассмотрим второе уравнение системы (53)

Так как растягивающая сила есть величина, нелинейно меняющаяся по длине лопатки N(z), то уравнение (54) будет удовлетворяться только в том случае, если

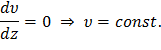
Согласно граничным условиям υ(0)=0, имеем υ=0.

Рассмотрим первое уравнение системы (53)

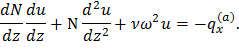
Решение этого уравнения будем искать в виде u(z)=az. Тогда

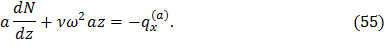
Согласно уравнению равновесия (5)

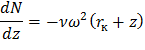
выражение (55) примет вид

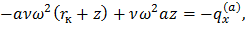
Тогда

Таким образом, для полной компенсации аэродинамического изгиба центробежными силами лопатку следует устанавливать наклонно к оси z со смещением или выносом вершины в сторону вращения на величину

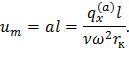
Установка лопатки с выносом дает возможность компенсировать лишь постоянную составляющую аэродинамической нагрузки.