Лопатка с показательным законом изменения площади сечения по высоте.

В этом случае

Распределение растягивающих напряжений по высоте лопатки определяется следующей зависимостью:

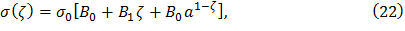
где σ₀ – напряжение в корне лопатки постоянного сечения при тех же величинах l и υ, что и для лопатки переменного сечения;

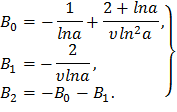
В отличие от лопаток с постоянным и линейным законами распределения сечений по высоте, в рассматриваемом случае максимальное растягивающее напряжение может достигаться в сечении выше корневого. Для определения его координаты исследуем функцию (22) на максимум, вычислив ее производную и приравняв к нулю.

Тогда

Прологарифмируем обе части последнего уравнения:

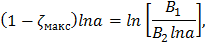
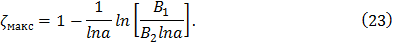
Если по формуле (23) получаются отрицательные значения ζ_макс, то наибольшее растягивающее напряжение достигается в корневом сечение (ζ_макс=0). Сама величина максимального растягивающего напряжения вычисляется с использованием функции (22):

Для количественного сравнения эффективности различных законов снижения растягивающих напряжений в корневой области рабочей лопатки используется коэффициент разгрузки

где σ_макс – наибольшее напряжение в лопатке переменного сечения; σ₀ – напряжение в корне лопатки постоянного сечения при тех же величинах l и υ, что и для лопатки переменного сечения. Лопатки с показательным законом изменения площадей имеют большую разгрузку (меньшие значение k) при равных a и υ по сравнению с рабочими лопатками с линейным законом изменения площадей.