Лопатка с постоянной площадью поперечного сечения.

В этом случае F(z)=F=const. Тогда выражение для растягивающего усилия примет следующий вид:

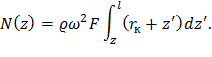
Вычислим интеграл в полученной формуле:

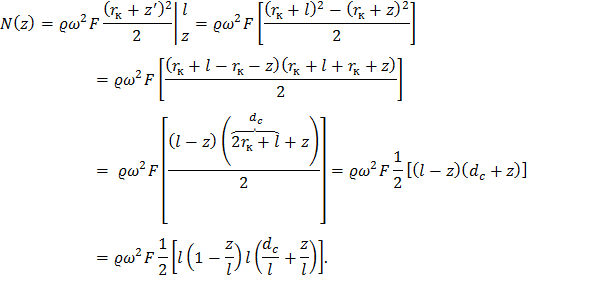
Обозначим

где ζ – относительная координата по высоте лопатки; υ – веерность лопатки; d_c – средний диаметр ступени.

С учетом введенных обозначений имеем

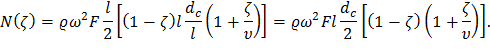
Окончательно получим

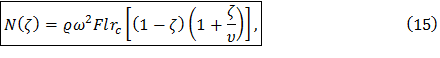
где r_с – средний радиус ступени.

Распределение растягивающих напряжений по высоте лопатки с постоянной площадью поперечного сечения согласно формулам (10) и (15) запишется следующим образом:

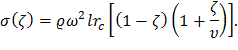
Обозначив

окончательно получим

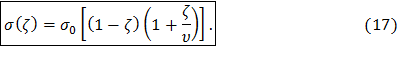
Выясним физический смысл величины σ₀. Для этого исследуем функцию σ(ζ) на экстремум, вычислив ее производную и приравняв к нулю:

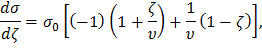
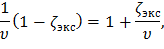
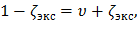
Из физического смысла очевидно, что экстремальное значение ζ_экс будет соответствовать величине, доставляющей функции σ(ζ) максимум, то есть ζ_экс = ζ_макс. Веерность даже самых длинных лопаток последних ступеней турбины имеет порядок 2 – 3, следовательно, согласно формуле (18), ζ_макс принимает отрицательные величины. С физической точки зрения это означает, что растягивающие напряжения в лопатке постоянного сечения достигают максимального значения в корне. Так, применяя формулу (17) при ζ_макс =0 имеем,

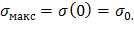
Таким образом, σ₀ – растягивающее напряжение в корневом сечении лопатки с постоянной по высоте площадью поперечного сечения.

Для снижения растягивающих напряжений в корневом сечении лопатки с веерностью меньше 10 выполняют переменного сечения с уменьшающейся от корня к периферии площадью.