Лопатка равной прочности.

Лопатка равной прочности имеет два участка. На первом участке, от корневого сечения до сечения с координатой z=z^*, закон изменения площадей выбирают так, чтобы растягивающее напряжение было постоянно по длине этого участка. На втором участке z^*≤z≤l лопатка имеет постоянное поперечное сечение.

Рассмотрим первый участок. Здесь растягивающие напряжения постоянны

где σ₁ – постоянное напряжение на первом участке. С учетом формулы (13) последнее выражение примет вид:

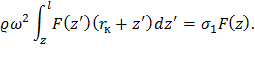
Продифференцировав, полученное соотношение преобразуем в обычное дифференциальное уравнение:

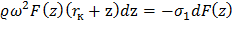
или после разделения переменных

Знак «минус» в приведенных уравнениях означает, что площадь поперечного сечения должна уменьшаться от корня к периферии, то есть при dz>0 → dF<0.

Проинтегрируем уравнение (24) в диапазоне от корня до рассматриваемого сечения с координатой z:

Таким образом, закон изменения площади поперечного сечения по высоте лопатки равной прочности окончательно представится в виде

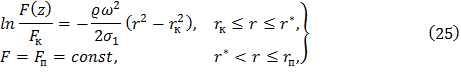
где r=r_к+z – текущий радиус.

Определим координату z^* сечения, разделяющего первый и второй участки лопатки равной прочности. На первом участке напряжения остаются постоянными и являются наибольшими для рассматриваемой лопатки, то есть σ₁=σ_макс. Начиная с сечения с координатой z^* (второй участок), они начинают снижаться и достигают нуля на периферии. Таким образом, растягивающее напряжение в сечении z^* составит σ_макс. Площадь поперечного сечения на первом участке меняется согласно первому уравнению (25), на втором – остается постоянным и равным периферийному. Следовательно, в сечении с координатой z^* оно также будет равно периферийному.

На границе участков при z=z^* растягивающее напряжение и площадь поперечного сечения должны одновременно удовлетворять уравнениям (17) и (25):

где

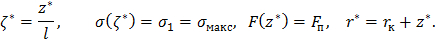
Тогда

Согласно введенным ранее обозначениям имеем

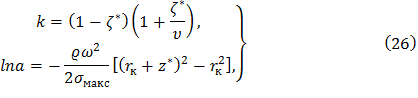
где k – коэффициент разгрузки; а – отношение периферийной и корневой площадей поперечных сечений лопатки.

Рассмотрим второе уравнение из (26). Преобразуем комплекс в квадратных скобках:

В полученном выражении вынесем величину l за скобку

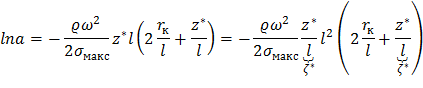
и с учетом ранее введенных обозначений получим

Рассмотрим комплекс

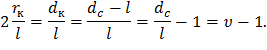
Тогда выражение (27) примет следующий вид:

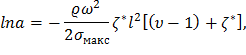
где d_к и d_с – соответственно корневой и средний диаметры колеса.

Перегруппировав множители в полученном выражении

получим

Рассмотрим первое уравнение системы (26). Раскрыв скобки, получим

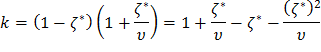
или

С учетом выражений (28) и (29), система (26) примет следующий вид:

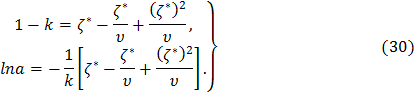
Сравнивая первое и второе уравнения системы (30), легко установить взаимосвязь между параметрами k и a:

а координату ζ^* получим из решения первого уравнения:

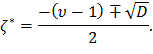
Минимальные величины веерности, соответствующие длинным лопаткам последних ступеней турбины, составляют υ=2…3, а (υ-1) – всегда больше нуля. Поэтому из двух возможных решений уравнения (32) физический смысл имеет только

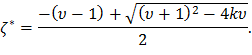
После элементарных преобразований окончательно получим

Лопатка равной прочности имеет наибольшую разгрузку из всех сравниваемых законов.