Интерференция света в тонких пленках. Линии равного наклона и равной толщины. Просветление оптики
Интерференция в пленках и пластинках
При освещении тонкой пленки происходит наложение от одного и того же источника, отразившихся от передней и задней поверхностей пленки. При этом может возникнуть интерференция. Если свет белый, то интерференционные полосы окрашены. Поэтому явление получило название цветов тонких пленок.
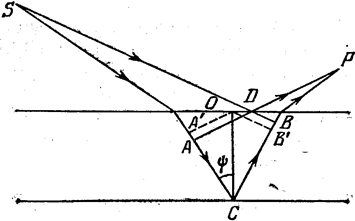 |
Рис.1а
Оно легко наблюдается на стенках мыльных пузырей, на тонких
пленках масла или нефти, плавающих на поверхности воды
2. Рассмотрим сначала плоскопараллельную пластинку толщины d с показателем преломления n, освещаемую точечным источником света S (рис.1а). При отражении от поверхностей плёнки возникает оптическая разность хода между соответствующими отраженными волнами. Вычислим ее в какой-либо произвольно выбранной точке Р.
Если пластинка тонкая, то для вычисляемой оптической разности хода можно написать: D == (SAXBP) — (SDP). Через точку О, симметрично расположенную на верхней поверхности пластинки между точками A и B, проведем плоскости ОA' и ОB¢ (начерченные пунктиром), параллельные плоскостям DA и DB. Тогда D== (A'СВ') = 2 (A'С) = 2nd cos y, где y— угол преломления.
Волны, отраженные от передней и задней поверхностей пластинки, должны при интерференции гасить друг друга. Их фазы должны быть противоположны, т.е. оптическая разность хода D при d®0 должна стремиться к l/2. Поэтому к прежнему выражению для D надо прибавить или отнять l/2 (что совершенно безразлично). После этого получим
D=2dncosy+l/2.
Все рассуждения и результаты остаются в силе и для случая, когда точка Р лежит по другую сторону пластинки. В этом случае отраженные лучи расходящиеся, в точке Р пересекаются не сами лучи, а их продолжения за пластинку. Для наблюдения интерференции в точке Р надо отраженные лучи сделать сходящимися с помощью собирающей линзы или вогнутого зеркала. Тогда интерференцию следует наблюдать в точке P¢, оптически сопряженной с точкой Р.
Формула (1) справедлива и для тонких пластинок переменной толщины. Только в этом случае под d надо понимать толщину пластинки в том ее месте, где происходит отражение лучей, пересекающихся в точке Р. Но в точку Р от точечного источника света могут попадать, вообще говоря, только два луча. Отсюда cледует, что в случае точечного монохроматического источника света каждая точка пространства характеризуется вполне определенной разностью хода приходящих в нее отраженных лучей. Поэтому устойчивая интерференция должна наблюдаться в каждой точке пространства.
Интерференция в тонких пленках рассматривалась выше как двухлучевая интерференция. Мы ограничились интерференцией только двух волн, одна из которых получилась при однократном отражении от верхней, а другая — от нижней поверхностей пленки, Многократными отражениями мы пренебрегли. Это можно делать, когда коэффициент отражения невелик.
Допустим теперь, что пластинка толстая и строго плоскопараллельная. Пусть она освещается параллельным пучком света. Формально это соответствует случаю точечного бесконечно удаленного источника S. Отраженные лучи будут также параллельными, т. е. точка наблюдения Р удалится в бесконечность. При постоянной толщине пластинки d оптическая разность хода между отраженными лучами 2dn cos y +l/2 зависит только от угла наклона падающих лучей. Угол y может принимать всевозможные значения, если источник света протяженный и имеет конечные угловые размеры.
| <== предыдущая лекция | | | следующая лекция ==> |
| Пространственная когерентность. | | | Интерферометр Майкельсона |
Дата добавления: 2016-04-19; просмотров: 2334;
