Результаты экспериментальных измерений

4.4.3 Графоаналитическим методом засечек для всех 3 состояний цепи построить векторные диаграммы напряжения и токов.

4.4.4 По данным таблицы 4.2 и известной величине напряжения на входе цепи U произвести поверочный расчет токораспределения в цепи методом комплексных чисел.

4.4.4 По данным таблицы 4.2 и известной величине напряжения на входе цепи U произвести проверочный расчет токораспределения в цепи методом проводимостей.

Сравнить результаты трех методов расчета. Сделать выводы по работе и ответить на контрольные вопросы.

4.5 Сводка основных формул (методики расчета)

В разветвленной цепи синусоидального тока (рис. 4.2) все параллельно соединенные приемники находятся под одинаковым напряжением, а в каждой параллельной ветви устанавливается синусоидальный ток.

u_i = U_m sin (wt), i_i = I_mi sin (wt ± j_i),

где u_i, i_i, U_m, I_mi – соответственно мгновенные и амплитудные значения напряжения и тока; w= 2pf – угловая частота; t – время, f – частота синусоидального тока; j_i = arctg(Х_i/R_i) – угол сдвига фаз между напряжением и током i-й ветви; R_i, Х_i – соответственно активное и реактивное сопротивления данной ветви.

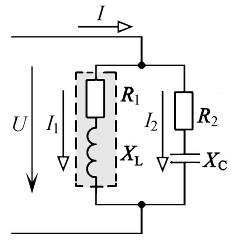
Рис. 4.2. Разветвленная цепь синусоидального тока (пример)

Ток I в неразветвленной цепи можно найти либо из векторных диаграмм как геометрическую сумму токов отдельных приемников, т.е.

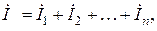
либо аналитически

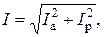
где I_a и I_p – соответственно активная и реактивная составляющие общего тока,

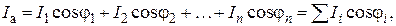
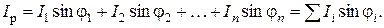
Величину угла сдвига фаз j между напряжением U и током I₁ в неразветвленной части цепи можно определить по формуле

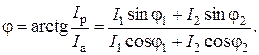
При значении угла j ≠ 0 в цепи преобладает индуктивная либо емкостная нагрузка и ток I отстает, либо опережает по фазе напряжение U. Если угол j= 0, то ток I и напряжение U совпадают по фазе, такое состояние электрической цепи называют резонансом токов.

Резонанс токов возникает при равенстве реактивных проводимостей ветвей (b_L = b_C) одна из которых содержит индуктивную катушку, а другая конденсатор и характеризуется следующими параметрами.

Ток в неразветвленной части цепи принимает минимальное значение

,

где g₁ и g₂ – активные проводимости параллельных ветвей.

В цепи происходит взаимный обмен энергией магнитного поля индуктивной катушки и электрического поля конденсатора. Коэффициент мощности цепи cosj = 1 и цепь потребляет только активную мощность, т.е.

S = P = U∙I.

Реактивные токи в ветвях цепи I_p1 и I_p2, сдвинутые относительно друг друга по фазе на 180^о, равны между собой и всегда компенсируют друг друга. Их абсолютные величины могут превышать ток в неразветвленной части цепи

При резонансе токов реактивные проводимости b_L и b_C и реактивные мощности тока Q_L и Q_C также равны между собой

.

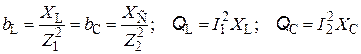Резонанс токов характеризуется резонансной частотой

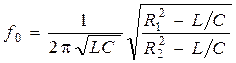
и может быть достигнут путем изменения, как частоты синусоидального напряжения, так и параметров R₁, R₂, L, C параллельных ветвей цепи.

Резонанс токов используют в установках для повышения коэффициента мощности тока потребителя, подключая параллельно индуктивному приемнику конденсаторную батарею емкостью

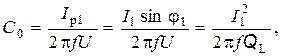
которая обеспечивает коэффициент мощности cosj= 1.

Обычно коэффициент мощности установок доводят только до значения cosj ≈ 0,92 – 0,95, т.к. дальнейшее его повышение вызывает значительное увеличение емкости конденсаторной батареи. Емкость С конденсаторной батареи определяют в этом случае по формуле

[мкФ],

где j₁ и j₂ – углы сдвига фаз между напряжением U и током I соответственно до компенсации и при ней.

Расчет разветвленной цепи переменного тока может быть осуществлен графоаналитическим методом, символическим методом (метод комплексных чисел) и методом проводимости.

4.5.1 Расчет цепи (рис. 4.1) графоаналитическим методом

Активное сопротивление резистора R и индуктивной катушки R_К.

.

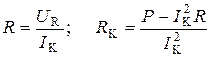Полное и реактивное сопротивления индуктивной катушки

.

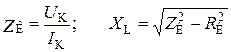Индуктивность катушки

.

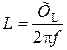Реактивное сопротивление конденсатора и его емкость

мкФ.

Полная и реактивная мощности цепи

.

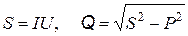Коэффициент мощности

.

Активные I_a и реактивные I_p составляющие токов цепи и ветвей:

I_a = I ∙cos j, Ip = I ∙sin j,

I_a1 = I_K ∙ cos j_K, I_p1 = I_k ∙ sin j_K,

I_a2 = 0, I_p2 = I_C = U/X_C.

Построение векторных диаграмм для цепей с параллельным соединением начинают с вектора напряжения U, относительно которого в выбранном масштабе циркулем методом засечек строят векторы токов I_K и I_С

.

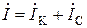На рисунке 4.3 представлены векторные диаграммы цепи, когда

j >0, j < 0 и j = 0.

Рис 4.3. Варианты векторных диаграмм параллельной цепи

4.5.2. Расчет цепи (рис. 4.1) символическим методом

Все методы расчета линейных цепей постоянного тока могут быть применены для расчета сложных цепей синусоидального тока, если пользоваться символическим методом.

Вектор приложенного к цепи напряжения условно направляют по вещественной оси, т.е.

.

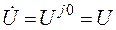Выражают полные сопротивления ветвей цепи в комплексной форме

; .

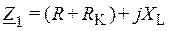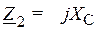Определяют полный комплексный ток, активную и реактивную составляющие и модуль этого тока первой ветви

,

.

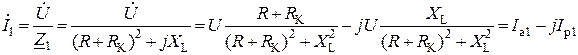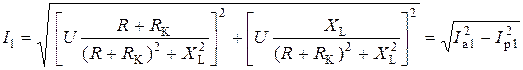Определяют полный комплексный ток, реактивную составляющую и модуль этого тока второй ветви

, .

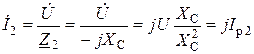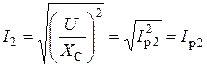Сложение полных комплексных токов 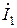и 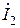по первому закону Кирхгофа позволяет определить полный комплексный ток в неразветвленной части цепи 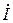, т.е.

,

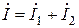или по закону Ома .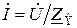

Для параллельного соединения двух ветвей эквивалентное комплексное сопротивление рассчитывается по формуле

.

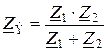Модуль тока I находят после определения его вещественной и мнимой частей (соответственно активной и реактивной составляющих) аналогично, как и токи I₁ и I₂. По полученным значениям на комплексной плоскости методом засечек строят диаграмму токов.

Полную комплексную мощность тока цепи и комплексные мощности токов ветвей через активные и реактивные составляющие определяют по формулам:

;

;

,

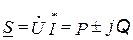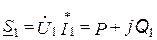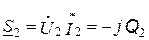где 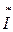– сопряженный полный комплексный ток в неразветвленной части цепи; P, Q – соответственно вещественная и мнимая составляющие полной комплексной мощности цепи.

Полную мощность тока цепи (модуль полной комплексной мощности) и мощности токов ветвей определяют по формулам:

; ; .

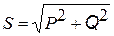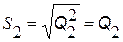4.5.3 Расчет цепи методом проводимостей

Данный метод рекомендуется использовать при числе параллельных ветвей в цепи более двух.

Для исследуемой цепи (рис. 4.1)определяют активные (g), реактивные (b) и полные (у) проводимости каждой ветви (См)

; ; ;

.

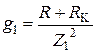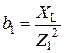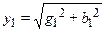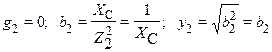Определяют активную, реактивную и полную проводимости всего соединении (две ветви)

;

.

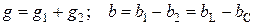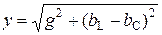По найденным значениям проводимостей разветвления можно определить сопротивления эквивалентной последовательности цепи (Ом)

.

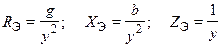Ток в неразветвленной части цепи, и токи в ветвях находят по формулам:

.

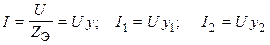Активные I_a и реактивные I_p составляющие тока до разветвления и токов в ветвях определяют из соответствующих проводимостей

;

.

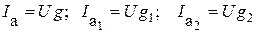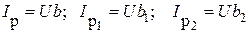Трехфазная цепь с ПРИЕМНИКАМИ,