Результаты аналитических расчетов
(косвенные измерения)
| Последовательная цепь | R, Ом | ZК, Ом | RК, Ом | XL, Ом | Xc, Ом | L, Гн | С, мкФ | S, BA | Q, вар | сosφ | φ, гр |
| RC | |||||||||||
| RL | |||||||||||
| RLC | |||||||||||
| RLC (резонанс) |
3.4.4 Произвести измерения тока, активной мощности, напряжения источника питания и падений напряжений на элементах последовательной RLC-цепи (опыт № 3).
Данный этап исследования выполняется в следующей последовательности:
1) собрать электрическую цепь с последовательным (неразветвленным) соединением резистора R, конденсатора C и индуктивной катушки L (рис. 3.3) со значениями параметров, которые задаются преподавателем;
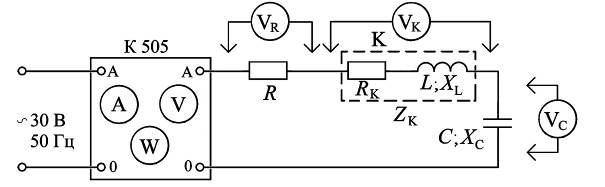
Рис. 3.3. Принципиальная электрическая схема исследования
последовательной RLС-цепи
2) после проверки руководителем правильности соединений подключить источник питания;
3) произвести измерение напряжения U, тока I, активной мощности тока P источника питания и падений напряжений на резисторе UR, конденсаторе UC и на индуктивной катушке UK. Результаты измерений записать в таблицу 3.1.
4) по данным таблицы 3.1 для RLС-цепи рассчитать величины полного ZK, активного RK , реактивного XL сопротивления и индуктивности катушки L, реактивного XС сопротивления и емкости конденсатора С, а затем вычислить величины полной S и реактивной Q мощностей, коэффициента мощности тока λ = cosφ и значение угла сдвига фаз φмежду током и напряжением. Результаты расчетов записать в таблицу 3.2.
3.4.5 Исследовать условия возникновения в последовательной RLC-цепи явление резонанса напряжений (опыт № 4).
Данный этап выполняется в следующей последовательности:
1) в электрической цепи (рис. 3.3) путем перебора тумблерами магазина конденсаторов стенда «Уралочка» подобрать такое значение параллельного соединения конденсаторов (на схеме это емкость C), при котором ток I в цепи принимает максимальное значение;
2) произвести измерение значений напряжения U, тока I, активной мощности тока P источника питания и падений напряжений на резисторе UR, конденсаторе UC и на индуктивной катушке UK, которые записать в таблицу 3.1;
3) по данным таблицы 3.1 рассчитать величины активного RK , реактивного XL сопротивления и индуктивность катушки L, реактивного XС сопротивления и емкости конденсатора С, полного сопротивления Z, а затем вычислить величины полной S и реактивной Q мощностей, коэффициента мощности тока λ = cosφ и значение угла сдвига фаз φмежду током и напряжением. Результаты расчетов записать в таблицу 3.2;
3.4.6 Построить для всех опытов в масштабе, используя линейку, циркуль и транспортир, векторные диаграммы напряжений и тока.
3.5. Сводка основных формул (методики расчета).
Неразветвленная электрическая цепь синусоидального тока с последовательно соединенными приемниками, характеризуемыми сосредоточенными параметрами R (активное сопротивление), L (индуктивность) и C (ёмкость), которые не зависят от тока и напряжения на зажимах соответствующих элементов, называется линейной RLC-цепью (рис. 3.4).
При подключении такой цепи к источнику синусоидального напряжения
u = Um sinωt
в ней возникает синусоидальный ток
i = Im sin(ω t ± φ),
где u, Um – соответственно мгновенное напряжение и амплитуда напряжения; i, Im – соответственно мгновенный ток и амплитуда тока; ω = 2πf – угловая частота; φ – угол сдвига фаз между током и напряжением; f – частота колебаний синусоидального тока.
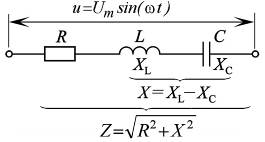
Рис. 3.4. Схема неразветвленной линейной RLC-цепи
и её основные параметры
При расчетах таких цепей для иллюстрации токов и напряжений на её идеализированных элементах используются временные и векторные диаграммы (рис. 3.5).
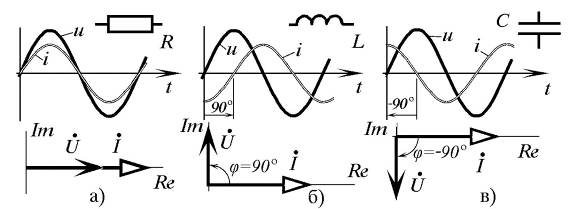
а) R–элемент б) L–элемент в) C–элемент
Рис. 3.5. Графики мгновенных значений напряжения, тока
и векторные диаграммы элементов цепи
Фазовые соотношения (фазовые сдвиги между синусоидальными электрическими величинами) не зависят от выбора момента начала отсчета времени, поэтому при построении векторных диаграмм любой один изображающий вектор можно совмещать с осью Re действительных чисел, а все остальные векторы наносить на диаграмму, строго выдерживая углы сдвига фаз.
Для расчета угла сдвига между фазой тока ψI и фазой напряжения ψU в последовательной RLC-цепи на основании параметров её элементов используется формула
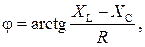
в которой величины XL = ωL = 2πfL и XC = 1/ωC = 1/2πfC называют соответственно реактивным индуктивным сопротивлением и реактивным емкостным сопротивлениям, а их разность X = XL – XC – реактивным сопротивлением цепи.
Зависимость между действующим током I и напряжением U, а также параметрами ω, R, L, С отдельных приемников определяется законом Ома для цепей синусоидального тока
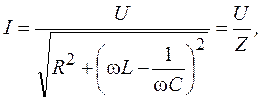
где знаменатель Z представляет собой полное сопротивление неразветвленной электрической RLC-цепи.
В зависимости от значений величин XL и XC угол сдвига фаз φбудет положительным, если XL > XC или отрицательным, если XL < XC. В первом случае преобладает индуктивная нагрузка, и ток при своем изменении во времени окажется отстающим от напряжения. Во втором случае преобладает емкостная нагрузка, и ток опережает напряжение.
Если в этой цепи выполняется равенство XL = XC, то полное сопротивление Z равно активному сопротивлению R, напряжение и ток совпадают по фазе, угол сдвига фаз φ равен нулю, коэффициент мощности цепи λ = cos φ= 1. Такое состояние называют резонансом напряжений. При этом частота собственных колебаний RLC-цепи, полное сопротивление и угол сдвига фаз соответственно равны
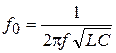 ;
; 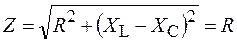 ;
; 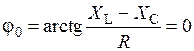 ,
,
а действующий ток достигает наибольшего значения (по этому значению экспериментально определяют состояние резонанса напряжения)
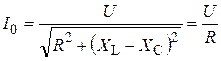 .
.
В RLC-цепи, у которой XL >> R << XC, в режиме резонанса напряжений действующие на реактивных элементах цепи напряжения, заметно больше напряжения U на зажимах исследуемой цепи (напряжение источника питания)
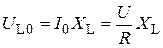 ;
; 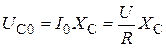 ,
,
что может оказаться причиной возникновения в реальном электротехническом устройстве аварийной ситуации (электрический пробой межвитковой изоляции в индуктивной катушке, пробой изоляции между обкладками конденсатора).
Мгновенная мощность в электрической цепи перемененного тока равна произведению мгновенных значений напряжения и тока
р = u i = Umsinωt Imsin(ωt±φ).
Среднее значение мощности Pср за период Т = 1/f, называемое активной мощностью Р, определяется по формуле
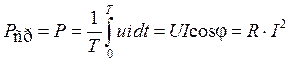 .
.
Реактивная Q и полная S мощности тока рассчитываются по формулам:
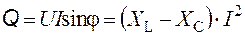 ;
; 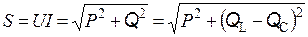 ,
,
где QL и QC – реактивные индуктивная и емкостная мощности тока.
По результатам прямых измерений напряжения на входе цепи U, падений напряжения на резисторе UR, индуктивной катушке UK, конденсаторе UC, тока I и активной мощности тока P расчет последовательной RLC-цепи можно выполнить по следующим формулам.
Полное сопротивление цепи
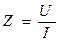 .
.
Полное сопротивление исследуемой цепи (рис. 3.3)
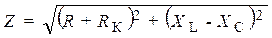 .
.
Активное суммарное сопротивление цепи
 .
.
Активное сопротивление резистора
 .
.
Полное, активное, реактивное сопротивления и индуктивность катушки:
 ;
; 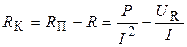 ;
; 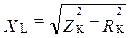 ;
; 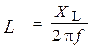 .
.
Реактивное сопротивление и емкость конденсатора:
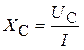 ;
; 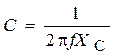 .
.
Полная и реактивная мощности тока цепи:
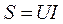 ;
; 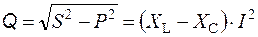 .
.
Коэффициент мощности тока цепи
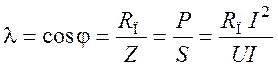 .
.
Графоаналитический расчет электрических цепи синусоидального тока выполняется с помощью векторных диаграмм. Их построение для цепей с последовательным соединением элементов R, L, C начинают с вектора тока I, относительно которого в выбранном масштабе строят векторы напряжений UR, UС, UK и U. При этом используется уравнение второго закона Кирхгофа в комплексной (векторной) форме
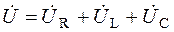 .
.
На рисунке 3.6 представлены векторные диаграммы электрических цепей с последовательным соединением: а – резистора и реальной катушки, б – резистора и конденсатора, в – резистора, конденсатора и реальной катушки.
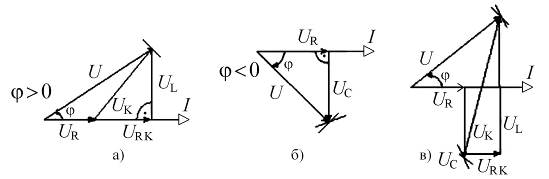
Рис. 3.6. Примеры построения векторных диаграмм напряжений и тока
последовательных цепей (метод засечек)
Разложение вектора падения напряжения UK на активную URK и реактивную UL составляющие (рис. 3.6а) позволяет непосредственно по векторной диаграмме реальной катушки определить ее параметры
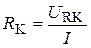 ;
; 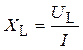 .
.
Дата добавления: 2016-03-20; просмотров: 1497;
