Результаты аналитических расчетов.

5.5 Сводка основных формул (методики расчета)

Трехфазной называется электрическая цепь, в различных ветвях которой действуют три одинаковые по амплитуде синусоидальные э.д.с., имеющие одну и ту же частоту и сдвинутые по фазе одна относительно другой на угол 2p/3 (120°).

Трехфазную нагрузку, соединенную звездой, подключают к генератору или трансформатору линейными проводами «А», «В», «С» и нейтральным проводом «0» (рис. 5.2). В трехфазных четырехпроводных цепях нейтральный провод заземляют и называют «нулевым».

Рис. 5.2. Трехфазная электрическая цепь с нагрузкой типа «Y»

Действующие напряжения U_AB, U_BC, U_CA между соответствующими линейными проводами называют линейными, а действующие напряжения U_A, U_B, U_C между соответствующими линейными и нулевым проводами называют фазными. Эти напряжения связаны между собой векторными уравнениями:

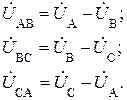
Если полные сопротивления 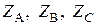отдельных приемников равны между собой

и углы j_A, j_B, j_C сдвига фаз между фазными напряжениями и соответствующими им фазными токами одинаковы

j_A = j_B = j_C,

то такую нагрузку называют симметричной.

Симметричный режим трехфазной цепи, соединенной звездой, характеризуется тем, что ток в нулевом проводе равен нулю, а при небольшой асимметрии намного меньше фазных токов. Это позволяет в питающем кабеле его жилу делать меньшего сечения, чем жилы линейных проводов. Между линейными и фазными напряжениями существует зависимость

.

Линейные токи I_Л являются одновременно и токами приемников соответствующих фаз, т.е. фазовыми токами I_Ф. Они равны между собой и сдвинуты по отношению к своим напряжениям на одинаковые углы.

j_Ф = arctg Х_Ф/R_Ф = arccos R_Ф/Z_Ф = arcsin Х_Ф/Z_Ф,

где Z_Ф – полное сопротивление фазной нагрузки; Х_Ф – реактивное сопротивление фазной нагрузки; R_Ф – активное сопротивление фазной нагрузки.

Симметричный режим трехфазной цепи, соединенной звездой, характеризуется векторными диаграммами напряжения и токов, как показано на рис. 5.3.

Рис. 5.3. Примеры векторных диаграмм токов и напряжений

симметричного режима работы трехфазной электрической цепи

с резистивно-индуктивными (а) и емкостными (б) приемниками,

соединенными звездой

По диаграммам видно, что суммы векторов фазных токов I_A, I_B, I_C равны нулю (геометрическое изображение их суммы представляет равносторонний треугольник).

При несимметричном режиме трехфазной сети не соблюдаются какое-либо одно или оба вместе равенства

и j _A = j _B = j _C.

При несимметричной нагрузке фаз нарушается симметрия фазных токов I_A, I_B, I_C и в нейтральном проводе возникает ток. Его можно определить графоаналитическим методом, исходя из векторного уравнения (первый закон Кирхгофа):

.

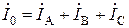При наличии нейтрального провода, если пренебречь небольшими различными падениями напряжения в подводящих проводах из-за неравенства токов в них, приемники находятся под одинаковыми величинами действующих фазных напряжений

U_A @ U_B @ U_C,

т.е. нейтральный провод обеспечивает симметричностьфазных напряжений. При наличии нейтрального провода для приемников, присоединенных к неповрежденным линейным проводам, обрыв «чужого» линейного провода практически не ощущается.

При обрыве нейтрального провода режим работы трехфазной несимметричной нагрузки значительно изменяется – фазные токи устанавливаются такими, чтобы их векторная сумма равнялась нулю. Это приводит к резкому искажению симметрии фазных напряжений. По этой причине плавкие предохранители и выключатели в нейтральном проводе нельзя ставить. В этом случае при обрыве линейного провода приемники соответствующей фазы потребителя остаются без энергии, а приемники двух других фаз продолжают получать питание от неповрежденных проводов трехфазной системы. При обрыве нейтрального провода фазные напряжения на зажимах обоих последовательно соединенных приемников пропорциональны величинам их полных сопротивлений, а при преобладании в одной фазе индуктивной, а в другой – емкостной нагрузки может возникнуть резонанс напряжений, сопровождающийся установлением повышенных напряжений на зажимах приемников и резким увеличением тока.

На рисунке 5.4 представлены диаграммы для трехфазной несимметричной индуктивно-емкостной нагрузки при наличии (а) и отсутствии (б) нейтрального провода, а также диаграммы несимметричной активной трехфазной нагрузки с оборванным линейным проводом фазы «А» при наличии (в) и отсутствии (г) нейтрального провода.

Векторные диаграммы строят циркулем в выбранном масштабе по опытным данным методом засечек. Сначала вычерчивают равносторонний треугольник линейных напряжений U_AB, U_BC, U_CA, затем из соответствующих его вершин радиусами, равными фазным напряжениям U_A, U_В, U_C описывают дуги, пересечение которых определяет точку, являющуюся началом векторов фазных напряжений. Под углами j_A = j_B = j_C к векторам фазных напряжений U_A, U_В, U_C проводят векторы фазных токов I_A, I_B, I_C. Пунктирными линиями на диаграммах обозначены соответствующие напряжения источника.

Построение векторных диаграмм основывается на системе векторных уравнений, связывающих линейные и фазные напряжения, нулевой ток и фазные токи приемника, т.е.

а также на векторных уравнениях связывающих фазные напряжения приемника U_A, U_B, U_C с фазными напряжениями источника U_a, U_b, U_c и напряжением U₀ между нулевыми точками приемника и источника, т.е.

Рис. 5.4. Векторные диаграммы токов и напряжений несимметричных режимов

трехфазной цепи при соединении звездой

Расчет трехфазной электрической цепи с симметричной нагрузкой сводится к расчету одной фазы. Измерения активной мощности тока можно выполнить для одной фазы и полученный результат утроить

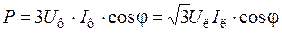, Вт.

При несимметричной нагрузке параметры каждой фазы рассчитываются отдельно методами, используемыми в расчетах однофазных цепей синусоидального тока. Трехфазная электрическая цепь рассматривается как разветвленная цепь с тремя источниками питания

;

.

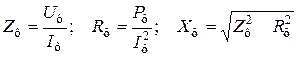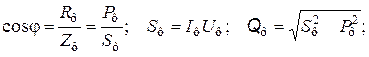
Активную мощность тока всех приемников, соединенных звездой, подсчитывают по формуле P = P_A + P_B + P_C и измеряют ваттметром в каждой фазе приемника.

При отсутствии нулевого провода активная мощность тока трехфазной электрической цепи измеряется двумя ваттметрами (рис. 5.5а), токовые катушки которых включены в линейные провода с токами I_A и I_C, а катушки напряжения – соответственно на линейные напряжения U_AB и U_BC. В соответствии с векторной диаграммой (рис. 5.5б) среднюю, т.е. активную мощность, выраженную через действующие напряжения и токи, определяют из выражения

,

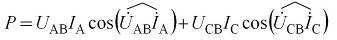где – угол между векторами линейного напряжения U_AB и тока фазы I_A; 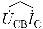– угол между векторами линейного напряжения U_CB и тока фазы I_C.

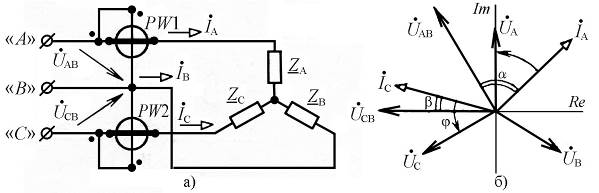
Рис. 5.5. Измерение активной мощности в трехпроводной цепи

методом двух ваттметров

Для расчета несимметричной трехфазной нагрузки, соединенной по схеме «звезда», может быть применен метод узлового напряжения в комплексной форме.

Напряжение между нулевыми точками (нейтралями) приемника и источника определяется выражением

где 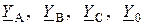– полные комплексные проводимости фаз и нулевого провода (если нулевой провод отсутствует, то Y₀=0); , , – комплексные фазные напряжения источника; , , – комплексные напряжения и токи в фазах приемника; , – полные комплексные сопротивления фаз приемника.

Полные комплексные сопротивления и мощности тока, а также активные и реактивные сопротивления и мощности тока отдельных фаз определяют по формулам:

;

,

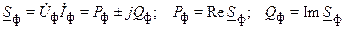где 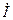– сопряженный комплексный ток; Re, Im – символы действительной и мнимой частей комплексной величины.

Трехфазная цепь с приемниками,