Результаты расчетов параметров переходных процессов
(косвенные измерения)
| Код замера | Параметры | |||||||
| t1, с | t2, с | Постоянная времени | Iпр, А | Uпр, В | ||||
| из опыта | расчёт | |||||||
| t1,С | t2,С | t1,С | t2,С | |||||
| о1-1 | ▒▒ | ▒▒ | ▒▒ | ▒▒ | ▒▒ | ▒▒ | ||
| о1-2 | ▒▒ | ▒▒ | ▒▒ | ▒▒ | ▒▒ | ▒▒ | ||
| о1-3 | ▒▒ | ▒▒ | ▒▒ | ▒▒ | ▒▒ | ▒▒ | ||
| о2-1 | ||||||||
| о2-2 | ||||||||
| о3-1 | ||||||||
| о3-2 | ||||||||
8.4.4 Исследовать переходной процесс в электрической цепи, содержащей ветвь с последовательным соединением резистора R и конденсатора С (опыт № 2).
Данный этап исследования выполняется в следующей последовательности:
1) подключить выводы Х9 и Х10 осциллографа PG (режим открытого входа « 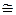 ») к контрольным выводам Х7 и Х8 участка w исследуемой цепи с конденсатором, значение ёмкости которого задано преподавателем, и замкнуть ключи S1 и S2;
») к контрольным выводам Х7 и Х8 участка w исследуемой цепи с конденсатором, значение ёмкости которого задано преподавателем, и замкнуть ключи S1 и S2;
2) установить частоту импульсов генератора UZ, при которой длительности импульсов t1 и пауз t2 обеспечивают завершение переходного процесса (выполаживание графика напряжения UC) (рис. 8.6б), и воспроизвести на «миллиметровке» в масштабе 1:2 график одного периода напряжения UC (UC1 и UC2), ориентируясь на координатную сетку экрана осциллографа (код замера о2-1);
3) уменьшить в два раза сопротивление резистора R и воспроизвести на «миллиметровке» в масштабе 1:2 график одного периода напряжения UC (UC1 и UC2), ориентируясь на координатную сетку экрана осциллографа (код замера о2-2);
4) произвести обработку данных опыта, последовательно произведя следующие действия:
− записать в таблицу 8.1 величины сопротивлений резисторов R0 и R в омах, ёмкости конденсатора С в микрофарадах, установившейся высоты импульса Y, протяженность импульса XИ, протяженность паузы XП в мм, цены деления шкалы экрана по вертикали α в В/мм, цены деления шкалы экрана по горизонтали β в с/мм;
− вычислить для каждого замера значения длительности импульсов t1 и пауз t2, установившихся значений напряжений амплитуд импульсов UС1, постоянных времени τ1 и τ2, результаты вычислений записать в таблицу 8.2.
8.4.5 Исследовать переходной процесс в электрической цепи, содержащей ветвь с последовательным соединением резистора R и катушки индуктивности L (опыт № 3).
Данный этап исследования выполняется в следующей последовательности:
1) подключить выводы Х9 и Х10 осциллографа PG (режим открытого входа « 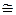 ») к контрольным выводам Х7 и Х8 участка v исследуемой цепи с катушкой индуктивности, значение активного сопротивления которой задано преподавателем, и замкнуть ключи S1 и S3;
») к контрольным выводам Х7 и Х8 участка v исследуемой цепи с катушкой индуктивности, значение активного сопротивления которой задано преподавателем, и замкнуть ключи S1 и S3;
2) установить частоту импульсов генератора UZ, при которой длительности импульсов t1 и пауз t2 обеспечивают завершение переходного процесса (выполаживание графика напряжения UL) (рис. 8.5б), и воспроизвести на «миллиметровке» в масштабе 1:2 график одного периода напряжения UL (UL1 и UL2), ориентируясь на координатную сетку экрана осциллографа (код замера о3-1);
3) уменьшить в два раза сопротивление резистора R и воспроизвести на «миллиметровке» в масштабе 1:2 график одного периода напряжения UL (UL1 и UL2), ориентируясь на координатную сетку экрана осциллографа (код замера о3-2);
4) произвести обработку данных опыта, последовательно произведя следующие действия:
− записать в таблицу 8.1 величины сопротивления резистора R0 и суммы сопротивления резистора R и активного сопротивления катушки индуктивности RK в омах, индуктивности катушки L в генри, установившейся высоты импульса Y, протяженность импульса XИ, протяженность паузы XП в мм, цены деления шкалы экрана по вертикали α в В/мм, цены деления шкалы экрана по горизонтали β в с/мм;
− вычислить для каждого замера значения длительности импульсов t1 и пауз t2, установившихся значений напряжений амплитуд импульсов UL1, постоянных времени τ1 и τ2, результаты вычислений записать в таблицу 8.2.
8.4.6 Для указанных преподавателем замеров рассчитать:
− значения принуждённых составляющих тока Iпр и напряжения Uпр;
− написать уравнения переходных процессов.
8.4.7 Сделать выводы по работе и ответить на контрольные вопросы.
8.5 Сводка основных формул (методики расчета)
Переходные или не установившиеся процессы возникают при переходе от одного установившегося состояния электрической цепи к другому при включении, скачкообразном изменении величины напряжения или самих параметров цепи, коротком замыкании и т.п. событиях.
Для расчета переходных процессов используются дифференциальные уравнения, составленные в соответствии с законами Кирхгофа для мгновенных значений токов и напряжений. При решении такого уравнения находят частное решение, когда переходной процесс закончен, и общее решение без правой части уравнения при отсутствии внешнего источника энергии, что соответствует свободному режиму.
Суммы установившихся и свободных токов и напряжений определяют токи и напряжения во время переходного процесса:
iпер = iу + iсв и uпер = uу + uсв.
Первый закон коммутации. Ток в ветви с индуктивным элементом не может изменяться скачком.
Второй закон коммутации. Напряжение на емкостном элементе не может изменяться скачком.
Переходные процессы не могут протекать мгновенно, так как невозможны мгновенные изменения энергии, запасённые в электрическом поле конденсатора и магнитном поле индуктивной катушки, соответственно равных
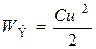 ,
, 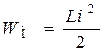 .
.
Из невозможности мгновенного изменения энергии на конечную величину следует, что при переходном процессе напряжение UС на зажимах конденсатора и ток IL в индуктивной катушке могут изменяться только непрерывно, без скачков. Это определяет начальные условия для UС и IL при переходных процессах. Вместе с тем возможны скачки тока в конденсаторе и напряжения на индуктивной катушке, а также скачки тока и напряжения на резисторе.
Длительность переходных процессов зависит от численных значений параметров (сопротивления резистора R, ёмкости конденсатора С, индуктивности катушки L) цепи, а напряжения и токи в переходном режиме могут быть большими по сравнению с этими величинами при установившемся режиме.
Для расчёта переходных процессов в электрических цепях составляют систему управлений по законам Ома и Кирхгофа для мгновенных значений напряжений и токов. Эту систему приводят к одному уравнению для одного параметра – напряжения или тока, которое в общем случае для линейных цепей будет обыкновенным линейным дифференциальным уравнением.
Например, для цепи с последовательным соединением элементов R, L, C (рис. 8.4) на основании второго закона Кирхгофа можно записать:
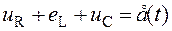 .
.
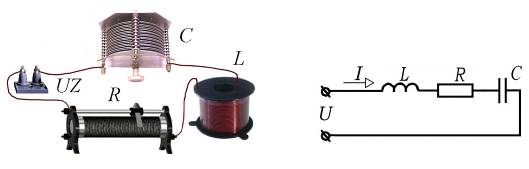
Рис. 8.4. Последовательная RLC-цепь
Или в дифференциальной форме:
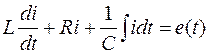 .
.
После дифференцирования получаем:
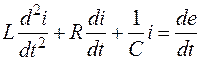 .
.
Известно, что полный интеграл такого уравнения есть его решение и равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Частное решение неоднородного уравнения выражает так называемый принуждённый режим, задаваемый источником.
Общее решение однородного уравнения показывает поведение цепи при отсутствии внешних источников энергии. Составляющие токов и напряжений, определяемые этим решением, называют свободными.
Для рассматриваемого примера однородное дифференциальное уравнение имеет вид:
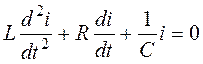 .
.
Его характеристическое уравнение:
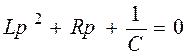 .
.
После отыскания корней характеристического уравнения р1 и р2 решение для свободной составляющей тока записывается как:
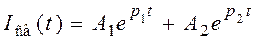 ,
,
где А1 и А2 – постоянные интегрирования, которые определяют из начальных условий.
При длительности процесса, когда t"∞, в цепи установится принуждённый (установившийся) ток IПР, т.е.
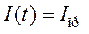 .
.
Свободная составляющая тока затухает и при t = ∞ и станет равна
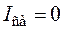 .
.
Полный переходной ток цепи равен сумме свободного и принуждённого токов
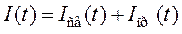 .
.
Таким образом, методика расчёта переходных процессов, называемая классической, состоит в составлении дифференциальных уравнений для цепи, их решения и определения постоянных интегрирования из начальных условий.
Экспериментальное исследование переходных процессов в электрических цепях выполняют при помощи электронного осциллографа. Исследуемую цепь присоединяют к генератору периодических прямоугольных импульсов напряжения длительностью t, превышающей время практического существования переходного процесса (рис. 8.2). Это позволяет при включении цепи на напряжение U = const в течение времени t1 наблюдать на экране осциллографа кривые изменения переходных напряжений и тока в цепи с последовательным соединением элементов R и L (рис. 8.2а-в), либо R и С (рис. 8.2г-е). В течение времени t2, когда напряжение U = 0, наблюдают аналогичные кривые при замыкании тех же цепей на резисторе с сопротивлением R0.
Цепь с последовательным соединением резистора R и катушки с индуктивностью L и активным сопротивлением RK, включённая на постоянное напряжение, описывается дифференциальным уравнением
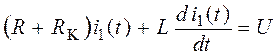 ,
,
решением которого является функция тока переходного процесса
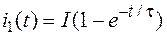 ,
,
где τ = L/(R + RK) – постоянная времени цепи с резистором R и катушкой L, с; 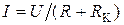 – ток принуждённого режима, А.
– ток принуждённого режима, А.
Из уравнения и кривой (рис. 8.5в) переходного процесса i(t) видно, что при прямоугольном импульсном напряжении (рис. 8.5б) в ветви цепи c последовательным соединением резистора R и катушки индуктивности L возникает переходной ток i1, изменяющийся по экспоненциальной кривой от нуля и асимптотически стремящийся к своему принуждённому значению.
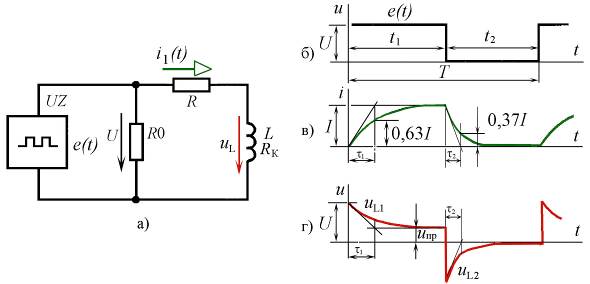
Рис. 8.5. Последовательная RL-цепь
В течение паузы между импульсами длительностью t2 > 5t2 в электрическую цепь не поступает энергия от генератора (режим замыкания RL-цепи на резистор R0) и переходный процесс описывается дифференциальным уравнением
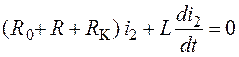 .
.
Решая это уравнение, находим переходный ток в контуре
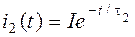 .
.
Этот ток существует за счёт предварительно накопленной энергии в магнитном поле индуктивной катушки. Он затухает по экспоненциальной кривой и практически прекращается спустя время равное 5t2.
Постоянные времени t1 и t2 определяются длиной подкасательных к соответствующим кривым i1(t1) и i2(t2).
В установившемся режиме падение напряжения на катушке индуктивности отлично от нуля (UПР > 0) из-за активного сопротивления провода обмотки.
Цепь с последовательным соединением резистора R и конденсатора С, включённая на постоянное напряжение, описывается дифференциальным уравнением
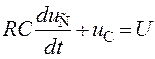 ,
,
решением которого является функция переходного напряжения на зажимах конденсатора
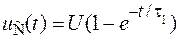 .
.
Переходной ток определяется по формуле:
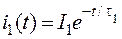 ,
,
где t1 = RC – постоянная времени, с; I1 = U/R – значение переходного тока в момент включения цепи на напряжение U.
Из уравнений и кривых (рис. 8.6) переходного процесса UС(t) и i1(t) видно, что включение цепи с резистором R и конденсатором С на напряжение U = const вызывает появление в цепи переходного напряжения UC(t) на зажимах конденсатора и переходного тока i1(t), изменяющихся по экспоненциальным кривым. Напряжение постепенно возрастает от нуля и асимптотически приближается к своему принужденному значению U, а ток мгновенно принявший в момент включения величину U/R, убывает по экспоненте и стремится к нулевому значению.
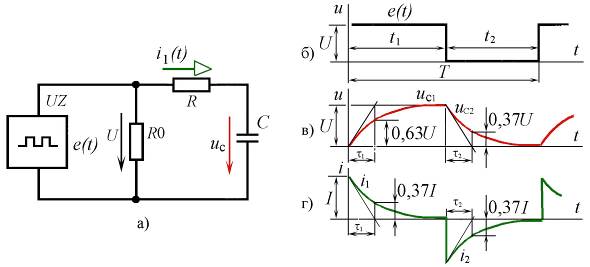
Рис. 8.6. Последовательная RС-цепь
В течение паузы длительностью t2 ³ 5t2 в электрическую цепь не поступает энергия от генератора (замыкание RС-цепи на резистор R0), переходный процесс описывается дифференциальным уравнением
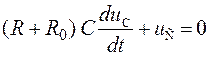 .
.
Решая это уравнение, находим переходное напряжение на зажимах конденсатора
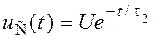 ,
,
а также переходный ток в контуре
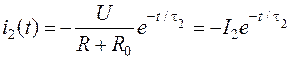 .
.
Из уравнений и кривых (рис. 8.6в, г) переходных процессов uС(t) и i2(t) видно, что при замыкании на резистор заряженного конденсатора кривая тока его заряда носит затухающий характер, в результате чего UС(t)®0 и i2(t)®0.
Постоянные времени t1 и t2 находят из соответствующих осциллограмм переходных напряжений на зажимах конденсатора или индуктивной катушки. Для точного проведения касательных к кривым с нарастающим значением напряжения или тока следует наносить ординату, равную 0,63 принуждённого значения соответствующей величины, а для кривых с убывающим значением напряжения или тока – ординату, составляющую 0,37 принуждённого значения той же величины до возникновения переходного процесса.
Определение принуждённых значений напряжений на зажимах конденсатора и тока в цепи (по напряжению на зажимах резистора с известной величиной его сопротивления), производится осциллографом с использованием его чувствительности по напряжению a=В/мм:
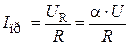 ;
; 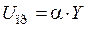 ,
,
где UR – максимальное напряжение, замеренное на резисторе, В; Y – максимальное отклонение луча осциллографа по вертикали от нулевого положения, мм; a - чувствительность осциллографа по напряжению, В/мм определяют путём подачи на вход осциллографа эталонного напряжения.
Определение длительности прямоугольных импульсов по осциллограмме производится на основе известной частоты развертки осциллографа. Если на экране имеется изображение, соответствующее периоду импульсов осциллограммы (рис. 8.3), то частота развёртки осциллографа совпадает с частотой импульсов генератора. Следовательно:
Т = 1/f0 , T=t1+t2.
Магнитные цепи переменного тока
9.4.1 Ознакомиться с приборами, аппаратами и другим оборудованием экспериментальной установки и записать их технические характеристики в отчет.
9.4.2 Измерение геометрических параметров магнитопровода и определение его расчетных параметров (опыт № 1).
Данный этап исследования выполняется в следующей последовательности:
1) штангенциркулем измеряются размеры сердечника магнитопровода, указанные на эскизе (рис. 9.1);
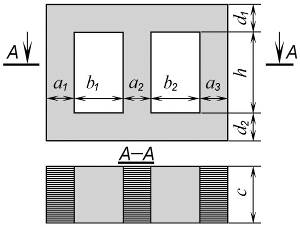
Рис. 9.1. Эскиз магнитопровода
2) по результатам измерений рассчитываются площади сечений Si и протяженность средних линий li всех участков магнитопровода (рис. 9.2 а). Результаты измерения и расчетов вносятся в таблицу 9.1;
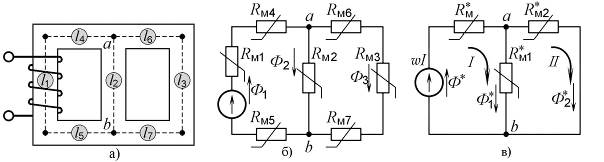
Рис. 9.2. Разветвленная магнитная цепь и её расчетные схемы
Таблица 9.1
Дата добавления: 2016-03-20; просмотров: 1699;
