Соединенными треугольником
6.4.1 Ознакомиться с приборами, аппаратами и прочим оборудованием экспериментальной установки и записать их технические характеристики в протокол испытания.
6.4.2 Собрать электрическую цепь по схеме, приведенной на рисунке 6.1.
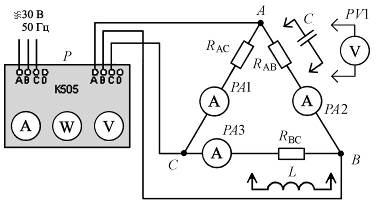
Рис. 6.1. Принципиальная электрическая схема экспериментальной установки
6.4.3 Измерить параметры трехфазной цепи при симметричной активной нагрузке в фазах (RAB = RBC = RAC) (опыт № 1).
Данный этап исследования выполняется в следующей последовательности:
1) после проверки руководителем правильности соединений включить источник питания;
2) с помощью измерительного комплекта К 505 выполнить измерение следующих величин:
– линейных токов IA, IB, IC;
3) с помощью амперметров PA1, PA2, PA3 и вольтметра PV1 выполнить измерение следующих величин:
– фазных напряжений UAB, UBC, UCA;
– фазных токов IAB, IBC, ICA.
Результаты измерений записать в таблицу 6.1.
Таблица 6.1
Результаты экспериментальных измерений
| IA, А | IB, А | IC, А | IAB, А | IBC, А | ICA, А | UAB, В | UBC, В | UCA, В |
6.4.4 Измерить параметры трехфазной цепи при несимметричной активно-индуктивно-емкостной нагрузках в фазах (опыт № 2).
Данный этап исследования выполняется в следующей последовательности:
1) резистор RВС заменить индуктивной катушкой L, а резистор RАС заменить конденсатором C;
2) после проверки руководителем правильности соединений включить источник питания;
3) с помощью измерительного комплекта К 505 выполнить измерение следующих величин:
– линейных токов IA, IB, IC;
4) с помощью амперметров PA1, PA2, PA3 и вольтметра PV1 выполнить измерение следующих величин:
– фазных напряжений UAB, UBC, UCA;
– фазных токов IAB, IBC, ICA.
Результаты измерений записать в таблицу 6.1.
6.4.5 Используя графоаналитический метод произвести анализ режимов работы трехфазной цепь с приемниками соединенными треугольником при симметричной и несимметричной нагрузке.
Данный этап исследования выполняется в следующей последовательности:
1) построить по опытным данным (табл. 6.1) две векторные диаграммы напряжений и токов методом засечек (рис. 6.3 и 6.4).
2) транспортиром измерить у векторных диаграмм углы сдвига фаз между фазными токами и фазными напряжениями jAB, jBC, jCA;
3) вычислить величины активных RAB, RBC и реактивных XAB, XBC сопротивлений, а также активные фазные мощности тока PAB, PBC.
Результаты расчетов записать в таблицу 6.2;
Таблица 6.2
Результаты аналитических расчетов
| jAB, гр | jBC, гр | jCA, гр | PAB, Вт | PBC, Вт | RAB, Вт | RBC, Вт | XBС, Ом | XСA, Ом |
4) на основании табличных данных и векторных диаграмм сделайте выводы об особенностях работы трехфазной цепи при симметричной активной и несимметричной активно-индуктивно-емкостной нагрузке, приёмники фаз которой соединены треугольником. Ответить на контрольные вопросы.
6.5 Сводка основных формул (методики расчета)
Три мгновенных синусоидальных напряжения между соответствующими линейными проводами A, B, C трехфазной трехпроводной сети имеющих одинаковые амплитуды Um
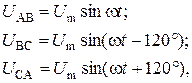
сдвинутые по фазе относительно друг друга на угол a = 120° и изменяющиеся во времени с частотой f = w/2p, образуют симметричную трехфазную систему напряжений.
На рисунке 6.2 представлена схема включения в трехфазную сеть соединения токоприемников треугольником. Каждый приемник находится под линейным напряжением Uл, которое одновременно является фазным напряжением Uф, т.е. Uф = Uл.
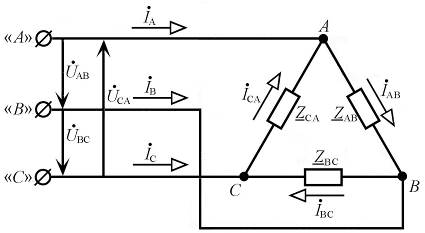
Рис. 6.2. Трехфазная электрическая цепь с приемниками,
соединенными треугольником
Ток каждого приемника, входящий в соединение треугольником, является фазным и определяется по формуле
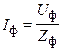 ,
,
где Zф – полное сопротивление фазы.
В общем случае линейные токи IA, IB, IC, в проводах A, B и C определяются геометрической разностью соответствующих фазных токов IAB, IBC, ICA приемников и связаны векторными уравнениями
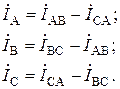
Из этих уравнений вытекает то, что независимо от характера нагрузки (симметричная или несимметричная) всегда справедливо равенство
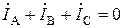 .
.
При симметричной нагрузке полные сопротивления фаз ZAB, ZBC, ZCA равны между собой, углы jAB, jBC, jCA сдвига фаз между фазными напряжениями и соответствующими им фазными токами одинаковы. Значения этих углов определяют из выражения
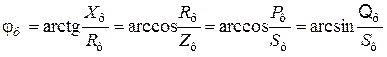
где Rф – активное сопротивление фазы; Xф – реактивное сопротивление фазы; Zф – полное сопротивление фазы; Pф, Qф, Sф – активная, реактивная и полная мощности тока фазы.
При симметричной нагрузке все линейные токи равны между собой и превышают значение фазных токов в  раз, т.е.
раз, т.е.
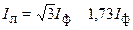 .
.
На рисунке 6.3 представлены топографическая и векторная диаграммы напряжений и токов для соединения приемников треугольником при симметричной активно-индуктивной нагрузке (типичная ситуация для электропотребителей на производстве) в фазах и показан графический способ нахождения линейных токов IA, IB, IC по фазным токам нагрузки.
Из диаграмм видно, что все линейные токи отстают от соответствующих фазных токов на угол 30°; линейные и фазные токи в отдельности сдвинуты по фазе относительно друг друга на угол 120°.
Несимметричная нагрузка фаз характеризуется неравенством полных сопротивлений в фазах и сдвигов фаз между фазными напряжениями и токами, при этом нарушается симметрия как фазных, так и линейных токов. Всякое изменение нагрузки в одной из фаз вызывает одновременное изменение соответствующих фазного и двух линейных токов и не влияет на величины фазных напряжений и токов других фаз, а также на величину третьего линейного тока.
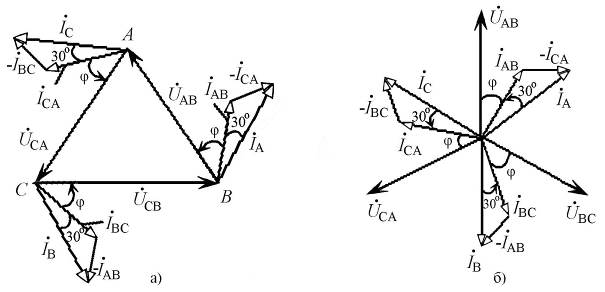
Рис. 6.3. Топографическая и векторная диаграммы токов и напряжений
симметричного режима трехфазной цепи при соединении
элетроприемников треугольником
На рисунке 6.4 представлена диаграмма напряжений и токов для соединения приемников треугольником при несимметричном режиме для случая, когда в фазе AB активная нагрузка (jAB = 0), в фазе BC – активно-индуктивная (jBC > 0), в фазе CA – емкостная (jCA = - 90°).
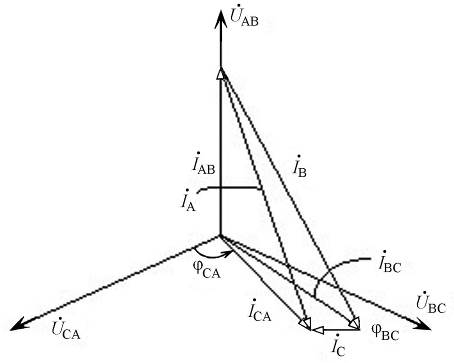
Рис. 6.4. Векторная диаграмма токов и напряжений несимметричного
режима трехфазной цепи при соединении треугольником
Построение такой векторной диаграммы циркулем в масштабе методом засечек выполняют в следующей последовательности.
Строят координатные оси под углами 120°. По координатным осям направляют векторы фазных напряжений UAB, UBC, UCA, которые без учета падения напряжения на внутренних сопротивлениях источника и в подводящих проводах остаются симметричными. Так как нагрузкой фазы AB является резистор, то по направлению вектора UAB строят вектор фазного тока IAB. Учитывая, что нагрузкой в фазе CA является конденсатор, вектор фазного тока ICA строят с опережением на 90° относительно вектора фазного напряжения UCA. Соединив концы векторов IAB и ICA, получают вектор линейного тока IA, который связан с фазными токами IAB и ICA векторным уравнением
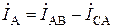 .
.
Векторная сумма линейных токов IA, IB, IC при любой нагрузке равна нулю, т.е.
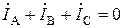 ,
,
и образует замкнутый треугольник векторов.
На основании этого, используя построенный вектор линейного тока IA, строят с помощью циркуля треугольник векторов линейных токов. Наконец, соединив начало диаграммы с точкой соединения векторов линейных токов IB, и IC, строят вектор фазного тока IBC.
Построение векторной диаграммы циркулем методом засечек при известных значениях линейных и фазных токов и характере нагрузки в фазах можно выполнить и в другой последовательности.
Вначале строят треугольник линейных токов, затем, используя известные геометрические соотношения между линейными и фазными токами, строят векторы фазных токов. Координатные оси и векторы фазных напряжений располагают относительно того вектора фазного тока, который обусловлен активной нагрузкой в фазе.
Обрыв одного из линейных проводов нарушает номинальный режим работы электроприемников. Приемники только одной фазы будут находиться под номинальным фазным напряжением. Приемники двух других фаз окажутся соединенными последовательно. Трехфазная цепь преобразуется в однофазную с двумя параллельными ветвями. Последовательно соединенные приемники окажутся под напряжением, отличающимся от номинального значения фазного напряжения. При наличии индуктивной катушки и конденсатора в этой ветви может возникнуть резонанс напряжений, сопровождающийся появлением повышенных напряжений на зажимах реактивных приемников и резким увеличением тока.
В этом случае построение векторных диаграмм циркулем методом засечки при известных значениях токов и угла сдвига фаз между фазным током и фазным напряжением неповрежденной фазы выполняют так же, как и для однофазной электрической цепи с параллельным соединением приемников.
Примерный вид векторных диаграмм токов и напряжения для исследуемой трехфазной несимметричной нагрузки, соединенной треугольником, при обрыве какого-либо одного линейного провода показаны на рисунке 6.5.
Угол сдвига фаз между током и напряжением неповрежденной фазы определяют аналитически по рассчитанным величинам полного, активного и реактивного сопротивления данной фазы.
Аналитический расчет величин сопротивлений и мощностей токов по известным значениям фазных токов и напряжений выполняют для каждой фазы в отдельности по формулам, используемым при аналогичных расчетах в однофазных цепях.
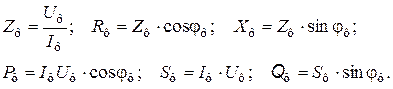
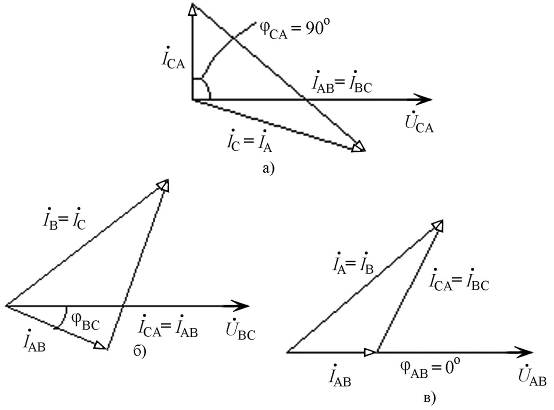
Рис. 6.5. Векторные диаграммы токов и напряжений трехфазной
несимметричной нагрузки, соединенной треугольником, при обрыве:
а) линейного проводника А, б) лининейного проводника В,
в) линейного проводника С
Угол сдвига фаз между токами и напряжениями в исследуемой трехфазной нагрузке измеряют транспортиром в построенных графически векторных диаграммах.
Электрическая цепь с нелинейными элементами
7.4.1 Ознакомиться с приборами, аппаратами и другим оборудованием экспериментальной установки и записать их основные технические характеристики в отчет.
7.4.2 Исследовать влияние величины напряжения на ток, потребляемую мощность и сопротивление в отдельности для каждой из двух ламп при различных значениях напряжения в диапазоне 0–240 В через каждые 20–30 В (опыт № 1).
Исследования проводить в следующей последовательности:
1) собрать электрическую схему согласно схеме (рис. 7.1) и после проверки преподавателем правильности соединений подключить тумблером S1 автотрансформатор T к сетевому напряжению 220 В;
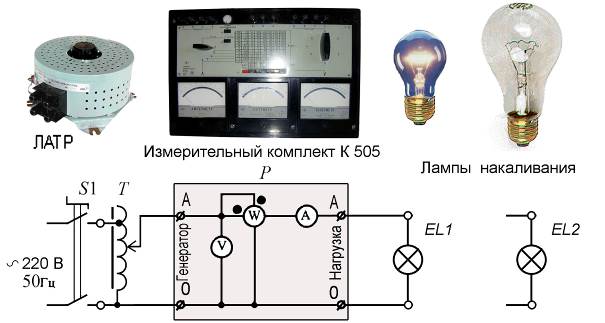
Рис. 7.1. Схема опыта № 1
2) записать показания амперметра, вольтметра и ваттметра комплекта К 505 и результаты расчета дифференциального сопротивления в таблицу 7.1;
Таблица 7.1
Дата добавления: 2016-03-20; просмотров: 3993;
