Правило расстановки индексов
1. а) Обратим внимание на знаки: для самопроизвольной реакции (т.е. реакции, идущей в прямом направлении)
 |
Положительный знак ∆ψрцозначает, что работа по перемещению единичного положительногозаряда от электрода 1 к электроду 2 совершалась бы надсистемой (п. 1.4); следовательно, перенос отрицательногозаряда (каковыми являются электроны) происходит в указанном направлении самойсистемой.
б) Отсюда вытекает следующая расстановка индексов в записи
 |
1 — восстановитель(донор электронов),
2 — окислитель(акцептор электронов).
в) Соответственно,
Ψ1 — электрический потенциал катода(–): здесь — избыток электронов;
Ψ2— электрический потенциал анода(+), на котором — дефицит электронов.
 |
2. а) Следовательно, обобщенную ОВР, за счет которой генерируется ЭДС в
гальваническом элементе, следует записать в виде
где фигурируют две окислительно-восстановительные пары (ОВ-пары):
- пара 1 (Ox1/Rd1)— служит в реакции восстановителем и образует катод,
- и пара 2(Ox2/Rd2)— служит окислителеми образует анод.
б) Заметим: в записи отдельной окислительно-восстановительной пары первой указывается окисленная форма.
3. В результате, например, для элемента Даниэля—Якоби (рис. 14.1 и (14.5))
необходимо полагать:
 |
поскольку в происходящей в этом элементе реакции первая из указанных пар
является восстановителем, а вторая — окислителем.
14.8. Зависимость ∆Ψрцот концентраций участников ОВР
И от температуры
1. Зависимость от концентраций.
а) Вспомним уравнение изотермы реакции:
 |
 |
которое определяет зависимость энергии Гиббса от концентраций (активностей) участников. Здесь ΔG°рц – стандартное значение этой энергии; оно соответствует реакции при постоянных одномолярных концентрациях всех реагентов и продуктов. А Па – произведение активностей, которое для обобщённой ОВР вида (14.14) равно:
б) Подставим (8.35,б) в формулу (14.12,б). Тогда получаем уравнение Нернста:
де
u
Здесь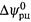 
— стандартная ЭДС реакции {стандартный электрический потенциал реакции). Эта величина, как иΔG°рц, соответствует ситуации, когда в полуэлементах поддерживаются одномолярные активности всех участников.
в) Вместе с тем, благодаря соотношению (4.35), стандартная ЭДС реакции просто связана с константой равновесия той же реакции (14.17,в).
г) Итак, уравнение Нернста (14.17,а) устанавливает зависимость ЭДС гальванического элемента от концентраций (активностей) участников ОВР.
Конкретно: чем меньшеПа, тем больше генерируемая ЭДС. Важно отметить, что при этом учитываются активности веществ в обоих полуэлементах.
2. Зависимость от температуры.
а) А здесь воспользуемся формулой (5.13, а)
 |
которая следует из соотношения
 |
при условии, что энтальпия и энтропия реакции практически не зависят от
температуры. Подстановка (14.17,б) дает:
б) Производная 
называется температурным коэффициентом ЭДС. Как видно, этот коэффициент полностью определяется энтропией реакции. Отсюда вытекает, что сама зависимость 
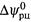от температуры является линейной.
 |
в) С другой стороны, измеряя ЭДС гальванического элемента при разных температурах, производную
можно оценить из экспериментальных данных. Тогда легко найти не только энтропию реакции (исходя из (14.18)), но и энтальпию, т.е. (вместе с энергией Гиббса (14.17,в)) все три термодинамические характеристики соответствующей ОВР. Действительно,
или
 |
г) Итак, чтобы воспользоваться данной формулой, надо знать производную
стандартной ЭДС по температуре, а также конкретное значение стандартной
ЭДС при какой-либо температуре.
Дата добавления: 2016-03-20; просмотров: 603;