Средняя квадратическая ошибка функций измеренных величин
Если мы имеем функцию суммы или разности двух независимых величин
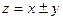 , (3.7)
, (3.7)
то квадрат средней квадратической ошибки функции выразится формулой:
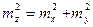 . (3.8)
. (3.8)
При 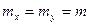
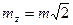 . (3.9)
. (3.9)
Пример. Линия на плане масштаба 1:5000 измерена по частям. Одна часть длиной 600,5 м, вторая часть длиной 400,0 м. Найти средние квадратические ошибки суммы и разности этих длин и соответствующие им относительные ошибки.
Решение. Средняя квадратическая ошибка суммы и разности двух длин будет 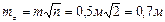 , где т = 0,5 м —точность масштаба. Относительные ошибка суммы и разности длин соответственно равны
, где т = 0,5 м —точность масштаба. Относительные ошибка суммы и разности длин соответственно равны
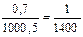 и
и 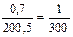
Если функция имеет вид
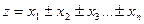 (3.10)
(3.10)
то
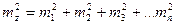 , (3.11)
, (3.11)
т. е. квадрат средней квадратической ошибки алгебраической суммы аргументов равен сумме квадратов средних квадратических ошибок слагаемых.
Если 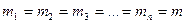 , то формула (4.11) примет вид
, то формула (4.11) примет вид
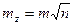 , (3.12)
, (3.12)
т. е. средняя квадратическая ошибка алгебраической суммы (разности) измеренных с одинаковой точностью величин в 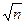 раз больше средней квадратической ошибки одного слагаемого.
раз больше средней квадратической ошибки одного слагаемого.
Пример. В шестиугольнике каждый угол измерен с одинаковой точностью 0,5', средняя квадратическая ошибка суммы всех измеренных углов будет
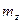 = 0,5'
= 0,5' 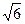 =1,2'.
=1,2'.
Если функция имеет вид
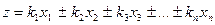 , (3.13)
, (3.13)
то
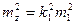
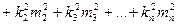 , (3.14)
, (3.14)
где k1, k2, k3, ..., kn — постоянные числа; 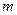 1,
1, 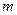 2,
2, 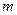 3, …
3, … 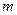 n, — средние квадратические ошибки соответствующих аргументов. Если имеем функцию многих независимых переменных общего вида
n, — средние квадратические ошибки соответствующих аргументов. Если имеем функцию многих независимых переменных общего вида
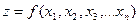 , (4.15)
, (4.15)
то
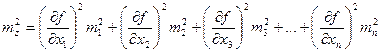 . (3.16)
. (3.16)
Из формулы (4.16) следует, что квадрат средней квадратической. ошибки функции общего вида равен сумме квадратов произведений частных производных по каждому аргументу на среднюю квадратическую ошибку соответствующего аргумента.
Пример. В цехе измерены длина, а =100,00 м со средней квадратической ошибкой 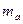 = 10 см и ширина
= 10 см и ширина
b = 20,00 м со средней квадратической ошибкой 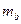 = 4 см. Найти среднюю квадратическую ошибку определения площади цеха.
= 4 см. Найти среднюю квадратическую ошибку определения площади цеха.
Ответ. Функция имеет вид П = аb.
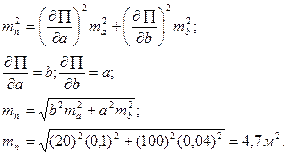
Дата добавления: 2016-03-15; просмотров: 4365;
