Классификация ошибок измерений
При геодезических измерениях неизбежны ошибки. Эти ошибки бываютгрубые, систематическиеислучайные. К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения. Систематические ошибки происходят от известного источника, имеют определенный знак и величину, их можно учесть при измерениях или вычислениях. Влияние систематических ошибок на результат измерений сводится к минимуму путем введения поправки к результату измерения или применением соответствующей методики измерений. Случайные ошибки имеют место при каждом измерении. Эти ошибки обусловлены точностью прибора, квалификацией наблюдателя, влиянием внешней среды, и полностью исключить их из результатов измерений нельзя. Закономерность таких ошибок проявляется лишь при большом числе измерений.
Так как случайные ошибки исключить из результатов измерений нельзя, то возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи можно разрешить с помощью теории ошибок измерений.
В основу теории ошибок положены следующие свойства случайных ошибок:
1. Малые ошибки встречаются чаще, а большие реже.
2. Ошибки не превышают известного предела.
3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине, одинаково часто встречаются.
4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе измерений.
Арифметическая средина. Средняя квадратическая ошибка. Предельная и относительная
Ошибки
Исходя из четвертого свойства случайных ошибок при геодезических измерениях одинаковой точности, за окончательный результат принимают среднее арифметическое из ряда измерений.
Если измерена одна и та же величина п раз и получены результаты: 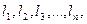 , то
, то
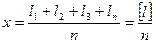 (3.1)
(3.1)
Величина х называется арифметической срединой или вероятнейшим значением измеренной величины.
Разности между каждым измерением и арифметической срединой называются вероятнейшими ошибками измерений:
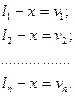 (3.2)
(3.2)
Сложив равенства (4.2), получим
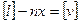 . (3.3)
. (3.3)
Из формул (4.1) и (4.3) следует, что 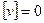 .
.
Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:
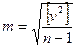 , (3.4)
, (3.4)
где 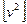 — сумма квадратов вероятнейших ошибок; п — число измерений.
— сумма квадратов вероятнейших ошибок; п — число измерений.
Средняя квадратическая ошибка арифметической средины вычисляется по формуле:
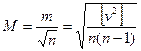 . (3.5)
. (3.5)
Предельная ошибка не превышает утроенной средней квадратической ошибки, т. е.
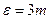 . (3.6)
. (3.6)
Пример. Пусть линия измерена шесть раз. Необходимо определить ее вероятнейшую длину и оценить точность этого результата. Все вычисления приведены в табл. 3.1.
Таблица 3.1
| № п.п | Длина линии, м. | V,см | V2 |
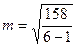 = 5,6 см = 5,6 см
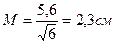
|
| 225,26 225,23 225,22 226,14 225,23 225,12 | +6 +3 +2 -6 +3 -8 | |||
| xср =225,20 | 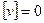
| 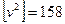
|
По формулам (4.4) и (4.5) вычислены абсолютные средние квадратические ошибки, а оценивать точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная ошибка вероятнейшего значения измеренной линии равна
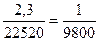 .
.
Дата добавления: 2016-03-15; просмотров: 1584;
