Алгоритм расчета критерия Розенбаума
1. В каждой из выборок должно быть не менее 11 наблюдений.
Объемы выборок должны примерно совпадать:
· При организации менее 50 наблюдений – разница не более 10;
· От 50 до 100 наблюдений – не больше 20;
· Если организовано более ста наблюдений, то одна из выборок не должна быть больше другой более чем в 1,5 – 2 раза.
2. Упорядочить значения отдельно в каждой выборке по степени возрастания признака.
Считать выборкой 1 ту выборку, значения в которой предположительно выше, а выборкой 2 – ту, где значения предположительно ниже.
3. Определить самое высокое (максимальное) значение в выборке 2.
4. Подсчитать количество значений в выборке 1, которые выше максимального значения в выборке 2. Обозначить полученную величину как S1.
5. Определить самое низкое (минимальное) значение в выборке 1.
6. Подсчитать количество значений в выборке 2, которые ниже минимального значения выборки 1. Обозначить полученную величину как S2.
7. Подсчитать эмпирическое значение Q по формуле: Q = S1 + S2.
8. По таблице определить критические значения Q для данных n1 и n2. Если Qэмп равно Q0,05 или превышает его, H0 отвергается.
Пример:
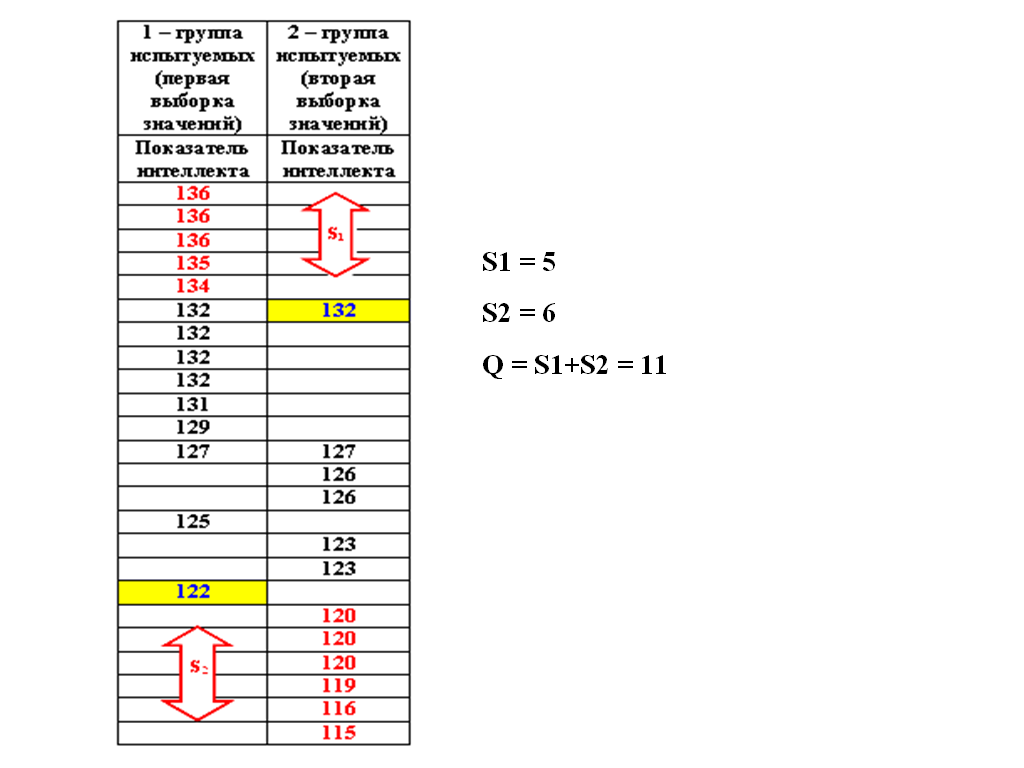
Алгоритм расчета критерия Манна-Уитни 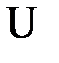
1. Пометить данные испытуемых выборки 1 одним цветом, скажем, красным, а все данные из выборки 2 – другим, например, синим.
2. Расположить все данные в единый ряд по степеням нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы была одна большая выборка.
3. Проранжировать значения, приписывая меньшему значению меньший ранг.
4. Вновь разделить данные на две группы, ориентируясь на цветные обозначения: красные данные в один ряд, синие – в другой.
5. Подсчитать сумму рангов отдельно по каждой выборке. Проверить, совпадает ли сумма рангов с расчетной.
6. Определить большую из двух ранговых сумм.
7. Определить по формуле значение
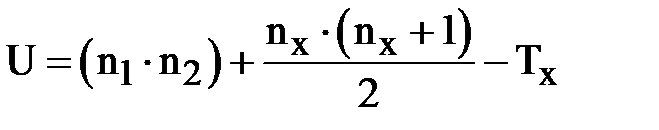 ,
,
где 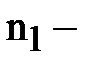 количество испытуемых в выборке 1;
количество испытуемых в выборке 1; 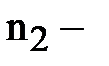 количество испытуемых в выборке 2;
количество испытуемых в выборке 2; 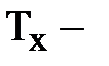 большая из двух ранговых сумм;
большая из двух ранговых сумм; 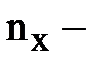 количество испытуемых в группе с большей суммой рангов.
количество испытуемых в группе с большей суммой рангов.
8. Определить критические значения 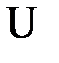 . Если
. Если 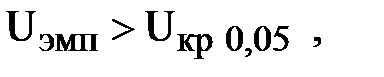 то гипотеза
то гипотеза 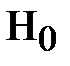 принимается. Если
принимается. Если 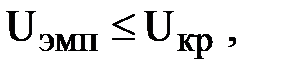 то отвергается. Чем меньше значения
то отвергается. Чем меньше значения 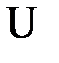 , тем достоверность различий выше.
, тем достоверность различий выше.
Пример:
Сравнить эффективность двух методов обучения в двух группах. Результаты испытаний представлены в таблице.

1. Перенесем все данные в другую таблицу, выделив данные второй группы подчеркиванием, и делаем ранжирование общей выборки.
| Значения | 7 | 8 | 10 | 10 | 14 | 15 | 15 | 16 | 19 | 20 | 29 | ||||||
| Ранги | 1,5 | 1,5 | 9,5 | 9,5 | 11,5 | 11,5 | |||||||||||
| Номер |
2. Найдем сумму рангов двух выборок и выберем большую из них: 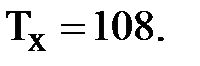
3. Рассчитаем эмпирическое значение критерия по формуле : 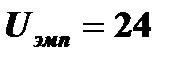
4. Определим критическое значение критерия при уровне значимости p≤0,05 U0,05=19
Вывод:так как расчетное значение критерия 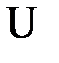 больше критического при уровне значимости
больше критического при уровне значимости 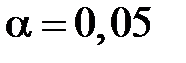 и
и 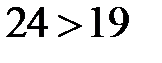 , гипотеза о равенстве средних принимается, различия в методиках обучения будут несущественны.
, гипотеза о равенстве средних принимается, различия в методиках обучения будут несущественны.
Дата добавления: 2016-03-05; просмотров: 4094;
