Задача оценки достоверности сдвига значений исследуемого признака
Алгоритм расчета критерия знаков 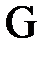
1. Подсчитать количество нулевых сдвигов и исключить их из рассмотрения. В результате 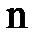 уменьшится на количество нулевых сдвигов.
уменьшится на количество нулевых сдвигов.
2. Определить преобладающее направление изменений. Считать сдвиги в преобладающем направлении «типичными».
3. Определить количество «нетипичных» сдвигов. Считать это число эмпирическим значением 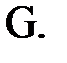
4. Определить критические значения 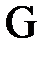 для данного
для данного 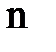 .
.
5. Сопоставить расчетное и критическое значения критерия 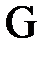 . Если расчетное значение критерия меньше критического, то сдвиг в типичную сторону может считаться достоверным.
. Если расчетное значение критерия меньше критического, то сдвиг в типичную сторону может считаться достоверным.
Пример:
В группе спасателей (n=15) был проведен тренинг по формированию стрессоустойчивости. Нужно оценить достоверность сдвига исследуемого параметра.
| N | |||||||||||||||
| До воздействия | |||||||||||||||
| После воздействия | |||||||||||||||
| Результат | + | + | + | + | + | + | + | = | + | + | + | – | + | + | – |
Количество сдвигов со знаком «+»=12 – типичный сдвиг в сторону повышения стрессоустойчивости. Количество сдвигов со знаком «–» = 2. Один сдвиг – «нулевой», поэтому n уменьшается до 14. По таблице определяем критические значения критерия знаков – 3 (p≤0,05) и 2 (p≤0,01).
Вывод: в результате проведения социально-психологического тренинга по формированию стрессоустойчивости в группе спасателей произошел сдвиг ее показателей в сторону повышения (G=2; p≤0,01;n=14).
T-критерий Вилкоксона. Этот критерий применяется для решения тех же задач, что и критерий знаков, но он позволяет оценить не только направление сдвига, но и его интенсивность. Он основан на подсчете суммы рангов значений сдвигов случайной величины с более редким (или менее ожидаемым) знаком:
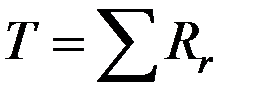 ,
,
при этом – чем меньше полученное значение T-критерия, тем более вероятно, что интенсивность типичного сдвига превосходит интенсивность нетипичного.
Дата добавления: 2016-03-05; просмотров: 1814;
