Критерий устойчивости Михайлова
Этот критерий устойчивости разработан А. В. Михайловым в 1938 г [10].
Для устойчивой системы годограф характеристического вектора порядка n, начинаясь на действительной положительной полуоси комплексной плоскости, при изменении ω от 0 до ∞ последовательно охватывает в положительном (против часовой стрелки) направлении n квадратов комплексной плоскости.
 |
На рис. 4.5 представлены годографы устойчивых систем различных порядков. На рис. 4.6 показаны годографы устойчивой (график 1), неустойчивой (график 3) и нейтральной систем (график 2 проходит через начало координат – границу устойчивости).
Пример. 4.3. Проанализируем устойчивость системы ФАПЧ из примера 4.2.
Перейдем от D(p) (4.11) к G(iω) (4.15):
U(ω) = a0 – ω2a2 =  , V(ω) =ω(a1 – a3ω2)=
, V(ω) =ω(a1 – a3ω2)=  . (4.20)
. (4.20)
Из совместного решения уравнений U(ω) = 0, V(ω) = 0 получаем:
ω2кр Im=  , ω2кр Re=
, ω2кр Re=  ;
; 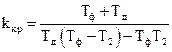 . (4.21)
. (4.21)
Как и следовало ожидать, значение kкр совпало с (4.14).
На рис. 4.7 приведены годографы устойчивых РАС при Тф =0,1 с, Тд = 5 мс, k0 = 200 1/с (46,0 дБ).
График 1 построен при Т2 = 4,7 мс (при Т2 = 4,76 мс 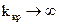 ). Для этого случая kкр = 1,6×104 (84,1 дБ), ωкр Re= 43,6 рад/с, ωкр Im=62,3 рад/с.
). Для этого случая kкр = 1,6×104 (84,1 дБ), ωкр Re= 43,6 рад/с, ωкр Im=62,3 рад/с.
График 2 построен при Т2 = 0. В этом случае kкр = 210 (46,4 дБ), ωкр Re = 43,6 рад/с, ωкр Im=44,7 рад/с. В этом случае запас устойчивости мал (менее 0,5 дБ), и годограф проходит очень близко к критической точке (0,0).
Таким образом, подтвердились сделанные ранее выводы (пример 4.2) о влиянии Т2 форсирующего звена на устойчивость РАС.
Анализируя годографы замкнутых систем, можно установить такое следствие из критерия устойчивости Михайлова.
 Если найти все (j) корни уравнений U(ω) = 0 (ωкр1, ωкр3,…, ωкр2k-1), V(ω) = 0 (ωкр0, ωкр2,…, ωкр2k), то ωкрj должны последовательно перемежаться (ωкр2k-1< ω2k).
Если найти все (j) корни уравнений U(ω) = 0 (ωкр1, ωкр3,…, ωкр2k-1), V(ω) = 0 (ωкр0, ωкр2,…, ωкр2k), то ωкрj должны последовательно перемежаться (ωкр2k-1< ω2k).
С помощью этого следствия можно обойтись без построения годографа. Для этого сначала находят корни (ωкрj) уравнения V(ω) = 0, а затем находят значения U(ωкрj). Если знаки U(ωкрj) с ростом j чередуются, то система будет устойчивой. Если есть хотя бы один участок, на котором не будет чередования знаков – система неустойчива.
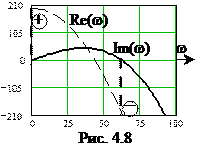
На рис. 4.8 показано применение данного следствия на примере 4.3. Мнимая часть (V(ω)) имеет 2 корня, знаки соответствующих значений U(ω) различны, следовательно, система будет устойчивой.
Критерий Найквиста
На практике более широко применяется критерий Г. Найквиста, разработанный в 1932 г. [10], который позволяет судить об устойчивости замкнутой системы по частотным характеристикам разомкнутой системы.
Пусть разомкнутая РАС устойчива и не содержит идеальных интеграторов.
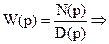
 . (4.22)
. (4.22)
Выражение (4.22) отражает связь ПФ разомкнутой и замкнутой систем.
Поскольку у реальных РАС порядок полинома числителя N(p) не может превышать порядок полинома знаменателя D(p), порядки полиномов D(p) и D(p)+N(p) будут одинаковы.
Проанализируем характеристический вектор
 . (4.23)
. (4.23)
Числитель (4.23) является характеристическим вектором замкнутой системы, а знаменатель – характеристическим вектором разомкнутой системы.
Пусть характеристическое уравнение замкнутой системы имеет m правых корней (n–m – число левых корней), а характеристическое уравнение разомкнутой системы – l правых корней (n–l – число левых корней). Изменение аргумента вектора F(iω) при изменении ω от –∞ до +∞ составит
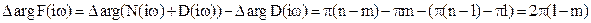 . (4.24)
. (4.24)
Для устойчивой замкнутой системы m=0.
Следовательно при изменении ω от 0 до ∞
 . (4.25)
. (4.25)
Если РАС устойчива в разомкнутом состоянии (l=0), то 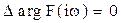 .
.
Таким образом, если разомкнутая и замкнутая системы устойчивы, то изменение аргумента вектора F(iω) равно нулю, следовательно, его годограф не охватывает начало координат. Если годограф F(jω) охватывает начало координат, то система в замкнутом состоянии не устойчива.
От годографа F(iω) удобно перейти к годографу разомкнутой системы W(iω). Если в разомкнутом положении система устойчива, тогда в замкнутом состоянии она также будет устойчива, если годограф Найквиста начинается на действительной полуоси ЧПФ и при изменении ω от 0 до ∞ не охватывает критическую точку (–1, i0).
Если точка (–1, i0) охватывается, то система в замкнутом состоянии будет неустойчива. Если кривая проходит через точку (–1, i0), то система нейтральна (находится на границе устойчивости).
 |
На рис. 4.9 показаны годографы F(iω) (рис. 4.9а) и W(iω) (рис. 4.9б) устойчивых (график 1) и неустойчивых (график 2) в замкнутом состоянии систем.
Если РАС неустойчива в разомкнутом состоянии (l¹0), то для оценки устойчивости системы в замкнутом состоянии существует правило переходов Я. З. Цыпкина: для того, чтобы система, неустойчивая в разомкнутом состоянии, была устойчива в замкнутом состоянии необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов годографа через отрезок вещественной оси слева от критической точки (]–∞, –1[ для W(iω)) была равна l/2 (l – число правых корней разомкнутой системы).
Для годографа W(iω) при изменении ω от 0 до ∞ переход вещественной оси ]–∞, –1[ называется положительным, если он происходит сверху вниз, и отрицательным, если он происходит снизу вверх.
Если РАС содержит v идеальных интеграторов, то начальное значение ФЧХ равно –vp/2, а АЧХ – бесконечности. Для оценки устойчивости таких систем в замкнутом состоянии их дополняют дугой –vp/2 бесконечного радиуса, которая соединяет уходящую в бесконечность линию годографа с положительной вещественной полуосью. Критерий Найквиста в этом случае применяется к результирующему графику.
Если годографы W(iω) пересекают вещественную ось только справа от критической точки (–1, i0), такие РАС называют абсолютно устойчивыми.
Если система терять устойчивость не только при повышении коэффициента усиления, но и при его уменьшении (см. рис. 4.10в), то такая система называется условно устойчивой [1].
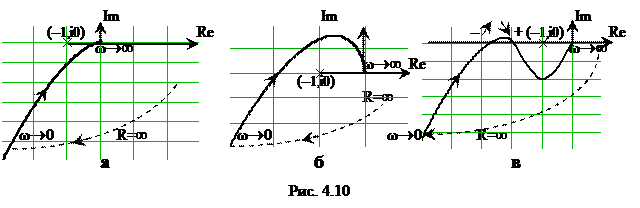 |
На рис. 4.10 приведены годографы W(iω) для систем, которые содержат 1 идеальный интегратор (дуга R=¥ будет иметь размер 1хp/2 (90°)).
На рис. 4.10а построен годограф для системы ФАПЧ из примера 4.2, разомкнутая ЧПФ для которой
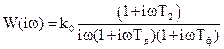 , (4.26)
, (4.26)
а Т2 = 4,7 мс (k0 << kкр). Так как результирующий график не охватывает точку (–1, i0), система в замкнутом состоянии будет абсолютно устойчивой, что подтверждает сделанные ранее выводы.
На рис. 4.10б представлен годограф той же системы при Т2 = 0, k0 = 2 kкр. В этом случае в замкнутом состоянии система будет неустойчивой, так как результирующий график охватывает критическую точку (–1, i0).
На рис. 4.10в показан более сложный случай, когда годограф W(iω) пересекает вещественную полуось ]–∞, –1[ дважды: один переход положительный, второй отрицательный, – значит, разность числа переходов равна нулю (l/2=0). Следовательно, система в замкнутом состоянии будет условно устойчивой.
Дата добавления: 2016-02-20; просмотров: 1947;
