И при произвольном воздействии

Считаем, что x(t)=0, а λ(t) существует только при t ≥ 0 и изменяется медленно. Представим ПФ замкнутой системы по ошибке в виде

. (5.10)

Коэффициенты полученного ряда C_j называются коэффициентами ошибок. Смысл первых коэффициентов ошибок уже известен из результатов п. 5.1 : C₀ = X_пол , C₁ = X_ск , C₂ = X_уск .

Это позволяет определить динамическую ошибку РАС:

. (5.11)

Таким образом, чтобы найти ошибку в установившемся режиме (t → ∞ или p → 0) при произвольных воздействиях и системах, необходимо:

§ определить ПФ замкнутой системы по ошибке (5.4) и представить её в виде отношения двух полиномов;

, (5.12)

§ вычислить коэффициенты ошибок C_j;

§ вычислить производные входного воздействия (t → ∞) : λ′(t), λ″(t), …, λ⁽ⁿ⁾ (t);

§ найти динамическую ошибку по формуле (5.11) и записать установившееся значение ошибки в виде:

. (5.13)

Существуют несколько способов вычисления коэффициентов ошибок:

разложение (5.12) в ряд с учетом того, что p → 0 :

;

деление полинома числителя на полином знаменателя и т. д.

Мы рассмотрим только наиболее простые способы, удобные для вычислений в инженерной практике.

Первый способ. Приравняем (5.10) и (5.12), что в результате дает

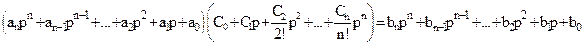. (5.14)

Приравнивая коэффициенты при одинаковых степенях pⁿ, получаем формулы для последовательного вычисления коэффициентов ошибок:

, , , ,

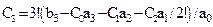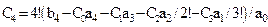, . (5.15)

Второй способ[1, 4]. От (5.14) можно перейти к полиномам M(p) и N(p) ПФ разомкнутой системы (5.3) с порядком астатизма v. Пусть полином числителя M(p) имеет вид .

После подстановки этих условий в (5.14) получим:

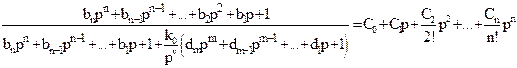. (5.16)

После переноса знаменателя левой части в правую и приведения подобных можно найти связь коэффициентов C_j с коэффициентами полиномов M(p) и N(p), приравнивая коэффициенты при одинаковых степенях pⁿ [1, 4] .

. (5.17)

Операции по (5.17) существенно сложнее, чем по (5.14), но позволяют проводить вычисления по ПФ разомкнутой системы. Приведем несколько готовых результатов из [4] при различных порядках астатизма v.

v = 0. , , .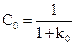

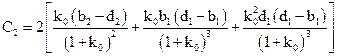v = 1. , , .

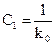v = 2. , , 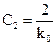. (5.18)

Анализ подтверждает результаты, полученные в п. 5.1: для астатической системы порядка v первые v коэффициентов ошибок равны нулю (C_v-1=0, C_v-2=0,…, C₀=0,), и лишь начиная с C_v, получаются ненулевые коэффициенты.

Пример 5.1. Определим динамическую ошибку РАС ФАПЧ из примера 4.2 при входном воздействии λ(t) = (λ₀+λ₁t+λ₂t²)1(t) при отсутствии возмущения ξ(t).

Запишем ПФ разомкнутой системы (4.9) в виде

. (5.19)

Воспользуемся вторым способом. v = 1, d₁=Т₂, d₀=1, b₂=Т_дТ_ф, b₁=Т_д+Т_ф, b₀=1.

Подставляя в (5.18), получаем:

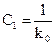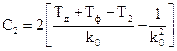, , . (5.20)

Теперь необходимо найти первые две производные λ(t):

λ′(t) = (λ₁+2λ₂t), λ″(t) = 2λ₂. (5.21)

В результате из (5.11) получаем

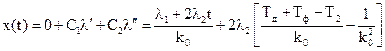, (5.22)

а .

Таким образом, для получения конечной ошибки в установившемся режиме в систему необходимо добавить еще один идеальный интегратор. Увеличение k₀ и Т₂ уменьшает значение ошибки, а повышение Т_д, Т_ф – увеличивает ошибку.

Рассмотрим вычисление коэффициентов C_j первым способом.

Для этого необходимо получить ПФ по ошибке:

K_λx(p) = = 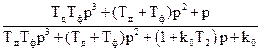. (5.23)

b₃=Т_дТ_ф, b₂=Т_д+Т_ф, b₁=1, b₀=0, а₃=Т_дТ_ф, а₂=Т_д+Т_ф, а₁=1+k₀Т₂, а₀= k₀.

После вычислений по формулам (5.15) получим те же результаты, что получились первым способом в (5.20). Искать C₃ смысла нет, так как производные λ(t), начиная с третьей, равны нулю.

В данном примере второй способ оказался эффективнее.