Анализ устойчивости по логарифмическим характеристикам
От критерия Найквиста можно перейти к анализу устойчивости на основе ЛАЧХ и ЛФЧХ, в том числе асимптотических (диаграмм Боде). Этот метод получил широкое распространение в инженерной практике из-за своей простоты и наглядности. Если выделить модуль и фазу W(iω), а затем перейти к ЛАЧХ и ЛФЧХ, можно сформулировать следующие условия устойчивости.
Для того, чтобы РАС была устойчива в замкнутом состоянии, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов ЛФЧХ прямых ±(2n+1), где n – натуральное число, во всех областях, где ЛАЧХ положительна, была равна l/2, где l – число правых корней характеристического уравнения разомкнутой системы.
Если система устойчива в разомкнутом состоянии (l=0), условие устойчивости существенно упрощается. Рассмотрим точку пересечения годографа W(iω), охватывающего критическую точку (–1, i0), с вещественной полуосью ]–∞, –1[. Соответствующая частота, на которой происходит это пересечение называется критической частотой (fкр или ωкр). ЛФЧХ на критической частоте равна 180° (180°±360°n или p±pn радиан).
Модуль этой точки (–k, i0) будет k>1, а фаза составит 180°. Как известно для усилителя, охваченного отрицательной обратной связью, это соответствует превращению обратной связи в положительную. Так как при этом коэффициент усиления превышает единицу, усилитель самовозбуждается.
Если годограф W(iω) не охватывает критическую точку, то при фазе 180° в точке пересечения с вещественной полуосью ]–∞, –1[ модуль W(iω) k<1, и система будет устойчивой в замкнутом состоянии.
Частота, на которой ЛАЧХ пересекает уровень 0 дБ(АЧХ – уровень единицы), называется частотой среза (fср или ωср).
Очевидно, что для устойчивой РАС должно выполняться условие: ωср > ωкр – частота среза(ЛАЧХ)должна быть больше критической частоты (ЛФЧХ).
Если частота среза ниже критической (ωср < ωкр) – система неустойчива.
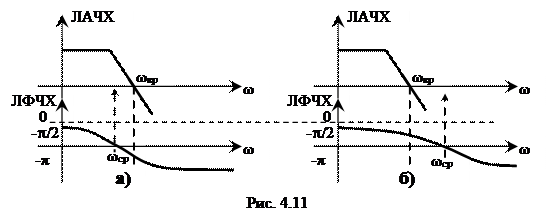 |
На рис. 4.11. показаны ЛАЧХ и ЛФЧХ неустойчивой (рис. 4.11а) и устойчивой систем (рис. 4.11б).
В процессе эксплуатации РАС ее параметры (коэффициенты усиления, постоянные времени и т. п.) из-за изменения внешних условий (колебания напряжения источников питания, старение элементов РАС и т. п.), могут отличаться от расчетных (или номинальных). Если не принять определенных мер, то РАС может стать неустойчивой. Поэтому при проектировании РАС для исключения этого явления необходимо обеспечить запас устойчивости.
Запасы устойчивости определяются на частоте среза (запас устойчивости по фазе jз) и критической частоте (запас устойчивости по усилению Аз).
Запас устойчивости по усилению (4.27) определяет во сколько раз необходимо увеличить коэффициент усиления разомкнутой РАС, чтобы она оказалась на границе устойчивости.
 или
или  . (4.27)
. (4.27)
Запас устойчивости по фазе (4.28) показывает на какое значение ФЧХ (ЛФЧХ) разомкнутой РАС на частоте среза отличается от p±pn (180°±360°n).
 или
или  . (4.28)
. (4.28)
Для нормальной работы РАС обычно требуется запас устойчивости по усилению не менее 2 (6 дБ), а запас по фазе – порядка 40-60°.
Если φ3 ≥ 90˚, то переходный процесс имеет апериодический характер, а при φ3 < 30° получается колебательная ПХ.
 Пример 4.4. Проанализируем устойчивость системы ФАПЧ из примера 4.2.
Пример 4.4. Проанализируем устойчивость системы ФАПЧ из примера 4.2.
Построим ЛАЧХ и ЛФЧХ: выделив модуль и фазу W(iω) из выражения (4.26)
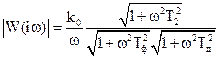 ,
,
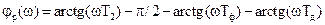 ,
,
перейдем от АЧХ к ЛАЧХ (перевод в дБ по оси L(w) и переход к логарифмическому масштабу по частоте), k0=200 = 46,0 дБ.
Частоты сопряжения, необходимые для постройки асимптотических ЛАЧХ и ЛФЧХ (диаграмм Боде), получаются такие:
wф = 1/Тф = 10 рад/с, wд = 1/Тд = 200 рад/с,
w21 = 1/Т2 = 213 рад/с (при Т2 = 4,7 мс).
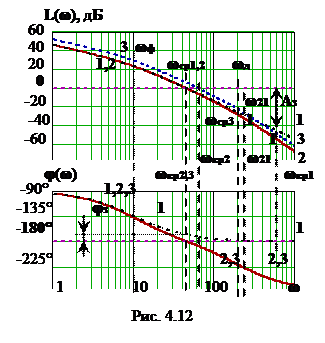
На рис. 4.12 представлены графики ЛАЧХ и ЛФЧХ для трех случаев.
График 1 построен для устойчивой системы (Т2 = 4,7 мс, k0 << kкр, ωср1 » 45 рад/с, ωкр1 » 400 рад/с). Запас устойчивости по усилению составляет более 40 дБ, а запас по фазе – 15°. Запас устойчивости по усилению достаточный, но запас по фазе слишком мал. Следует ожидать, что недостаток запаса по фазе приведет к колебательной форме ПХ со значительным перерегулированием и длительным временем регулирования (установления переходного процесса).
Желательна коррекция.
График 2 построен при Т2 = 0, k0 << kкр = 210 (ωср1 = 43,7 рад/с, ωкр1= 44,7 рад/с). Хотя формально система устойчива (ωср > ωкр), запас устойчивости по усилению и по фазе практически отсутствует, и такая РАС не будет в реальных условиях устойчиво работать, необходимо скорректировать ее характеристики. Для коррекции, как отмечалось в примере 4.2, достаточно увеличить Т2 (например, до 4,7 мс) и (или) снизить k0.
График 3 построен для системы при Т2 = 0, k0 =2 kкр. Получилось, что ωср1 = 61,4 рад/с, ωкр1= 44,7 рад/с Из условий (k0 > kкр) было очевидно, что РАС будет неустойчива, что и подтвердил анализ (ωср < ωкр).
 Пример 4.5. Проанализируем РАС (рис. 4.13) при следующих исходных данных K1=Sд,
Пример 4.5. Проанализируем РАС (рис. 4.13) при следующих исходных данных K1=Sд,  , Т1 = 0,1с; Т2 = 0,01с; Т3 = 0,0001с; Sд = 10.
, Т1 = 0,1с; Т2 = 0,01с; Т3 = 0,0001с; Sд = 10.
Сначала получаем ЧПФ разомкнутой системы:
 .
.
Затем получаем ЛАЧХ и ЛФЧХ:
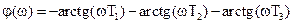 ,
,
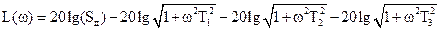 ,
,
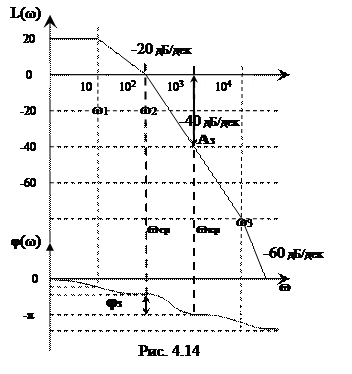 На рис. 4.14 построены асимптотические ЛАЧХ и ЛФЧХ. (w1 = 10 рад/с, w2 = 100 рад/с, w3 = 104 рад/с.)
На рис. 4.14 построены асимптотические ЛАЧХ и ЛФЧХ. (w1 = 10 рад/с, w2 = 100 рад/с, w3 = 104 рад/с.)
Запас устойчивости по усилению равен 40 дБ, запас устойчивости по фазе »60˚. Запасы устойчивости достаточны. Можно ожидать, что переходный процесс будет иметь малоколебательный характер.
4.7. Устойчивость систем с запаздывающими звеньями.
Рассмотрим, как на устойчивость системы влияет введение запаздывающих звеньев (К(р)=е–рτ или К(ω)=е–iωτ). При применении критерия Найквиста, сначала строится годограф системы без запаздывающих звеньев. Затем каждому фазовому углу, соответствующему j-й частоте, добавляется фазовый сдвиг ωjτ: φ(ωj)–ωjτ. Годограф системы со звеньями запаздывания имеет обычно форму спирали.
Проще проводится анализ с помощью ЛАЧХ, ЛФЧХ. Сначала строятся характеристики РАС без запаздывающих звеньев. После этого для учета влияния запаздывания требуется сместить ЛФЧХ на величину запаздывания по фазе.
Из-за изменения запаса по фазе после введения звена с запаздыванием система может перейти в неустойчивое состояние.
Пример 4.6.Проанализируем устойчивость системы ФАПЧ из примера 4.2. с помощью непосредственного вычисления корней характеристического полинома замкнутой системы (4.11). Хотя уравнение до четвертой степени включительно можно решить аналитически, удобнее находить корни с помощью специализированных математических пакетов.
Найдем корни с помощью MathCad. Проще всего это делается с помощью функции polyroots.
При k0=200, Т2 = 4,7 мс получаем такие корни: р1=–200,6; р2,3=–4,7±i44,4. Система устойчива. По виду корней очевидно, что переходный процесс будет иметь колебательный характер.
При k0=200, Т2 = 0 получаем корни: р1=–209,6; р2,3=–0,2±i43,7. Система устойчива, но вещественная часть существенно приблизилась к границе устойчивости. В этом случае усилится колебательность ПХ.
При k0=420, Т2 = 0 система будет неустойчива, так как появляются правые корни: р1=–218,4; р2,3=+4,2±i61,9. Переходный процесс будет иметь колебательный характер с нарастающей амплитудой.
При k0=kкр =210, Т2 = 0 получаем корни: р1=–210; р2,3=0±i44,7. Система находится на колебательной границе устойчивости. В этом случае ПХ будет иметь вид колебаний с постоянной амплитудой.
Полученные ранее выводы об устойчивости РАС (примеры 4.2 – 4.4) подтвердились.
Таким образом, в настоящее время устойчивость системы можно анализировать непосредственным вычислением корней характеристического полинома.
Дата добавления: 2016-02-20; просмотров: 13523;
