Правила структурных преобразований
При анализе сложных схем для получения ПФ системы в целом удобно использовать правила структурных преобразований, которые позволяют упростить схему РАС и расчеты ее характеристик.
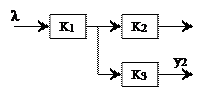
1. Каскадное соединение (рис. 2.7):
 |
Итоговая ПФ каскадного соединения Кå (соответственно Lå(w)) имеет вид:
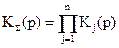 ,
, 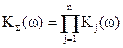 ,
,
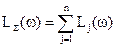 . (2.23)
. (2.23)
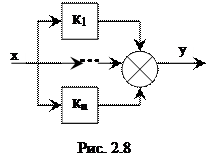
2. Суммирование звеньев (рис. 2.8):
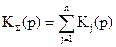 ,
, 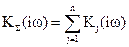 . (2.24)
. (2.24)
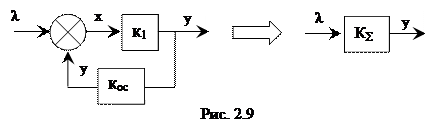
3. Звено с обратной связью (ОС) (рис. 2.9):
После преобразований для звена с ОС получаем
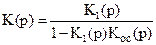 (для положительной ОС) и
(для положительной ОС) и
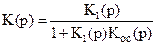 (для отрицательной ОС) . (2.25)
(для отрицательной ОС) . (2.25)
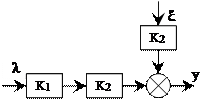
4. Перенесение сумматора.
Рассмотрим перенос сумматора влево и вправо от исходной точки включения и дополним схему таким образом, чтобы ПФ системы по входному воздействию (Kλy(p)=K1(p)K2(p)) и возмущению (Kξy(p)=K2(p)) не изменилась.
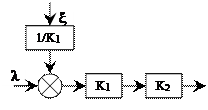
| 
| 
|
Таким образом, при переносе сумматора влево для сохранения тех же ПФ РАС необходимо добавить в цепь воздействия или возмущения, входящего в сумматор, звено с ПФ 1/K1, а при переносе вправо – звено с ПФ K2.
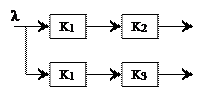
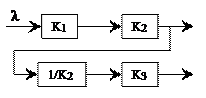
5. Перенесение точки разветвления.
Рассмотрим перенос точки разветвления влево и вправо от исходной точки включения и дополним схему таким образом, чтобы ПФ системы по входному воздействию (Kλy1(p)=K1(p)K2(p) и Kλy2(p)=K1(p)K3(p)) не изменилась.
|
|
|
Таким образом, при переносе точки разветвления влево для сохранения тех же ПФ РАС необходимо добавить в цепь разветвления звено с ПФ K1, а при переносе вправо – звено с ПФ 1/K2.
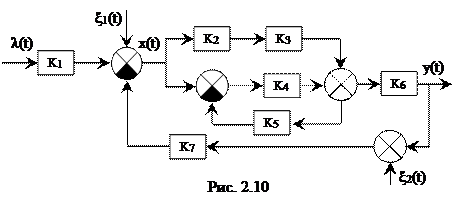 |
Пример 2.1. Упростить схему, показанную на рис. 2.10.
Выделим соединения, допускающие упрощение. Звенья с K2 и K3 соединены каскадно, что позволяет заменить их одним звеном с K23 = K2×K3.
Звенья с K4 и K5 имеют обратную связь, что позволяет заменить их одним звеном с K45 = K4/(1+ K4×K5). ПФ полученных звеньев следует сложить на сумматоре перед звеном с K6 , а затем полученное звено (его ПФ K25 = K23 + K45) каскадно соединяется с с K6, что в результате дает
 K26 = [K2×K3 + K4/(1+ K4 ×K5)]×K6 = K2×K3×K6 + K4×K6/(1+ K4 ×K5) . (2.26)
K26 = [K2×K3 + K4/(1+ K4 ×K5)]×K6 = K2×K3×K6 + K4×K6/(1+ K4 ×K5) . (2.26)
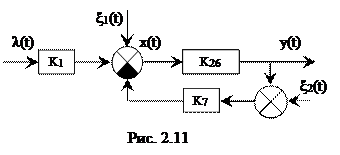
В результате получаем схему, показанную на рис. 2.11
Эту схему можно упрощать и дальше: перенести сумматор с ξ2(t) к точке приложения ξ1(t), преобразовать обратную связь звеньев с K26 и K7, но можно и по этой схеме определить ПФ выходного процесса и ПФ ошибки по входному воздействию λ(t) и возмущениям ξ1(t), ξ2(t) с помощью формул следующего параграфа.
Дата добавления: 2016-02-20; просмотров: 1193;