Розділ 4. Детерміновано-статистичні методи
Розпізнавання образів
Метод еталонів Турбовича
Об’єднати переваги як детермінованого, так і статистичного підходів до розпізнання образів та обійти їх недоліки – така задача розв’язується у рамках детерміновано-статистичного підходу, наприклад, у праці [], де запропоновано будувати класифікатор у два етапи. На першому етапі будується найбільш просте детерміноване вирішальне правило, яке забезпечує безпомилкове розпізнавання реалізацій навчальної матриці. Для мінімізації кількості помилок і прогнозу їх величин при розпізнаванні на другому етапі здійснюється непараметрична статистична корекція вирішального правила. Для такої корекції використовують два одномірних параметри, оцінку яких можна отримати за класифікованою навчальною матрицею. Це максимально-можливий викид реалізацій за “свою” еталонну оболонку та максимально-можливе проникнення у глибину еталонних оболонок реалізацій “чужих” образів.
Метод еталонного опису
Подальшим розвитком методу еталонів став метод еталонного опису [5], в якому з метою зменшення кількості еталонів, а отже і спрощення мінімізації покриття класу, акцент зроблено на відбір ефективних ознак розпізнавання шляхом оцінки їх корисності.
Модельність як методу еталонів, так і методу еталонного опису полягає в ігноруванні загального випадку перетину класів і у відсутності оптимізації процесу навчання за прямим КФЕ, що знижує їх практичну цінність.
4.3.Узагальнена математична модель розпізнавання образів
Розглянемо математичну модель класичної задачі автоматичної класифікації на рівні системного аналізу. Така модель повинна включати як обов'язкову складову частину вхідний математичний опис, який подамо у вигляді теоретико-множинної структури:
DВ=<G, T, 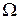 , Z, V, Y; П, Ф>, (4.3.1)
, Z, V, Y; П, Ф>, (4.3.1)
де G -простір вхіднихсигналів (факторів), які діють на систему розпізнавання; T - множина моментів часу зняття інформації;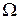 - простір ознак розпізнавання;Z– простір можливих станів системи розпізнавання;V–множина вирішальних правил; Y-множина сигналів, які знімаються з виходу блоку первинного оброблення інформації; П: G
- простір ознак розпізнавання;Z– простір можливих станів системи розпізнавання;V–множина вирішальних правил; Y-множина сигналів, які знімаються з виходу блоку первинного оброблення інформації; П: G 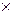 T
T 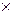
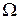
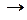 Z-оператор переходів, що відбиває механізм зміни станів системи розпізнавання під дією внутрішніх і зовнішніх збурень; Ф: G
Z-оператор переходів, що відбиває механізм зміни станів системи розпізнавання під дією внутрішніх і зовнішніх збурень; Ф: G 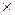 T
T 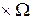
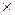 Z
Z 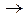 Y - оператор формування вибіркової множини Y на вході системи розпізнавання.
Y - оператор формування вибіркової множини Y на вході системи розпізнавання.
Як універсум випробувань Wбудемо розглядати декартовий добуток наведених в (4.3.1) множин: W = G 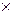 T
T 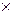
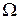
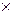 Z
Z 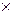 V.
V.
Для чіткого (детермінованого) розбиття 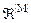 потужності M, оператор його побудови задає бієктивне відображення
потужності M, оператор його побудови задає бієктивне відображення 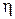 :Y
:Y 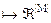 . Апріорно оператором n:Y®L|M| для заданого алфавіту
. Апріорно оператором n:Y®L|M| для заданого алфавіту 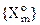 будується покриття L|M|, що корегується апостеріорно оператором æ
будується покриття L|M|, що корегується апостеріорно оператором æ 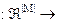 L|M|. Перевірка гіпотези про належність реалізацій образу здійснюється оператором класифікації
L|M|. Перевірка гіпотези про належність реалізацій образу здійснюється оператором класифікації 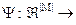 I|M+1|, де I|M+1| - множина допустимих гіпотез. При цьому гіпотеза
I|M+1|, де I|M+1| - множина допустимих гіпотез. При цьому гіпотеза 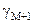
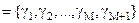 означає відмову від класифікації. У загальному випадку математичну модель будь-якої системи розпізнавання подамо у вигляді діаграми відображень відповідних множин []:
означає відмову від класифікації. У загальному випадку математичну модель будь-якої системи розпізнавання подамо у вигляді діаграми відображень відповідних множин []:
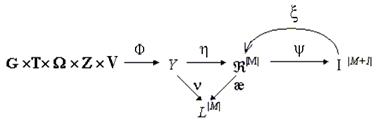
(4.3.2)
У діаграмі (4.3.2) оператор зворотного зв’язку x корегує геометричні параметри розбиття 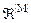 з метою покращення точнісних характеристик класифікатора. Саме спосіб реалізації оператора xпороджуєрізні методи та підходи до розв’язання проблеми високоефективного навчання СК.
з метою покращення точнісних характеристик класифікатора. Саме спосіб реалізації оператора xпороджуєрізні методи та підходи до розв’язання проблеми високоефективного навчання СК.
Дата добавления: 2016-02-20; просмотров: 705;
