Структура комбінаторного алгоритму

У структурі кожного з алгоритмів МГУА можна виділити три основних блоки:

1. Перетворення початкових даних відповідно до обраної системи опорних функцій, у якій шукається модель.

2. Генерування повної або неповної множини часткових моделей, що ускладнюються, в обраному образі.

3. обчислення значень деякого критерію селекції, що має властивості зовнішнього доповнення і послідовного добору часткових моделей, кращих за цим критерієм.

Блок формування базису.

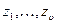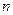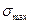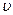Якщо задані виміри деяких вхідних перемінних об’єкта, що моделюється, і максимальний ступінь полінома, то число доданків у повному поліномі ступеня від перемінних визначається однозначно:

.

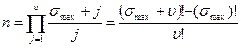Сам повний поліном записується в наступному загальному вигляді:

,

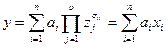де кожен узагальнений «лінійний» аргумент 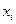є нелінійною функцією початкових перемінних :

.

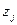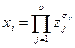Отже, 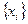‑ базисний набір опорних функцій.

Описана процедура дозволяє сформувати матрицю виміру узагальнених аргументів 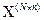, де 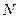‑ число точок вимірів.

Ці точки розділені на три послідовності: навчальну (А) довжиною 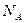, перевірочну (В) довжиною 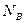й екзаменаційну (С) довжиною 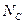. Причому

.

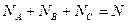Блок перебору часткових моделей.

Основні операції:

- формування структури чергової часткової моделі;

- формування відповідної нормальної системи рівнянь;

- вирішення отриманої системи (оцінка коефіцієнтів моделі).

Формування структур часткової моделі формалізується за допомогою структурного вектора 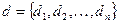: якщо елемент 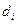цього вектора приймає значення 1, то відповідний 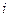-й аргумент включається в часткову модель, якщо 0 – не включається.

Використовується схема зміни двоїстого вектора за принципом роботи двоїстого лічильника, в останній розряд якого додається одиниця.

Формування нормальної системи рівнянь, що відповідає черговому структурному вектору, можна виконати формально: зі стовпців повної матриці 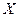, зазначених одиничними елементами 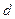, складається часткова матриця 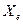, а потім обчислюються елементи .

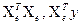В комбінаторному алгоритмі досить один раз обчислити матрицю повної нормальної системи, що містить елементи всіх часткових нормальних систем:

, .

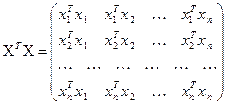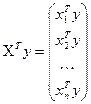Для одержання будь-якої часткової нормальної системи досить взяти елементи матриці 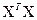, що знаходяться на перетині рядків і стовпців, зазначених одиницями вектора 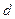, а також відповідні елементи вектора .

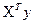Для вирішення кожної нормальної системи 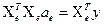, тобто для обчислення оцінок коефіцієнтів часткової моделі, можна застосовувати будь-які процедури розв’язання систем алгебраїчних рівнянь.

Блок добору за критеріями.

Критерій незміщеності:

,

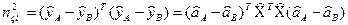де 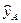, 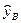‑ оцінки вихідної величини, отримані за коефіцієнтами 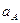, 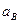; 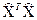‑ сума матриць 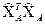і .

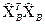Критерій регулярності:

,

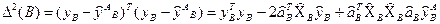де 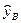‑ початковий вектор вимірів вихідної величини на послідовності В; 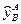‑ оцінки виходу на В по моделі .

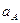На послідовності С

,

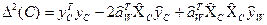де 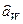‑ оцінки коефіцієнтів часткових моделей, відібраних по 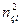і 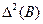після перерахування на об’єднаній послідовності .

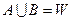Селекція моделей, як правило, виконується в процесі перебору. Для цього запам’ятовується значення критерію для заданої свободи вибору 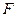перших моделей, а потім величина кожної наступної моделі порівнюється з кращим з 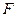значень.

В алгоритмах МГУА звичайно виконується ще один етап обчислень – оцінка якості відібраних кращих моделей .

Помилку МНК, обумовлену після перерахування коефіцієнтів на 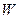, також можна виразити через нормальні матриці

,

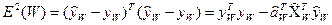де виконується рівність

.

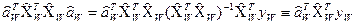Селекція продовжується доти, поки не досягається мінімум критерію незміщеності. Потім відбирається найбільш регулярна модель.

Нечіткий МГУА

Постановка задачі

Задано множину вхідних даних 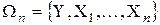, , 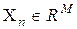де 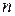‑ кількість змінних, а 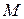‑ кількість точок спостереження. Необхідно за допомогою нечіткого методу групового урахування аргументів синтезувати рівняння регресії 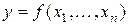, адекватне вихідній множині даних, причому отримана модель повинна бути найменшої складності.

Для прикладу, для обчислення інфляційних процесів були узяті наступні макроекономічні показники на період із січня 1995 року по лютий 1997 року:

- індекс споживчих цін (ІСЦ);

- індекс оптових цін на промислову продукцію;

- випуск промислової продукції;

- роздрібний товарообіг;

- кредитні внески в економіку;

- середньозважений курс долара;

- грошовий доход на душу населення;

- грошовий агрегат М0;

- грошовий агрегат М2;

- середньомісячна заробітна плата;

- ставка НБУ;

- кредиторська заборгованість між підприємствами;

- зміни обсягів валового сукупного продукту.

У результаті виконання роботи необхідно побудувати адекватну модель, що вивчає залежність ІСЦ від інших макроекономічних показників, що має найменшу складність і використовується для прогнозування інфляційних процесів.

Побудова часткової моделі нечіткого МГУА (НМГУА)

Для побудови часткової моделі НМГУА використовувалася лінійна інтервальна регресійна модель, що задається таким чином:

,

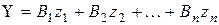де 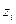‑ деякі відомі перемінні, 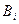‑ інтервали, які можна задати трикутними нечіткими числами і записати таким чином у вигляді центра 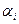і ширини :

.

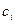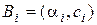Виходячи з цього, 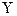можна розрахувати так:

.

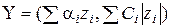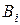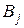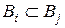Відношення вкладеності двох інтервалів і ( ) можна задати наступними нерівностями: .

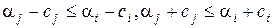У нашому випадку зміні 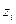зв’язані зі змінними 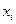і 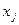дл відповідної часткової моделі НМГУА так:

, , , , …, , .

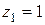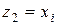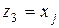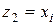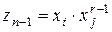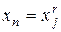Розглянемо метод оцінювання лінійної інтервальної регресійної моделі. Нехай є 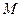спостережень 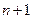перемінної, причому 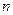з них – незалежні величини, ( 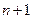)-а залежить від інших, і цю залежність 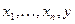ми намагаємося визначити. При цьому 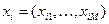і 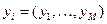‑ вхідні і вихідні вектори точок спостереження. Тоді оціночна лінійна інтервальна модель для часткової моделі НМГУА має вигляд:

.

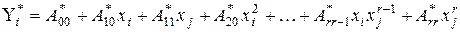Побудова робиться з урахуванням наступних вимог:

1.Задані значення 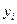, що спостерігаються, включаються в оціночний інтервал .

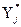2.Ширина оціночного інтервалу повинна бути мінімальною.

Ці вимоги можна звести до задачі лінійного програмування в наступному вигляді (для 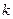-тої точки спостереження):

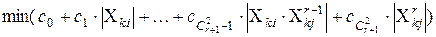; (4.1)

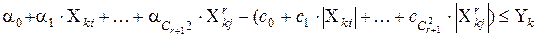; (4.2)

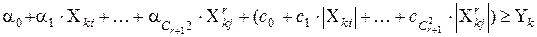; (4.3)

.

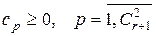Виходячи з цього, при відомих значення перемінних 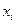і величини 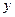, отриманих у результаті 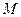вимірів, мо приходимо до задачі пошуку коефіцієнтів моделі (для всіх точок спостереження) у такому вигляді:

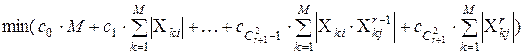; (4.4)

при обмеженнях

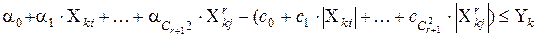; (4.5)

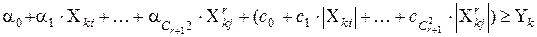; (4.6)

,

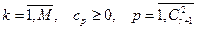де 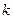‑ номер виміру, дані з яких використовуються.

Завдання полягає у тому, щоб мінімізувати область зміни вихідних значень 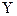за рахунок відшукання таких значень ширини інтервалів – шуканих коефіцієнтів 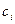і таких значень центрів інтервалів 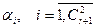, які забезпечували б мінімальне розсіювання величини 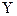одночасно з виконанням умови, що всі вимірювані значення шуканої величини знаходяться в цьому інтервалі. Ця задача є задачею лінійного програмування. Для її рішення перейдемо до двоїстої задачі.

Вирішивши двоїсту задачу симплекс-методом і одержавши оптимальні значення двоїстих змінних, ми зможемо знайти й оптимальні значення шуканих змінних 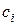і 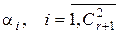, а разом з цим і визначити шукану модель математичної залежності.

Опис ряду селекції

Щоб одержати моделі другого ряду необхідно задати опорну функцію, аргументами якої є функції-моделі, отримані у попередньому ряді.

У нашому випадку опорна функція задавалася також поліномом другого ( 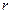-того) ступеня від двох змінних, тобто 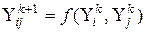, де 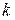‑ номер ряду.

У кожному ряді після генерації всіх можливих моделей за комплексним критерієм у площині критеріїв відбиралися 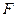кращих моделей, що беруть участь у подальшій генерації. Критерієм зупинки процесу генерації є близькість середнього критерію моделей на двох сусідніх рядах роботи методу, тобто:

.

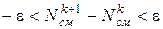При генерації моделей може виникнути явище индуцита, що зв’язане з тим, що після ряду ітерацій 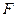моделей 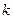-го ряду стануть майже нерозрізнені між собою. Для боротьби з цим явищем вид опорної функції не змінюють, а замість одного з аргументів беруть модель попереднього ряду, тобто .

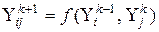Приклад отриманих результатів виконаних експериментів для заданої задачі про макроекономічні показники.

Результати структурної ідентифікації на вікні прогнозування розміром у 15 точок, з яких 10 було виділено на навчальну й 5 – на перевірочну вибірку. При ідентифікації на наступний етап синтезу передавалося 10 кращих моделей поточного етапу.

Використовуваний частковий опис:

.

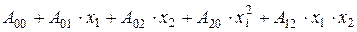Величина СКП: 0,7119462.

1.