Перший і другий принципи адитивності інформації.
Перший принцип адитивності інформації дозволяє в рамках синтаксичного підходу оцінювати цінність інформації через її кількісні характеристики.
Другий принцип адитивності інформації дозволяє визначити робочу область значень інформаційного КФЕ, яка задовольняє вимогам: чим більше кількість інформації про образи, що розпізнаються, тим більша достовірність рішень, що приймаються.
Принцип апріорної недостатності обґрунтування гіпотез (принцип Бернуллі-Лапласа) . Для оцінки ефективності функціонування СК, що навчається, апріорна інформація є неповною, тому, згідно з принципом Бернуллі-Лапласа, виправдано прийняття рівноймовірних гіпотез. При цьому гарантується, що покращення умов функціонування системи не знизить її функціональну ефективність, а навпаки підвищить.
Принцип “найближчого сусіди” обумовлює необхідність побудови оптимальних роздільних гіперповерхонь між найближчими класами розпізнавання.
Принцип рандомізації вхідних даних. Цей принцип дозволяє разом з детермінованими характеристиками функціонального стану СПР розглядати випадкові реалізації образів розпізнавання, що дає змогу оцінювати точнісні характеристики процесу навчання і обчислювати інформаційну спроможність системи.
Основні концептуальні положення ІЕІТ можна сформулювати так:
· метод ґрунтується на прямій оцінці інформаційної спроможності системи розпізнавання, що навчається;
· прийняття рішень здійснюється в рамках детерміновано-статистичного підходу шляхом побудови відносно простого детермінованого класифікатора, статистична корекція якого здійснюється в процесі навчання з метою підвищення достовірності рішень, що приймаються на екзамені;
· метод ґрунтується на застосуванні гіпотез як чіткої, так і нечіткої компактності реалізацій образу, тобто є працездатним за умови перетину класів розпізнавання; що має місце в практичних задачах контролю та керування;
· метод є об’єктно-структурованим, що дозволяє його розвивати для вирішення проблеми інформаційного синтезу широкого класу систем розпізнавання з успадкуванням властивостей структурованих об’єктів вищого ієрархічного рівня і довизначенням їх методів;
· метод базується на вибірковому підході математичної статистики і орієнтований на застосування прийнятних з практичних міркувань мінімальних обсягів репрезентативних навчальних вибірок;
· метод є універсальним для проектування здатної навчатися системи розпізнавання будь-якої природи і дозволяє вирішувати як загальну, так і часткові задачі її інформаційного синтезу.
Основна ідея ІЕІТполягає в оптимізації структурованих просторово-часових параметрів функціонування СПР шляхом трансформації в процесі навчання відношення схожості на нечіткому розбитті простору ознак розпізнавання на класи у відношення еквівалентності. При цьому оптимізація параметрів функціонування здійснюється за ієрархічною ітераційною процедурою пошуку глобального максимуму інформаційного критерію функціональної ефективності навчання системи в робочій області визначення його функції. Побудова безпомилкового за навчальною матрицею класифікатора, згідно з принципами дуальності оптимального керування, редукції, і максимізації інформації при прийнятті рішень, у дискретному субпарацептуальному просторі ознак розпізнавання на кожному кроці навчання здійснюється шляхом цілеспрямованої трансформації вихідного нечіткого розподілу реалізацій образу з метою його вписування в оптимальний контейнер класу розпізнавання, що відновлюється в радіальному базисі. При цьому відновлення контейнерів в радіальному базисі в задачах контролю та керування, де розподіли реалізацій образу є уніномодальними, є природним.
Таким чином, підвищення ефективності машинного навчання системи розпізнавання за умови нечіткої компактності реалізацій образу досягається шляхом цілеспрямованої зміни значень ознак розпізнавання у рамках ІЕІТ, що дозволяє трансформувати апріорне нечітке розбиття простору ознак на класи розпізнавання в чітке з метою побудови безпомилкових за навчальною матрицею вирішальних правил.
Розглянемо бінарний простір ознак розпізнавання WБ, який є підмножиною простору Хеммінга з потужністю Card WБ = 2N, де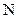 
- число ознак розпізнавання (рецепторів). При класифікаційному аналізі і-та ознака розглядається як випадкова величина, значення якої утворюють на генеральній сукупності повторну вибірку 
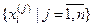обсягу n.
Детерміновано-статистичний підхід до моделювання систем вимагає завдання систем нормованих (експлуатаційних) і контрольних допусків на ознаки розпізнавання. Нехай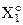 
- базовий клас, який характеризує максимальну функціональну ефективність системи розпізнавання, тобто є найбільш бажаним для ОПР.
Визначення 4.4.1. Нормованим називається поле допусків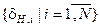 
, в якому значення і–ої ознаки знаходиться з імовірністю рі=1 або pi=0, за умови, що функціональний стан системи розпізнавання образів відноситься до базового класу 
.
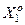Визначення 4.4.2. Контрольним називається поле допусків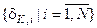 
, в якому значення і-ї ознаки знаходиться з імовірністю 0< рі<1за умови, що функціональний стан СПР відноситься до базового класу 
.
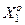В ІЕІТ контрольні допуски на ознаки розпізнавання вводяться з метою рандомізації процесу прийняття рішень, оскільки для повного дослідження процесу керування необхідно використовувати як детерміновані, так і статистичні характеристики. Зрозуміло, що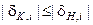 
і базова система контрольних допусків є сталою для всього алфавіту класів розпізнавання.
Визначення 4.4.3. Реалізацією образу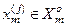 
називається випадковий структурований двійковий вектор
, 
,
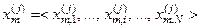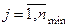де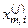 
- і-та координата вектора, яка приймає одиничне значення, якщо значення і-ої ознаки знаходиться в полі допусків 
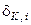, і нульове значення, якщо не знаходиться; 
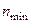- мінімальна кількість випробувань, яка забезпечує репрезентативність навчальної вибірки.
При обґрунтуванні гіпотези компактності (чіткої, або нечіткої) за геометричний центр класу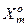 
приймається вершина двійкового еталонного вектора хm.
Процес прийняття рішень складається з двох етапів: навчання (самонавчання) і безпосереднього розпізнавання або екзамену.
Визначення 4.4.4. Середньою максимальною асимптотичною (верхньою граничною) повною достовірністю системи розпізнавання, що навчається, називається ймовірність
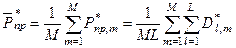, (4.4.3)
де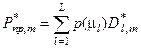 
– асимптотична повна достовірність розпізнавання реалізацій класу 
; 
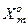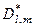- екстремальне асимптотичне значення l-ої достовірності розпізнавання реалізацій класу 
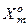, яка визначає максимум 
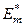інформаційного КФЕ процесу навчання; L – кількість статистичних гіпотез. Тут 
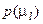– безумовна ймовірність прийняття статистичної гіпотези, яка за принципом Бернуллі-Лапласа в ІЕІТ дорівнює 
.
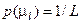При оптимізації процесу навчання за ІЕІТ роздільні гіперповерхні класів розпізнавання відновлюються у вигляді контейнерів, які складаються із правильних геометричних фігур або їх об’єднання, що зменшує обчислювальну трудомісткість алгоритму навчання. Особливо це ефективно при побудові контейнерів у радіальному базисі.
Ефективність функціонування системи розпізнавання залежить від її параметрів функціонування.
| |
Визначення 4.4.6.Як критерій оптимізації процесу навчання в рамках ІЕІТ застосовується будь-який статистичний логарифмічний інформаційний КФЕ, який є природною мірою різноманітності класів розпізнавання і одночасно функціоналом точнісних характеристик нечіткого регулятора.
Важливим параметром функціонування системи розпізнавання є рівень селекції координат еталонного двійкового вектора, вершина якого визначає геометричний центр класу розпізнавання.
Визначення 4.4.7. Рівнем селекції координат еталонного двійкового вектора називається рівень квантування дискрет полігону емпіричних частот попадання значень ознак розпізнавання у свої поля контрольних допусків.
Полігон будується для кожного класу так: по осі абсцис відкладаються ранги ознак розпізнавання, які відповідають номерам ознак у векторі-кортежі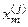 
, а по осі ординат – відносні частоти wm,i =ni /n, де ni – кількість випробувань, при яких значення і-ї ознаки знаходиться в своєму полі контрольних допусків. За умовчанням приймається рівень селекції rm= 0,5..
Визначення 4.4.8.Відносним коефіцієнтом нечіткої компактності реалізацій класу 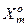для гіперсферичного класифікатора називається відношення
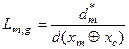, (4.4.3)
де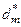 
– оптимальний в інформаційному розумінні радіус контейнера класу 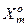, який забезпечує максимальну різноманітність між найближчими сусідніми класами розпізнавання; 
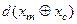– кодова відстань між центрами класу 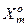і його найближчим сусідом – класом 
.
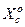У бінарному просторі формою оптимального контейнера є гіперпаралелепіпед. З метою узагальнення та зручності побудови такого контейнера допустимо існування “псевдогіперсфери”, яка описує гіперпаралелепіпед, тобто містить усі його вершини. Це дозволяє далі розглядати такі параметри оптимізації контейнера в радіальному базисі, як еталонний вектор, наприклад,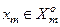 
, вершина якого визначає геометричний центр контейнера 
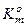, і радіус псевдосферичного контейнера, який визначається у просторі Хеммінга за формулою:
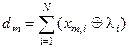, (4.4.5)
де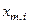 
- i-та координата еталонного вектора 
; 
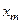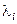- i-та координата деякого вектора 
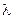, вершина якого належить контейнеру 
.
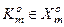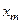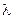Надалі, з метою спрощення, кодова відстань (4.4.5) між векторами і буде позначатися так само у вигляді 
.
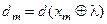У загальному випадку при прийнятті гіпотези нечіткої компактності реалізацій образу покриття L|M| =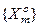 
не є чіткою фактор-множиною 
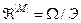, де Э - відношення еквівалентності. Якщо для нечіткого простору ознак 
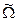існує нечітке покриття 
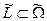і визначено міру 
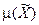як відношення діаметрів нечітких множин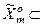 
, 
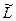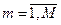, і 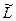, то покриття 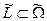є нечітким розбиттям 
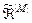, яке відповідає умовам:
1) 
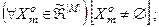
2) 
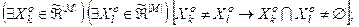
3) 
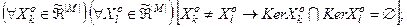4) 
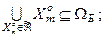
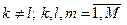. (4.4.5)
В ІЕІТ відновлення оптимального контейнера в радіальному базисі, наприклад, 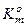здійснюється шляхом його цілеспрямованої послідовної трансформації в гіперсферичний габарит, радіус 
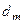якого збільшується на кожному кроці навчання за рекурентною процедурою:
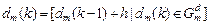, (4.4.6)
де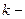 
змінна числа збільшень радіуса контейнера ; 
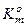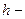крок збільшення радіуса; 
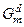– область допустимих значень радіуса 
.
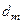Нехай класи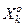 
і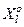 
є “найближчими сусідами”, тобто мають серед усіх класів найменшу міжцентрову відстань 
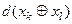, де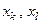 
- еталонні вектори відповідних класів. Тоді за ІЕІТз метою запобігання “поглинання” одним класом ядра іншого класу умови (4.4.5) доповнюються таким предикатним виразом:
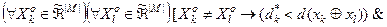
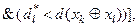(4.4.7)
де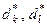 
- оптимальні радіуси контейнерів 
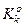і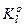 
відповідно.
Алгоритм навчання за ІЕІТ полягає в реалізації багатоцикличної ітераційної процедури оптимізації структурованих просторово-часових параметрів функціонування СПР шляхом пошуку глобального максимуму усередненого за алфавітом 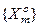значення КФЕ навчання.
Нехай вектор параметрів функціонування системи розпізнавання у загальному випадку має таку структуру:
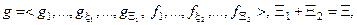(4.4.7)
де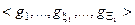 
– генотипні параметри функціонування, які впливають на параметри розподілу реалізацій образу; 
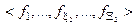– фенотипні параметри функціонування, які прямо впливають на геометрію контейнера класу розпізнавання.
При цьому відомі обмеження на відповідні параметри функціонування:
; 
.
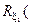
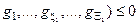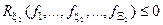За методологією об’єктно-орієнтованого проектування подамо тестовий алгоритм навчання в рамках ІЕІТ для загального випадку (М>2) як ієрархічну ітераційну процедуру оптимізації структурованих просторово-часових параметрів (4.4.7) функціонування системи розпізнавання:
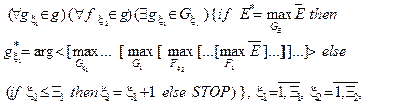(4.4.8)
де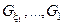 
- області допустимих значень відповідних генотипних параметрів навчання; 
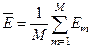– усереднене значення КФЕ навчання системи розпізнавання; 
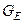– область значень функції інформаційного КФЕ навчання; 
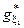- оптимальне значення параметра навчання, яке визначається у зовнішньому циклі ітераційної процедури оптимізації; 
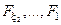– області допустимих значень відповідних фенотипних параметрів навчання. Тут 
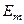– інформаційний КФЕ навчання СК розпізнавати реалізації класу .
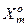Глибина циклів оптимізації визначається кількістю параметрів навчання у структурі (4.4.7). При цьому внутрішні цикли оптимізують фенотипні параметри навчання, які безпосередньо впливають на геометричну форму контейнерів класів розпізнавання. Такими параметрами, наприклад, для гіперсферичних контейнерів класів є їх радіуси. До генотипних у ІЕІТ відносяться параметри навчання, які прямо впливають на розподіл реалізацій класу (наприклад, контрольні допуски на ознаки розпізнавання, рівні селекції координат еталонних двійкових векторів, параметри оптимізації словника ознак, плану навчання, параметри впливу середовища та інше). Послідовна оптимізація кожного із цих параметрів дозволяє збільшувати значення максимуму КФЕ навчання, що підвищує повну асимптотичну достовірність класифікатора на екзамені. Обов’язковою процедурою алгоритму навчання за ІЕІТ є оптимізація контрольних допусків, величина яких безпосередньо впливає на значення відповідних ознак розпізнавання, а так само і на параметри розподілу реалізацій образу.
При компараторному розпізнаванні (М=2), яке відбувається шляхом порівняння образу, що розпізнається, з еталонним образом, і має місце, наприклад, в задачах ідентифікації кадрів, самонаведенні літальних апаратів, класифікаційному самонастроюванні та інше, ітераційний алгоритм навчання за ІЕІТ має такий структурований вигляд:
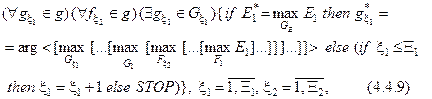
де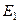 
– інформаційний КФЕ навчання системи розпізнавати реалізації еталонного класу 
.
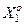Таким чином, за умови обґрунтування гіпотези компактності (чіткої або нечіткої), основна ідея навчання за ІЕІТ полягає в послідовній нормалізації вхідного математичного опису системи розпізнавання шляхом цілеспрямованої трансформації апріорних габаритів розкиду реалізацій образів з метою максимального їх захоплення контейнерами відповідних класів, що відбудовуються в радіальному базисі в процесі навчання. Оптимальні контейнери за ІЕІТ забезпечують максимальну різноманітність між сусідніми класами, міра якої дорівнює максимуму інформаційного КФЕ навчання в робочій області визначення його функції. Оптимальні геометричні параметри контейнерів, отримані в процесі навчання, дозволяють на екзамені приймати рішення за відносно простим детермінованим вирішальним правилом, що важливо при реалізації алгоритмів прийняття рішень в реальному темпі часу. При цьому повна достовірність класифікатора наближається до максимальної асимптотичної, яка визначається ефективністю процесу навчання. Досягнення на екзамені асимптотичної достовірності розпізнавання можливо за умови забезпечення однакових характеристик статистичної стійкості та статистичної однорідності навчальної та екзаменаційної матриць.
5. МЕТОД ГРУПОВОГО ВРАХУВАННЯ АРГУМЕНТІВ (МГВА)
Значний внесок в розвиток ряду перспективних напрямків досліджень в сфері штучного інтелекту зробив академік НАНУ О.Г. Івахненко та його учні, які ще в 70- роки розробили нові алгоритми навчання та самонавчання розпізнаючих систем, що знайшли відображення в численних монографіях.
Особливо слід відзначити вклад О.Г.Івахненка в створення принципово нового методу індуктивного моделювання складних систем – МГУА, який уже понад 30 років з успіхом використовується не тільки в Україні, але й у провідних зарубіжних країнах (США, Японія, Німеччина) для розробки моделей складних інтелектуальних систем.
Дата добавления: 2016-02-20; просмотров: 883;