Багаторядні поліноміальні алгоритми МГУА

Багаторядні алгоритми МГУА застосовуються для рішення некоректних чи недовизначених задач моделювання, тобто у випадку, коли число точок у таблиці дослідних даних менше числа аргументів, що входять у синтезовану модель. Методи регресійного аналізу в цьому випадку незастосовні, тому що не дають можливості побудови єдиної моделі, адекватної процесу за межами інтервалу інтерполяції. Застосування багаторядних алгоритмів МГУА не обмежується зазначеною областю некоректних (недовизначених) задач. Вони успішно застосовуються й у випадках, коли вихідних досить для застосування однорядних МГУА, однак при цьому багаторядні часто виявляються кращими.

Опис алгоритму

Перша ітерація.

Крок 1. З множини виходів 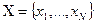вибираються пари аргументів 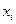, 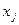і складаються часткові описи виду

,

, ,

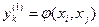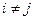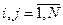при цьому використовують часткові описи квадратичного типу:

.

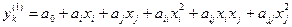Число часткових описів 1-го ряду дорівнює .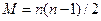

Крок 2. Використовуючи метод найменших квадратів (МНК) для кожного опису знаходяться по навчальній вибірці оцінки невідомих коефіцієнтів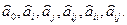

Крок 3. За критерієм мінімуму 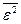на перевірочній послідовності відбирається 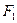кращих моделей, тобто реалізують процедуру селекції. Величина 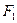називається свободою вибору, при цьому 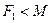. Виходи цих моделей служать аргументами-входами для конструювання моделей другого ряду.

Крок 4. Знаходиться .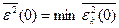

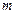-а ітерація.

Крок 1. Конструюються часткові описи виду:

,

.

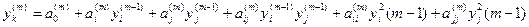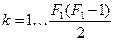Крок 2. Для кожного опису, використовуючи МНК, знаходяться відповідні оцінки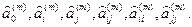

Крок 3. На перевірочній послідовності знаходиться для кожного часткового опису величина критерію

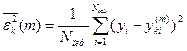
де 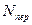‑ обсяг перевірочної вибірки.

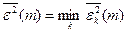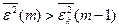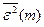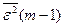Крок 4 Знаходиться . Перевіряється умова , де , ‑ величини критерію точності для найкращих моделей 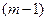-го і 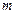-го ряду селекції відповідно. Якщо так, то кінець. Шукана модель вибирається з часткових описів 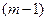-го рівня, на якому досягається мінімальна помилка 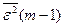. Інакше перехід до конструювання наступного ряду часткових описів. При цьому провадиться добір (селекція) 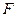кращих описів.

Заключний етап. Рухаючись від кінця до початку і роблячи послідовну заміну перемінних, обчислюються вирази для шуканої моделі у початковому просторі описів.