Основні принципи і загальна схема методу групового урахування АРГУМЕНТІВ
МГУА призначено для розв’язання задач ідентифікації моделей шляхом використання ідеї самоорганізації і механізмів живої природи – схрещування (гібридизацію) і селекцію (відбір).
Нехай є вибірка з 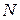 спостережень вхідних векторів
спостережень вхідних векторів 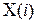 та вихідних
та вихідних 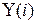 :
:
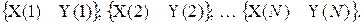
За результатами спостережень треба визначити 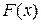 , причому структура моделі
, причому структура моделі 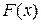 невідома (рис.5.1).
невідома (рис.5.1).
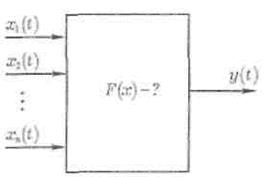
Рисунок 5.1 – Задача ідентифікації моделі
Найбільш повна залежність між входами 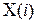 і виходами
і виходами 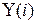 може бути представлена за допомогою узагальненого полінома Колмогорова-Габора.
може бути представлена за допомогою узагальненого полінома Колмогорова-Габора.
Нехай є вибірка 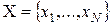 , тоді такий поліном має вигляд
, тоді такий поліном має вигляд
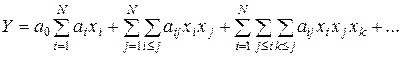 ,
,
де всі коефіцієнти 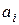 невідомі.
невідомі.
При побудові моделі (при визначенні значень коефіцієнтів) як критерій оптимізації використовується МНК, де критерій регулярності (точності) має вигляд
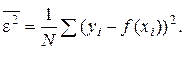
Треба знайти таку модель, для якої 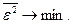
Розглянемо основні принципи та ідеї МГУА.
Принцип множинності моделей:існує множина моделей на даній вибірці, що забезпечують нульову помилку (достатньо підвищувати ступінь полінома моделі). Тобто, якщо є 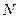 вузлів інтерполяції, то можна побудувати ціле сімейство моделей, кожна з яких при проходженні через експериментальні точки буде давати нульову помилку
вузлів інтерполяції, то можна побудувати ціле сімейство моделей, кожна з яких при проходженні через експериментальні точки буде давати нульову помилку
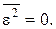
Як правило, ступінь нелінійності беруть не вище 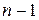 , якщо
, якщо 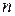 - кількість точок вибірки.
- кількість точок вибірки.
Позначимо через 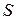 складність моделі (визначається числом членів полінома Колмогорова-Габора).
складність моделі (визначається числом членів полінома Колмогорова-Габора).
Значення помилки 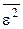 залежить від складності моделі. Причому в міру росту складності спочатку вона буде падати, а потім зростати. Потрібно вибрати таку оптимальну складність, при якій помилка буде мінімальна. Крім того, якщо враховувати дію перешкод, то можна виділити такі моменти:
залежить від складності моделі. Причому в міру росту складності спочатку вона буде падати, а потім зростати. Потрібно вибрати таку оптимальну складність, при якій помилка буде мінімальна. Крім того, якщо враховувати дію перешкод, то можна виділити такі моменти:
1.При різному рівні перешкод залежність 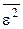 від складності
від складності 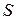 буде змінюватися, зберігаючи при цьому загальну спрямованість.
буде змінюватися, зберігаючи при цьому загальну спрямованість.
2.При збільшенні рівня перешкод величина 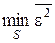 буде зростати.
буде зростати.
|
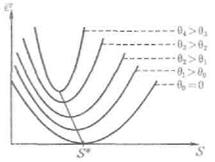
3. З ростом рівня перешкод величина 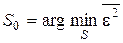 буде зменшуватись (оптимальне значення складності буде зміщатися вліво). Причому
буде зменшуватись (оптимальне значення складності буде зміщатися вліво). Причому 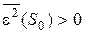 , якщо рівень перешкод не нульовий ( рис. 5.2).
, якщо рівень перешкод не нульовий ( рис. 5.2).
Рисунок 5.2 – Залежність 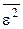
Теорема неповноти Геделя:у будь-якій формальній логічний системі існує ряд тверджень і теорем, які не можна ні опротестувати, ні довести, залишаючись у рамках цієї системи аксіом.
У даному випадку ця теорема означає, що вибірка завжди неповна. Один зі способів подолання цієї неповноти – принцип зовнішнього доповнення. В якості зовнішнього доповнення використовується додаткова вибірка (перевірочна), точки якої не використовувалися при навчанні системи (тобто при пошуку оцінок значень коефіцієнтів полінома Колмогорова-Габора).
Пошук найкращої моделі здійснюється в такий спосіб:
1. Уся вибірка поділяється на навчальну і перевірочну: 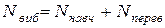 ;
;
2. На навчальній вибірці 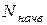 визначаються значення
визначаються значення 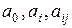 ;
;
3. На перевірочній вибірці 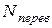 відбираються кращі моделі.
відбираються кращі моделі.
Вихідний вектор має розмірність 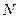 (
( 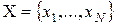 ).
).
Принцип свободи вибору (неостаточності проміжного рішення):
1. Для кожної пари 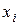 та
та 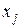 будуються часткові описи (всього
будуються часткові описи (всього 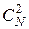 ) виду:
) виду:
- або 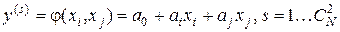 (лінійні);
(лінійні);
- або 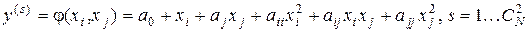 (квадратичні).
(квадратичні).
2. Визначаємо коефіцієнти цих моделей за МНК, використовуючи навчальну вибірку. Тобто знаходимо 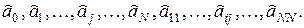
3. Далі на перевірочній вибірці для кожної з цих моделей шукаємо оцінку
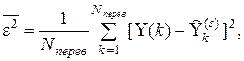
(де 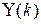 ‑ дійсне вихідне значення в
‑ дійсне вихідне значення в  -тій точці перевірочної вибірки;
-тій точці перевірочної вибірки; 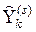 ‑ вихідне значення в
‑ вихідне значення в 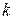 -тій точці перевірочної вибірки відповідно до
-тій точці перевірочної вибірки відповідно до 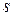 -ої моделі) і визначаємо
-ої моделі) і визначаємо 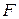 кращих моделей.
кращих моделей.
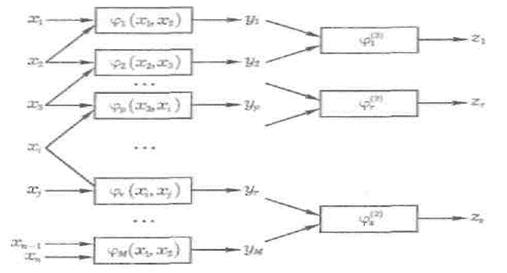 |
Обрані
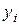 подаються на другий ряд (рис.5.3).
подаються на другий ряд (рис.5.3).
Рисунок 5.3 – Структура багаторядного алгоритму МГУА
Шукаємо
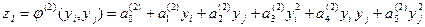 .
.
Оцінка тут така ж, як на першому ряді. Добір кращих здійснюється знову так само, але 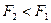 .
.
Процес конструювання рядів повторюється доти, поки середній квадрат помилки буде падати. Коли на шарі 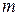 одержимо збільшення помилки
одержимо збільшення помилки 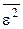 , то припиняємо.
, то припиняємо.
Якщо часткові описи квадратичні і число рядів полінома 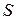 , то одержуємо, що максимальний ступінь полінома
, то одержуємо, що максимальний ступінь полінома 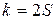 . На відміну від звичайних методів статистичного аналізу, при такому підході можна одержати досить складну залежність, навіть маючи коротку вибірку.
. На відміну від звичайних методів статистичного аналізу, при такому підході можна одержати досить складну залежність, навіть маючи коротку вибірку.
Існує проблема: на першому ряді можуть відсіятися деякі перемінні 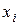 і
і 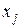 , котрі впливають на вихідні дані.
, котрі впливають на вихідні дані.
У зв’язку з цим запропонована така модифікація: на другому шарі подавати 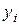 та
та 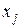 , тобто:
, тобто:
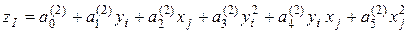 .
.
Це важливо при високому рівні перешкод, щоб забезпечити незміщеність моделей.
Виникає два критерії добору кращих кандидатів часткових описів, які передаються на певному шарі на наступний ряд (шар).
1. Критерій регулярності (точності) 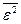
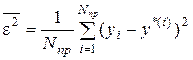 ;
;
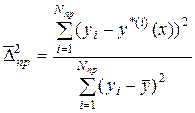 .
.
2. Критерій незміщеності. Усю вибірку, поділяємо на дві частини 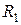 ,
, 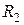 , де
, де 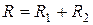 :
:
Перший експеримент:
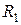 ‑ навчальна вибірка,
‑ навчальна вибірка, 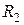 ‑ перевірочна;
‑ перевірочна;
визначаємо виходи моделі 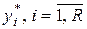 ;
;
Другий експеримент:
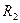 ‑ навчальна вибірка,
‑ навчальна вибірка, 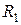 ‑ перевірочна;
‑ перевірочна;
визначаємо виходи моделі 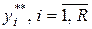 ;
;
і порівнюємо.
Критерій незміщеності:
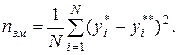
Чим менше 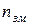 , тим більше незміщеною є модель.
, тим більше незміщеною є модель.
Такий критерій визначається для кожного часткового опису першого рівня і потім знаходиться 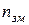 для рівня в цілому для
для рівня в цілому для 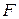 кращих моделей
кращих моделей
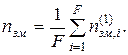
У ряді варіантів 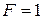 . Аналогічно на другому шарі обчислюємо
. Аналогічно на другому шарі обчислюємо 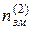 .
.
Процес селекції здійснюється доти, поки цей критерій не перестане зменшуватися, тобто до досягнення умови
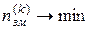 .
.
Переваги метода МГУА
1. можна відновити невідому довільну складну залежність по обмеженій вибірці. Число невідомих параметрів моделі може бути більше, ніж число точок навчальної послідовності.
2. Можливість адаптації параметрів моделі при одержанні нових даних експериментів.
Дата добавления: 2016-02-20; просмотров: 1416;
