Алгоритмизация процесса решения задач

Алгоритмы: понятие, свойства, способы записи, виды

В своей повседневной деятельности человеку постоянно приходится сталкиваться с набором определенных действий, правил, цель которых состоит в достижении некоторого результата. Нам следует придерживаться вполне определенного комплекса правил(инструкций), например, для того, чтобы перейти проезжую часть, на которой не предусмотрена регулировка движения (подойти к краю проезжей части; посмотреть влево, в том случае, если мы видим близко приближающийся к нам транспорт, то ожидаем его проезда, если же нет транспорта, то перемещаемся на середину проезжей части; посмотреть вправо, в том случае, если мы видим близко приближающийся к нам транспорт, то ожидаем его проезда, если же нет транспорта, то завершаем переход проезжей части) или оказать первую медицинскую помощь, и т.п. Таких примеров можно привести неограниченное количество. Их часто называют алгоритмами.

Понятие "алгоритм" связано с именем математика древности Аль-Хорезми (IX в.н.э.), который разработал и изложил правила (сегодня мы называем их алгоритмами) выполнения четырех арифметических действий над числами, представленными в десятичной форме.

Под алгоритмом следует понимать систему точных предписаний(правил), заданных вычислительным процессом, и обладающих некоторыми определенными свойствами. Всякий алгоритм предполагает наличие некоторого исходного данного (или совокупности данных), определяющего в дальнейшем получение того или иного результата. Заметим, что множество входных(исходных) данных и множество результатов часто совпадают. Например, в алгоритмах арифметических вычислений и исходные данные, и результаты - числа. Но в ряде случаев исходные данные и результаты могут оказаться совершенно разной природы. Например, во многих задачах управления в качестве исходных данных для алгоритмов, решающих задачи планирования, выступают числа, выражающие производительность, мощность предприятий, запасы ресурсов, результатом же может оказаться информация, приводящая к решению построить новый завод.

Алгоритм, предназначенный для выполнения его на ЭВМ, специальных машинах-автоматах должен обладать рядом свойств. Рассмотрим основные четыре из них:

1. Дискретность, т.е. пошаговый характер определяемого алгоритмом процесса. Каждый шаг процесса, описываемого алгоритмом, разбивается на отдельные шаги, каждый их которых состоит в выполнении некоторого определенного действия. Алгоритм должен быть потенциально осуществим, т.е. заканчиваться после конечного числа шагов.

2. Определенность, т.е. при описании действий, составляющих алгоритм, следует придерживаться четкости, понятности и однозначности. Разрабатывая алгоритм необходимо предусматривать все возможные ситуации, которые могут возникнуть в ходе решения задачи, а также исключать "домысливание" своих действий его исполнителем.

3. Массовость алгоритма заключается в том, чтобы он был применим к некоторому множеству различных комбинаций исходных данных в пределах одной задачи, поскольку нет целесообразности в разработке алгоритма, предназначенного для обработки только одного сочетания исходных данных.

4. Результативностьозначает, что в итоге работы алгоритма должен быть конечный результат, являющийся решением определенной задачи.

Любой алгоритм становится алгоритмом лишь тогда, когда он обретает какую-либо форму. Существует два наиболее распространенных способа описания алгоритма:

а) обычная словесная запись команд, которые в совокупности образуют алгоритмический язык ;

б) запись алгоритма в виде блок-схемы.

БЛОК-СХЕМА

Выше приведенная форма записи алгоритма не всегда является удобной для человека, особенно при достаточно больших алгоритмах. Главным недостатком этой формы является отсутствие наглядности в переходах между отдельными шагами алгоритма. Этого недостатка лишена форма записи алгоритма в виде блок-схемы.

Блок-схема позволяет в четкой двухмерной графической форме наглядно изложить структуру алгоритма, что значительно упрощает задачу его разработки и контроля. Приведем основные геометрические обозначения (блоки), принятые в соответствии с ГОСТ 19.003-80 “Символы в схемах алгоритмов и программ”, с помощью которых можно описать любой вычислительный процесс:

- блок начала или конца алгоритма;

- операционный блок;

- блок ввода-вывода данных;

- логический блок (проверка условий);

- соединитель;

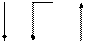- линии потока(ветви);

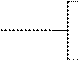- комментарий.

Существуют определенныеправила составления блок-схем:

1) Блок-схема должна иметь точку начала и точку окончания. От точки начала блоки располагаются сверху вниз и слева направо.

2) Между собою блоки связываются с помощью линий потока (ветвей), определяющих последовательность вычислительного процесса.

3) Из каждого прямоугольника и параллелограмма (кроме конца алгоритма) должна выходить ровно одна ветвь.

4) В каждый прямоугольник и параллелограмм (кроме начала алгоритма) должна входить хотя бы одна ветвь.

5) В каждый ромб должна входить хотя бы одна ветвь, а выходить из него ровно две ветви, помеченные словами “ДА” и “НЕТ”, либо символами “+” и “-” соответственно.

6) Блоки рекомендуется идентифицировать (присваивать номера) в порядке расположения их в блок-схеме.

7) В том случае, когда обилие ветвей загромождает блок-схему, следует применять соединители, внутри которых указываются идентификаторы соединяемых блоков.

Правильно составленной считается такая блок-схема, в которой, следуя из точки начала можно прийти по каждому из направлений линий потока в точку окончания алгоритма. И наоборот, если в какой-то блок нельзя попасть из точки начала или какого-либо блока нельзя прийти в точку окончания алгоритма, то такая блок-схема составлена неверно.

Существует три основных вида алгоритма - линейный, разветвляющийся, циклический.