Анализ интенсивностей дифракционных максимумов. Атомный фактор и структурная амплитуда
Согласно кинематической теории интенсивность рассеяния одним атомом характеризуют его атомным фактором. Атомным фактором f называется отношение амплитуды волны, рассеянной атомом, к амплитуде волны, рассеянной электроном
f = Eат/Eэл . (2.38)
Поскольку интенсивность рассеянных лучей пропорциональна квадрату амплитуды (I~E2), то атомный фактор определяет интенсивность рассеяния атомом.
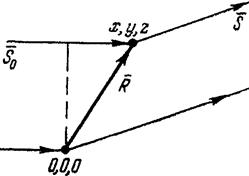
Рис. 2.15. К выводу формулы для структурной амплитуды.
Интенсивность лучей, рассеянных одним электроном в том или ином направлении, различна. Такое направленное рассеяние, или поляризация рассеянной волны, связана с направлением вынужденных колебаний электрона и определяется формулой Томпсона [2]:
× 
× 
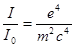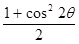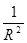, (2.39)
где R – расстояние от рассеивающего электрона; 2q – угол между направлением падающего пучка и пучка рассеяния; I и I0 – интенсивность падающего и рассеянного пучков.
В атоме электроны не сосредоточены в одной точке, а распределены вокруг ядра в оболочке, размеры которой сравнимы с длиной волны. При расчете рассеивающей способности атома необходимо учесть интерференцию всех волн, рассеянных отдельными электронами. Если атом содержит Z электронов, мгновенное расположение которых в пространстве описывается радиусом-вектором ri, то мгновенное значение амплитуды, рассеянной атомом, будет равно [2]:
Eат =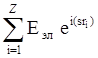 
, (2.40)
где sri – учитывает разность фаз, возникающую между волнами, рассеянными
i-электроном и электроном в начале координат.
Зная распределение (плотность) электронного облака свободного атома, амплитуду рассеяния Eат можно рассчитать теоретически. Она зависит от угла рассеяния и длины волны падающего излучения. В связи с этим величина атомного фактора f также будет зависеть от этих величин. Из опытных данных величину f можно получить, измеряя усредненные, например, по какому-то элементу объема, амплитуды рассеяния. Значения fтеор и fэксп достаточно хорошо совпадают [2]. Для различных атомов они сведены в таблицы, дающие значения атомных факторов как функцию sinq/l.
В том случае, когда рассеяние рентгеновских лучей происходит в некотором объеме, то суммарная амплитуда луча дифракции будет зависеть от числа рассеивающих атомов, приходящихся на этот объем и их взаимного расположения, т.е. от числа атомов базиса и их координат.
Допустим, что в элементарной ячейке содержится 2 атома (рис.2.15). Начало координат поместим в один из них, другой имеет координаты x, y, z. Если S0 иS единичные вектора на направлении падающего луча и луча рассеянного, то разность хода равна:
(R[S – S0]) = d (2.41)
или разность фаз составит:
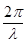d = j (2.42)
Подставив значение d из (2.41) и (S– S0) из общего интерференционного уравнения (2.28) получим:
j = 2p (HR) = 2p (Hx +Ky+Lz) (2.43)
Амплитуда рассеянной волны с такой разностью фаз запишется как:
F = fo eij (2.44)
Если в элементарной ячейке не 2 атома, а j базисных атомов, то
F =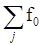 
eij (2.45)
Здесь f0 примерно соответствует амплитуде рассеяния одним атомом базиса, или атомному фактору, поэтому для разных базисных атомов суммарная амплитуда рассеяния одной элементарной ячейкой равна
F=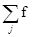 
j e2pi (Hx+Ky+Lz) , (2.46)
где x, y, z – координаты атомов базиса; fj – атомные факторы базисных атомов; H, K, L – индексы интерференции, определяющие, в частности, направление, в котором рассматривается рассеяние; j – число базисных атомов.
Величина F получила название структурной амплитуды. Структурная амплитуда показывает во сколько раз суммарная амплитуда лучей, рассеянных группой атомов базиса, больше амплитуды рассеяния одним электроном. Каждому отражению H, K, L соответствует своя структурная амплитуда. Величина, равная квадрату структурной амплитуды, называется структурным множителем.
Выражение для структурной амплитуды может быть записано и в другой форме. По формуле Эйлера eix = cos x + i sin x, поэтому можно записать:
F =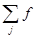 
j cosjj + i 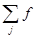j sinjj , (2.47)
где jj = 2p (Hxj + Kyj +Lzj).
Дата добавления: 2016-02-04; просмотров: 1749;