Отражение рентгеновских лучей сложной элементарной ячейкой
Как следует из уравнения Вульфа–Брегга, направления дифракционных лучей всегда будут совпадать (при рассеянии сложной или простой ячейкой), если направление падающего пучка неизменно. Направления пучков дифракции определяются исключительно параметрами элементарной ячейки и S0. Однако, интенсивность этих лучей будет зависеть от плотности атомов в отражающей плоскости, разности фаз лучей отраженных ближайшими атомными плоскостями, т.е. дифракционные лучи, идущие по одному и тому же направлению от примитивной и сложной ячеек, будут различными по интенсивности.
Этот результат можно наглядно объяснить, рассматривая сложную элементарную ячейку как составную, образованную из некоторого числа примитивных ячеек, вставленных друг в друга. Соответственно, любая сложная структура может быть представлена составленной из простых решеток или “подрешеток”, содержащих атомы только в узлах и вставленных друг в друга. Например, объемноцентрированную ячейку можно представить в виде двух примитивных кубических ячеек, одна из которых сдвинута относительно другой на половину диагонали куба (рис.2.13,а).
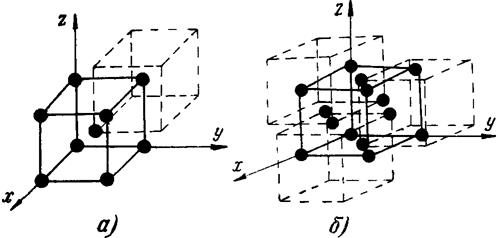
Рис.2.13. Базис объемно- (а) и гранецентрированной (б) ячеек.
Гранецентрированная ячейка образуется четырьмя примитивными (рис.2.13,б), из которых три сдвинуты относительно начальной на половину диагонали каждой из трех взаимно перпендикулярных граней.
Таким образом, любую сколь угодно сложную структуру, можно разложить путем параллельного переноса на N равных простых решеток, каждая из которых содержит атомы только в узлах.
Поскольку все примитивные ячейки, составляющие сложную ячейку, строго одинаковы по размерам и ориентации, отраженные лучи для каждой из них в отдельности пойдут по одинаковым направлениям. Если мы теперь из простых решеток образуем сложную, то отраженные лучи, идущие от отдельных решеток, будут интерферировать между собой. В результате их сложения направление лучей остается тем же, а изменится только их интенсивность.
Очень важен также и обратный вывод – он заключается в том, что рассматривая геометрию дифракционной картины, т.е. расположение интерференционных линий, пятен и т.д. можно в общем случае установить только размеры и форму элементарной ячейки кристалла. Распределение атомов в ячейке можно определить достоверно, только учитывая интенсивность этих рефлексов.
Рассмотрим отражение рентгеновских лучей на кристаллах с примитивной и сложной элементарными ячейками (рис.2.14) и установим различие между картинами интерференции, возникающими в том и другом случае. Возьмем 2 кристалла: первый с примитивной ячейкой (рис.2.14,а) и второй с более сложной, например, гранецентрированной элементарной ячейкой (рис.2.14,б). Период идентичности для обеих решеток один и тот же
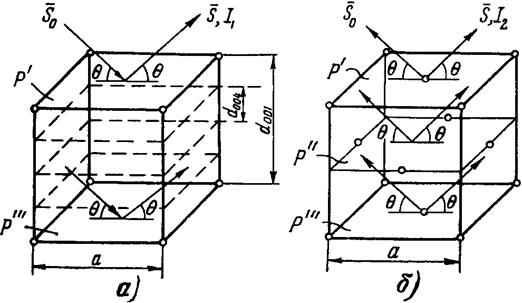
Рис. 2.14. Отражение рентгеновских лучей примитивной (а) и
сложной (б) ячейками.
и равен a. Пусть на тот и другой кристалл падает по одному и тому же направлению пучок рентгеновских лучей. Рассмотрим, как может меняться интенсивность лучей дифракции при переходе от простой структуры к сложной для какого-то семейства плоскостей кристалла.
1. Пусть пучок рентгеновских лучей образует с плоскостью (001) примитивной ячейки угол q1, удовлетворяющий условию Вульфа–Брегга:
2d001×sinq1=l,
где при n=1 разность хода равна l и H, K, L не имеют общего множителя.
В этом случае лучи, отраженные плоскостями P¢ и P¢¢¢ примитивной ячейки, совпадут по фазе. В результате интерференции их амплитуды сложатся и усиленные отраженные лучи будут фиксироваться на фотопленке в виде пятна или линии с индексами 001.
В гранецентрированной решетке параллельно плоскостям P¢ и P¢¢¢ существует промежуточная плоскость P¢¢, проходящая через атомы в центрах граней. В этом случае разность хода лучей, отраженных соседними плоскостями P¢ и P¢¢ составит l/2. Такие лучи противоположны по фазе лучам P¢ и P¢¢¢ и будут полностью гаситься. Поскольку любая пара плоскостей (001) в гранецентрированной ячейке разделена такой промежуточной плоскостью, то промежуточных плоскостей столько же, сколько и основных. Поэтому кристалл с объемноцентрированной решеткой совсем не дает отражений первого порядка от плоскости (001), а также от эквивалентных им плоскостей (100), (010) и т.д. Как следствие – линия или пятно 100 на рентгенограмме этого кристалла будет отсутствовать.
2. Следующее отражение от тех же самых плоскостей станет возможным при угле q2 и n=2, когда выполняется соотношение: 2d001×sinq2 = 2l или 2d002×sinq2 = l. На рентгенограмме примитивной ячейки этому условию будет соответствовать своя линия или пятно с индексами 002.
В гранецентрированной ячейке разность хода для соседних плоскостей P¢ и P¢¢ при угле q2 теперь равна l. В этом случае лучи, отраженные от плоскостей P¢–P¢¢¢ и P¢–P¢¢, совпадут по фазе, а интенсивность суммарного луча, пропорциональная квадрату амплитуды, станет в 4 раза больше интенсивности отражения от плоскостей примитивной ячейки. Соответственно на рентгенограмме поликристалла с гранецентрированной ячейкой появится очень яркая интерференционная линия 002, отвечающая углу отражения q2 .
Из сказанного следует, что интенсивность лучей, отраженных от одних и тех же плоскостей примитивной и сложной ячеек различны, а именно: некоторые отражения в сложной ячейке гасятся (пятна 001 в рассмотренном случае), другие усиливаются (пятна 002).
Базис ячейки
К аналогичному выводу можно прийти и в том случае, если рассматривать это явление не как отражение, а как дифракцию рентгеновских лучей на атомах элементарной ячейки или на базисных атомах.
Определим, сколько атомов приходится на одну элементарную ячейку и каково их расположение. Примитивная ячейка может быть охарактеризована одним атомом. За координаты его выбираются [[000]]. Поскольку, в простой пространственной решетке каждый узел одновременно принадлежит восьми соседним элементарным ячейкам и таких узлов в вершинах примитивной элементарной ячейки восемь, то на долю одной ячейки приходится 1 узел. Таким образом, узел [[000]] определяет число (и координаты) атомов, приходящихся на одну примитивную ячейку. Это базис данной ячейки. Запишем базис примитивной ячейки как (000).
Объемноцентрированная элементарная ячейка, которую можно представить составленной из двух примитивных (рис.2.13,а), имеет 2 базисных атома. Один из них определяет не сдвинутую ячейку и имеет координаты [[000]], второй характеризует ячейку, смещенную на половину диагонали куба, и имеет координаты [[ 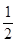
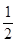
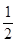 ]]. Таким образом, базис объемноцентрированной ячейки (000,
]]. Таким образом, базис объемноцентрированной ячейки (000, 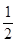
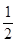
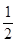 ).
).
Гранецентрированная ячейка, которую можно разложить на 4 примитивных (рис.2.13,б), имеет 4 базисных атома. За базисный атом в каждой из трех сдвинутых примитивных ячеек выбираются ближайший к началу координат. Тогда базис гранецентрированной ячейки запишется как (000, 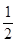 0
0 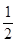 , 0
, 0 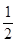
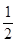 ,
, 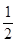
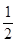 0).
0).
При рассмотрении пространственной решетки также можно прийти к выводу, что на одну гранецентрированную элементарную ячейку приходится 4 атома, а на одну объемноцентрированную 2, если учесть что к одной элементарной ячейке относится 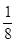
 атома в вершине,
атома в вершине,  атома на ребре,
атома на ребре, 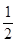 атома на грани и 1 в центре объема элементарной ячейки. Таким образом, число атомов в базисе всегда равно числу атомов, приходящихся на одну элементарную ячейку. Поэтому при рассмотрении дифракции рентгеновских лучей при их прохождении через кристалл, можно говорить о рассеянии рентгеновских лучей группой атомовбазиса.
атома на грани и 1 в центре объема элементарной ячейки. Таким образом, число атомов в базисе всегда равно числу атомов, приходящихся на одну элементарную ячейку. Поэтому при рассмотрении дифракции рентгеновских лучей при их прохождении через кристалл, можно говорить о рассеянии рентгеновских лучей группой атомовбазиса.
Дата добавления: 2016-02-04; просмотров: 1589;
