Дифракция рентгеновских лучей в кристаллах

Напомним, что дифракция – это явление или эффект, который является результатом двух процессов: когерентного рассеяния и интерференции рассеянных волн. В результате этих процессов амплитуда и, следовательно, интенсивность рассеянных волн меняется в зависимости от направления их распространения. Суммарная дифракционная картина определяется с одной стороны тем, каково строение объекта, являющегося источником рассеянных волн, и с другой – спектральным составом излучения.

Проведем анализ дифракционного эффекта, создаваемого при взаимодействии рентгеновских лучей с отдельным атомным рядом и трехмерным кристаллом при постоянной длине волны. Кинематическая теория рассеяния при рассмотрении дифракции на кристалле вводит некоторые ограничения, основные из которых следующие:

а) атомы принимаются неподвижными;

б) атомы рассматриваются как точечный источник рассеянных волн;

в) амплитуда рассеянных волн во всех направлениях от одного атома одинакова.

Эти допущения упрощают рассуждения и практически не сказываются на виде дифракционной картины.

Рассмотрим атомный ряд с периодом идентичности, равным a (рис.2.7), и примем, что на него падает пучок монохроматических λ=сonst рентгеновских лучей. Угол падения их обозначим через a₀. Атомы примем за идентичные.

Учитывая, что расстояние между атомами в кристалле порядка 2–3 Å, а размеры исследуемых кристаллов обычно не меньше 0,2–0,3 мм (т.е. миллионы Å), любой атомный ряд в кристалле можно считать бесконечным. Таким образом, принимаем рассматриваемый нами атомный ряд бесконечным.

Расстояние от кристалла до фотопленки в камерах обычного типа 30–40 мм и более, т.е. много больше размера кристалла. Тогда лучи, идущие от разных атомов ряда, в определенном направлении можно считать практически параллельными. Лучи, рассеянные отдельным атомом ряда, сферически распространяются во все стороны и интерферируют между собой. Если в каком-нибудь направлении разности фаз между соседними лучами составляют целое число длин волн, то происходит сложение их амплитуд, и в

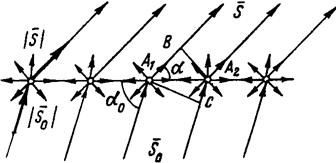
Рис. 2.7. Рассеяние рентгеновских лучей на атомном ряде.

этом направлении наблюдается так называемый интерференционный максимум. Если разность фаз соседних лучей не равна ml, то луч будет ослаблен или совсем погашен. Практически, в последнем случае в результате наложения колебаний происходит полное исчезновение электромагнитного поля.

Рассмотрим интерференцию рассеянных волн для какого-то направления максимума интерференции, составляющего с атомным рядом угол a (рис.2.7). Усиление рассеянных рентгеновских волн будет наблюдаться в тех случаях, когда разность хода двух соседних лучей равна целому числу длин волн, т.е. если

A₁B – A₂C = ml , (2.19)

где m = 0,1,2,3…, A₂C – разность хода падающих лучей; A₁B – разность хода вторичных рассеянных лучей.

Подставляя значение отрезков A₁B и A₂B, получим:

a (cosa – cosa₀) = ml , (2.20)

где m – определяет порядок дифракции. В направлениях, в которых это условие соблюдается, рассеянные лучи дают максимумы интенсивности, в других направлениях они практически полностью погашаются.

Полученное уравнение, названное условием Лауэ, позволяет определить направление всех дифракционных максимумов от атомного ряда, если известны расстояния между атомами a, длина волны лучей l и угол падения рентгеновских лучей a₀:

cos a = m + cos a₀ . (2.21)

Но выражение (2.21) есть не что иное, как уравнение конуса (рис.2.8) в тригонометрической форме.

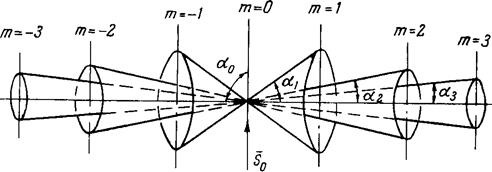
Рис. 2.8. Графическое изображение уравнения Лауэ для одномерного ряда.

В полученном семействе конусов рассеяния каждый конус и, соответствующий ему угол раствора a, связаны с определенным значением целого числа m. Принимая во внимание, что размеры рассеивающего объекта очень малы по сравнению с расстоянием его до фотопластинки, можно считать, что конуса, соответствующие разным m, имеют общую вершину.

Осью всех этих конусов является атомный ряд, а вершина находится в точке пересечения первичного пучка рентгеновских лучей с атомным рядом (рис.2.8). Для m=0 a=a₀, т.е. направление первичного пучка рентгеновских лучей всегда совпадает с образующей нулевого конуса.

Очевидно, уравнение (2.21) будет выполнимо не при всяких соотношениях m и l. Рассмотрим, при каких условиях не выполнимо уравнение Лауэ, т.е. при каких условиях не будет наблюдаться явление дифракции. Косинусы a и a₀ всегда должны быть по абсолютной величине меньше или равны 1, и максимально возможное значение |ml/a|, очевидно, будет равно

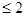|m |_max = |cos a - cos a₀|_max , (2.22)

то есть l£2a/m, или при m=1 l£2a. Таким образом, для получения дифракционной картины необходимо, чтобы l»2a. Величина a обычно порядка нескольких ангстрем. Следовательно, и l не может быть больше этой удвоенной величины. Если, наоборот, l будет очень мала, получим громадное количество дифракционных максимумов, и они будут сливаться.

Исходя из соотношения Лауэ, можно установить число всех возможных дифракционных конусов при заданном l, a и a_0. Пусть угол падения a₀=90°, т.е. cosa₀=0, тогда поскольку |ml/a|£1, число дифракционных конусов определяется соотношением между l и a. При l=1,54 Å и a »5 Å величина m не может быть больше трех, т.е. будет иметь место всего лишь семь конусов рассеяния, отвечающих m = –3, –2, –1, 0, 1, 2, 3.

Рассмотрим теперь трехмерную систему атомов, предполагая, что все атомы находятся в узлах решетки. Эффект дифракции в этом случае будет аналогичным тому, который происходит в кристаллах.

Рассматривая дифракцию рентгеновских лучей вдоль трех различных кристаллографических направлений, не находящихся в одной плоскости, получим 3 независимые уравнения Лауэ, являющиеся условием дифракции рентгеновских лучей в кристаллах. Обычно берут направление вдоль основных кристаллографических осей a, b, c.

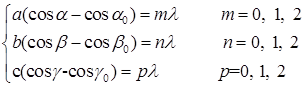(2.23)

Здесь b₀ и g₀ – углы между падающим лучом и осями y и z;

b и g – углы между дифракционным лучом и теми же осями;

b и c – периоды вдоль осей y и z соответственно.

Так же, как и для отдельного атомного ряда, дифракция на трехмерной решетке будет возможна только в том случае, когда длина волны рентгеновского луча сравнима с периодом решетки. При этом одновременно должны выполняться все три условия Лауэ.

Дифракционная картина, создаваемая атомной сеткой, резко отличается от той, которая создается атомным рядом. Дифракционные лучи теперь пойдут не по сплошным коническим поверхностям, а по дискретным направлениям и при пересечении с рентгеновской пленкой дадут отдельные точки.

Это легко представить, рассмотрев графическое решение системы уравнений Лауэ. Каждое из уравнений определяет направление луча дифракции как конус, осью которого является одна из осей X, Y или Z (рис.2.8). Общим решением системы является пересечение всех трех конусов по одной прямой. Такая прямая и определяет направление луча дифракции на трехмерной решетке. Однако одновременное пересечение трех конусов по одному направлению не всегда возможно (рис. 2.9).

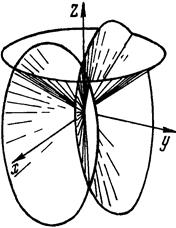
Рис. 2.9. Графическое изображение уравнений Лауэ для трехмерной решетки.

В кристалле, при облучении монохроматическим пучком лучей и неизменном его положении, такой случай может иметь место очень редко. Добиться в какой-то момент выполнения трех условий можно:

1) непрерывно меняя длину волны падающего пучка (или, что равносильно, беря излучение со сплошным спектром) и

2) при постоянной l, меняя углы a₀, b₀, g₀, т.е. меняя положение кристалла.

При постоянной l и неподвижном кристалле можно не получить ни одного дифракционного луча, а следовательно, и пятен на рентгенограмме будет очень мало.