Дифракция световых волн.

Ньютон: свет - поток корпускул.

Гюйгенс, Френель: свет – волна.

преграда: круглое отверстие, диск и др.

Объяснить это явление можно с помощью принципа Гюйгенса-Френеля:

каждая точка пространства, до которой дошел фронт волны в данный момент времени, становится источником вторичных волн, огибающая которых дает фронт волны в новый момент времени; вторичные волны – когерентные и при наложении их друг на друга образуют интерференционную картину.

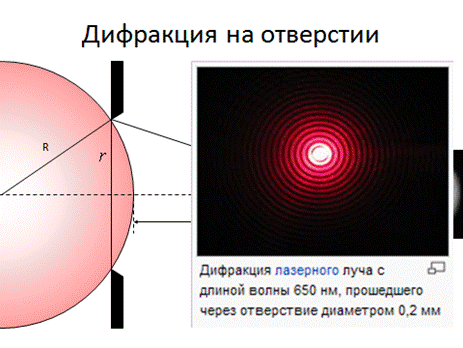
Явление огибания волнами встречающихся препятствий, соизмеряемых с длиной волны, называется дифракцией волн (для световых волн – дифракцией света, при этом происходит отклонение от законов геометрической оптики).

– дифракция Френеля (в ближайшей волновой зоне)

– дифракция Фраунгóфера (в дальней волновой зоне)

5. Дифракция Френеля на круглом отверстии и диске

Для описания дифракции в ближней зоне (дифракция Френеля) Френель предложил метод зон (метод зон Френеля).

Суть метода заключается в следующем.

Фронт волны разбивается на небольшие участки (зоны Френеля), расстояние от краев которых до точки наблюдения отличается на .

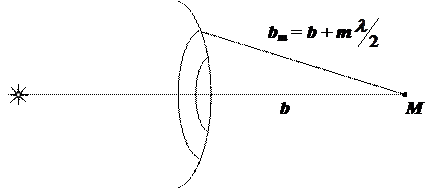b_m = b + m , m = 0, 1, 2, … (2-1)

Зоны Френеля выполняют роль источников вторичных волн.

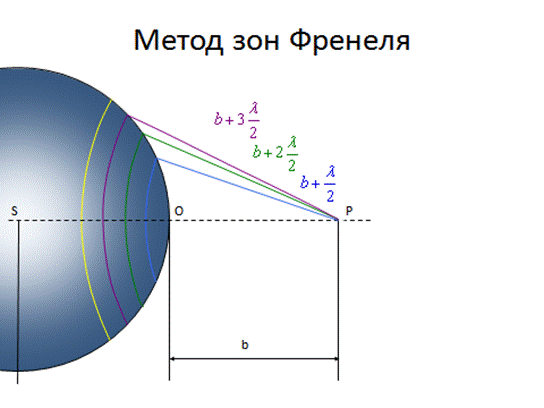
Ввиду малости зон Френеля будем считать амплитуду всех волн, идущих от одной зоны, приблизительно одинаковой и обозначим их как .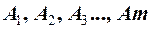

Так как в точку наблюдения M света от каждой следующей зоны будет приходиться все меньше и меньше, тогда ряд амплитуд будет представлять собой убывающую прогрессию

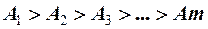
Колебания от двух соседних зон будут приходить в точку наблюдения M в противофазе и тогда при наложении друг на друга результирующая амплитуда может быть вычислена:

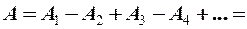
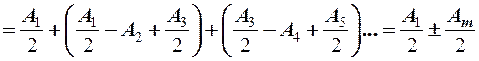
Если преград нет – полностью открытый фронт волны, тогда: 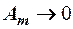, следовательно .

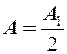Размер зон Френеля?

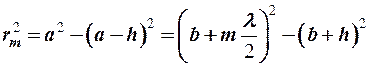
Пренебрегая величинами второго порядка малости 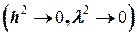, получим

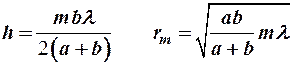(2-2)

Для оценки 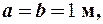тогда

- прямолинейность распространения света!

Если на пути светового луча встречается преграда в виде круглого отверстия, в которое попадает m зон Френеля, тогда из (2-2) имеем:

(2-3)

Круглое отверстие

m – четное m – нечетное

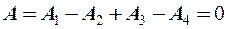
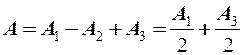
Min max

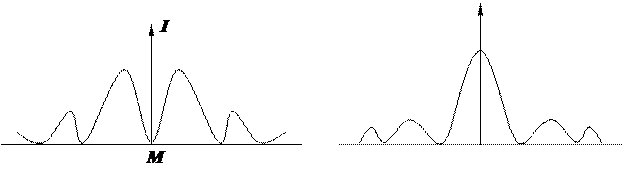– открытый фронт: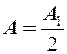

– круглое отверстие: ­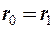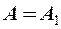 в 2 раза

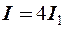­ в 4 раза

Зонная пластинка

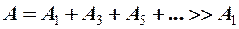
Круглый диск

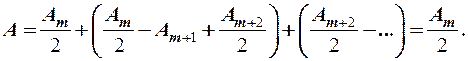
пятно Пуассона !

Из формулы (2-3) следует, что, например, для плоского фронта волны, когда а → ∞ имеем

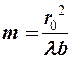
Тогда, если , то наблюдается дифракция Френеля;

Если , это соответствует геометрической оптике;

Если , это соответствует дифракции Фраунгофера.