Давление и импульс электромагнитных волн.

Гипотеза о световом давлении на отражающие и поглощающие тела впервые была высказана И. Кеплером (1619г.) для объяснения отклонения хвостов комет, пролетающих вблизи Солнца. Впоследствии Дж. К. Максвелл (1873г.) предсказал величину светового давления, которая оказывается очень малой даже для света, испускаемого такими мощными источниками света как Солнце или электрическая дуга. При проведении измерения в земных условиях действие светового давление оказывается в тысячу раз меньше действия побочных факторов, основными из которых является конвекционные токи и радиометрические эффекты.

Впервые экспериментальное исследование давления света на твердые тела впервые было проведено П. И. Лебедевым в 1899г. Им же в 1910г было измерено давление на газы.

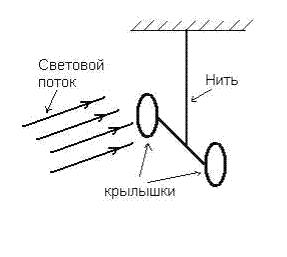
Рис. 1.13.

Основную часть прибора П. И. Лебедева для измерения давления света составляли лёгкие крылышки диаметром 5мм, подвешиваемые на упругой нити (рис.1.13) внутри вакуумированного сосуда. Крылышки изготавливались из различных металлов, слюды и их можно было заменять при проведении экспериментов. На крылышки с помощью системы линз, на показанной на рисунке, направлялся свет от сильной электрической дуги . В результате воздействия света на крылышки нить закручивалась и крылышки отклонялись . Опыты П. И. Лебедева полностью согласовывались с электромагнитной теорией Максвелла.

Явление давления света состоит в том, что при поглощении электромагнитной волны в некотором теле ему передаётся импульс со стороны волны. Для оценки величины давления электромагнитных волн, таким образом, необходимо оценить импульс (количество движения), переносимый волной.

Рассмотрим следующий пример. Пусть плоская электромагнитная волна падает перпендикулярно на плоскую поверхность некоторого слабо проводящего тела со значениями диэлектрической и магнитной проницаемостей, равными единице , т.е. (=1;(=1 .

В соответствии с уравнениями Максвелла (1.1b) в облучаемом теле возбудится ток, плотность которого может быть вычислена по формуле:

.

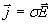Магнитное поле волны будет действовать на ток с силой, величину которой в расчете на единицу объёма тела можно найти по формуле Лорентца:

.

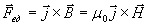(1.34)

Ввиду взаимной ортогональности векторов напряжённости электрического и магнитного полей волны упрощается расчет величины искомой силы:

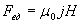
Поверхностному слою тела, объём которого 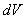, сообщается в единицу времени импульс 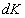в соответствии со вторым закона Ньютона, равный:

.

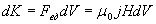(1.35)

В том же слое в единицу времени поглотится (выделится в виде тепла) энергия электромагнитной волны, равная:

.

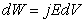(1.36)

Из выражений (1.35) и (1.36) с учетом соотношения между амплитудами электрического и магнитного полей плоской гармонической волны (1.11b) следует, что:

,

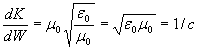где 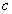- скорость света в вакууме.

Отсюда следует, что плоская электромагнитная волна с плотностью энергии 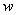имеет импульс 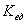в единице объёма, переносимый плоской электромагнитной волной за единицу времени, определяемый по формуле:

.

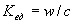(1.37)

В курсе механики³ уже встречалось похожее соотношение между импульсом и энергией релятивистских частиц с нулевой массой покоя. Подобное совпадение не удивительно, ибо согласно современным представлениям электромагнитная волна представляет собой поток обладающих нулевой массой фотонов, движущихся со скоростью света.

Из выражения (1.26b) следует, что поток энергии и импульс в единице объёма электромагнитной волны связаны между собой:

.

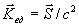(1.38)

Итак, для оценки давления электромагнитной волны надо подсчитать импульс, передаваемый телу за единицу времени со стороны волны, падающей на единичную площадку поверхности тела. Такая сила, как известно, и есть давление электромагнитной волны.

Если 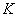импульс электромагнитной волны в единице объёма, то в единицу времени единичной площадке на поверхности полностью поглощающего тела в соответствии с (1.37) будет передан импульс, содержащейся в объёме параллелепипеда, имеющего единичную площадь основания и высоту :

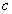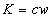
Расчет конкретного значения давления электромагнитной волны зависит от состояния поверхности тела, которое она облучает. Так, для полностью отражающего тела (зеркальной поверхности) импульс 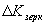, передаваемый телу, определяется изменением импульса 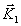электромагнитной волны до отражения и после отражения :

.

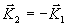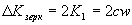Из этих выражений следует, что давление на поверхность полностью поглощающего волну тела в два раза меньше давления на зеркально отражающую поверхность того же тела.

Таким образом, в зависимости от состояния отражающей поверхности (зеркальной, поглощающей или занимающей среднее положение между указанными крайними случаями) давление электромагнитной волны 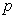может быть оценено с помощью следующего соотношения:

.

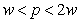(1.39)

При рассмотрении давления плоской гармонической волны необходимо осознавать, что давление 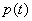представляет собой величину, зависящую от времени и для волн с большой частотой , например, световых с частотой 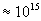колебаний в секунду, частота пульсаций давления оказывается того же порядка 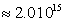. По этой причине для характеристики давления вводят понятие среднего давления 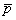, по аналогии определяемого по формуле (1.31a), в которую вместо 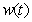надо подставить .

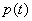Рассчитаем среднее давление плоской гармонической волны с амплитудой 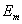, падающей на зеркально отражающую поверхность тела. Тогда, с помощью (1.9), (1.25b) получаем:

,

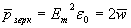(2.40a)

где 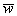- среднее значение плотности энергии электромагнитной волны.

Аналогично может быть получена оценка давления излучения на поглощающее тело:

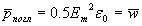
(2.40b)

Проведенный расчет среднего давления позволяет переписать соотношение (2.39) для оценки среднего давления при облучении электромагнитной волной тела:

.

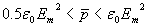(2.41)

Расчет давления электромагнитных волн по этим формулам приводит к очень малой его величине даже для очень мощных источников электромагнитных волн. Как показывают расчеты, подтвержденные в эксперименте, для светового источника мощностью в миллион свечей давление составляет на расстоянии 1м от источника всего лишь - 10^-7ПА.

Необходимо отметить, что давление света не всегда имеет достаточно малое значение. Так, давление сфокусированного лазерного излучения на поверхность тонкой металлической пластинки может привести к её пробою, т.е. к появлению отверстия в пластинке. Давление внутри горячих звёзд играет существенную роль при их взрывах. Если температура внутри звезды достигает величины 10¹²K⁰, то световое давление сравнивается по величине с давлением плазмы, из которой состоит звезда.

Световое давление играет большую роль в астрофизических процессах. Световое давление наряду с давлением газов обеспечивает стабильность звёзд, противодействуя силам гравитационного сжатия. В атомной физике к эффекту светового давления близки процессы передачи части импульса от высокоэнергетического фотона электронам атомов вещества, на которых происходит их рассеяние (эффект Комптона).