Дифракция как отражение

Пусть некоторый узел обратной решетки [[HKL]] попадает на сферу Эвальда. Соответствующая ему плоскость в кристалле с индексами (hkl) располагается нормально H(рис.2.11).

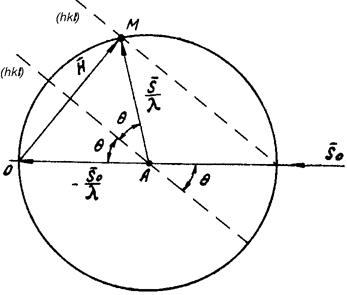
Рис. 2.11. Дифракция как отражение.

Проведем в обратной решетке через центр сферы плоскость, параллельную (hkl). Поскольку вектор H всегда перпендикулярен плоскости (hkl), то угол при вершине OAM, будет разделен надвое. Из этого следует, что углы между падающим лучем S₀и плоскостью (hkl), а также между отраженным лучем и (hkl) всегда равны между собой. На основании этого (hkl) можно рассматривать как плоскость, отражающую рентгеновские лучи, и процесс дифракции можно описывать как отражение рентгеновских лучей от семейства соответствующих плоскостей кристалла.

Действительно, в кристалле всегда можно найти плоскость, которая ориентирована к лучу дифракции как плоскость отражения. Это относится и ко всей системе плоскостей, параллельных данной. Поэтому каждый дифракционный луч может рассматриваться как “отраженный” от системы параллельных атомных сеток – плоскостей. Сфера Эвальда в этом случае позволяет выделить в кристалле отражающие плоскости, которые сопоставляются узлам, лежащим на поверхности сферы.

2.7. Соотношение Вульфа–Брегга

Для определения углов, при которых возможны отражения рентгеновских лучей, рассмотрим систему кристаллографических плоскостей с расстоянием между ними равным d, т.е. представим кристалл как систему атомных плоскостей (рис.2.12).

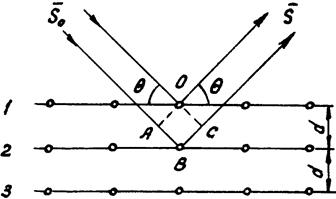
Рис. 2.12. К выводу уравнения Вульфа–Брегга.

Пусть падающий луч идет по направлению S₀ и составляет угол q с плоскостью (hkl), а отраженный дифракционный луч идет по направлениюSтакже под углом q к плоскости (hkl). Рассмотрим интерференцию отраженных волн от семейства параллельных плоскостей 1, 2, 3... с индексами (hkl). Рентгеновские лучи, проникая вглубь кристалла, будут отражаться не только от внешней 1-ой но и от внутренних 2, 3 и т.д. плоскостей. Отраженные от различных плоскостей лучи будут интерферировать между собой и усиливать друг друга, если разность хода лучей равна целому числу волн nl. Эту разность хода легко вычислить из рисунка 2.12. Она равна AB + BC = 2AB = 2d sinq. Посколькув направлении мы должны наблюдать луч дифракции, соответствующий максимуму интерференции, то

2d sinq = nl , (2.32)

где d – межплоскостное расстояние, n=1, 2, 3....

Это и есть формула Вульфа–Брегга. Угол q, входящий в нее, обычно называют углом скольжения или углом отражения; целое число n – порядком отражения.

Формула Вульфа–Брегга указывает на селективность (избирательность) появления отраженных рентгеновских лучей. В этом заключается отличие между отражением рентгеновских лучей от атомных плоскостей кристалла и отражением света от зеркала. Если для оптических лучей непрерывно менять угол между зеркалом и падающим лучом, то отраженный луч будет очень мало менять свою интенсивность. Для рентгеновских же лучей кривая интенсивности является кривой с резко выраженными максимумами. При этом условие дифракции выполняется только в том случае, когда

nl/2d = sinq £ 1 и nl£2d . (2.33)

Индексы интерференций.В формуле Вульфа–Брегга число n, называемое порядком отражения, показывает, какое число длин волн составляет разность хода падающих и отраженных лучей.

Преобразуем уравнение Вульфа–Брегга (2.32) и, разделив обе части его на n, получим

2(d_hkl / n) sinq = l . (2.34)

В этой формуле множитель d_hkl / n можно рассматривать, как межплоскостное расстояние новой системы (HKL) плоскостей. Эти плоскости реально могут и не существовать, но они должны удовлетворять условию:

d_hkl / n=d_HKL, (2.35)

где H, K, L – индексы фиктивной плоскости.

Индексы плоскости, как известно, обратно пропорциональны отрезкам, отсекаемым на осях координат и, следовательно, обратно пропорциональны межплоскостному расстоянию. Используя коэффициент пропорциональности p, запишем h=1/pa=1/pd_hkl

H= 1/pd_HKL=n/d_hkl или H= nh.

Индексы H, K, L новой системы плоскостей называются индексами интерференции. Для системы (HKL) уравнение Вульфа–Брегга запишем как:

2d_HKL×sinq=l . (2.37)

В последнем виде формула очень часто используется при индицировании рентгенограмм. Индексы интерференции используются при обозначении рефлексов на рентгенограммах.

Пользуясь соотношением (2.37), всегда следует помнить, что межплоскостное расстояние в этой формуле может отвечать некоторой фиктивной плоскости (HKL), индексы которой (индексы интерференции) всегда имеют общий множитель n. Реально же отражение происходит от плоскостей с индексами в n раз меньше и при разности хода в n раз больше.

Например, пусть разность хода между плоскостями (001) с межплоскостным расстоянием d₀₀₁ равна 4l. Тогда 2d₀₀₁×sinq=4l или (2d₀₀₁/4)sinq=l. Заменяя индексы реальных плоскостей (001) индексами интерференции, получим d/4=d¢ и 2d₀₀₄×sinq=l, где d¢=d₀₀₄. Таким образом, отражение от плоскости (001) с разностью хода, равной 4l, можно рассматривать условно как отражение от плоскости с индексами (004) и разностью хода l. Индексы содержат общий множитель, равный 4.