ЛЕКЦИЯ III. Рентгеноструктурный анализ. Метод Дебая.

Ранее, при рассмотрении дифракции рентгеновских лучей в кристаллах, отмечалось, что, если на неподвижный монокристалл направить пучок монохроматических рентгеновских лучей, то в общем случае ни один из узлов обратной решетки может не оказаться на сфере отражения, и, следовательно, дифракционных пятен на рентгенограмме мы не получим. Поэтому для получения отражения необходимо использовать либо сплошной рентгеновский спектр, либо непрерывно менять ориентацию кристалла по отношению к пучку. С этих позиций к основным методам рентгеноструктурного анализа относятся: 1) метод Дебая–Шеррера, 2) метод Лауэ, 3) метод вращения монокристаллов.

Сплошной рентгеновский спектр используется в методе Лауэ, изменение ориентации монокристалла и монохроматическое излучение – в методе вращения. В методе Дебая–Шеррера вместо того, чтобы изменять ориентацию одного единственного монокристалла, направляют пучок монохроматических лучей на поликристаллический образец – конгломерат беспорядочно ориентированных мелких кристалликов. Если кристаллики, из которых состоит образец, достаточно малы (5×10^-5–2×10^-4 см), то в просвечиваемом объеме их оказываются десятки миллионов. Следовательно, имеются любые их ориентации по отношению к лучу.

Поскольку большинство исследуемых образцов являются поликристаллами (ими являются, например, все металлы, поликристаллические тонкие слои полупроводников и др.), то мы и начнем более подробное рассмотрение рентгеноструктурного анализа с метода Дебая–Шеррера.

3.1. Исследование поликристаллических веществ методом Дебая–Шеррера

Типичная дебаеграмма, полученная в результате дифракции рентгеновских лучей в кристалле, представлена рядом колец (рис.3.1). Объяснение геометрии такой дифракционной картины можно дать на основе построения обратной решетки кристалла и сферы отражений.

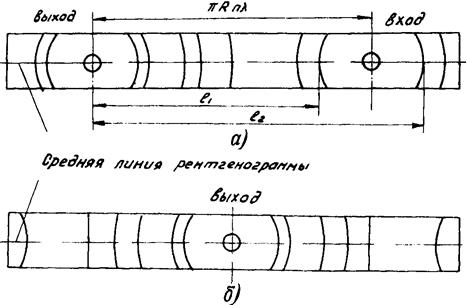
Рис.3.1.Схема асимметричной (а) и симметричной (б) рентгенограммы.

Построение дифракционной картины и геометрия съемки в камере РКД.Для построения дифракционной картины рассмотрим отражение рентгеновских лучей с длиной волны l последовательно для всех систем параллельных плоскостей поликристалла. Одну из таких систем обозначим (H₁K₁L₁) и определим для нее направление отраженного пучка. Поскольку бесчисленное множество кристалликов ориентировано в образце различно, то всегда найдется такой, для которого выполняется условие Вульфа–Брегга:

2dsinq₁ = l (3.1)

В обратной решетке эта система плоскостей обозначится узлом [[H₁K₁L₁]], а соответствующий ей вектор H₁ (рис.3.2) запишется как

H₁ = H₁a*+K₁b*+L₁c* (3.2)

Из последнего соотношения следует, что у данной системы плоскостей векторH₁ величина постоянная. Построим обратную решетку для одного из бесконечного множества кристаллов исследуемого поликристаллического образца. Выберем в качестве начала координат точку 0. Поскольку узел [[H₁K₁L₁]] отвечает условию отражения при угле q₁, то через него должна проходить сфера отражений. Построим эту сферу Эвальда (3.2).

Рассмотрим далее, как будет меняться положение вектора H₁ в поликристаллическом образце с бесконечным множеством различно ориентированных кристаллов. Для каждого отдельного кристаллика такого образца мы должны строить свою обратную решетку, так что мы получим бесчисленное множество обратных решеток. Все они будут равны по размерам (т.к. кристаллы одни и те же), но различно ориентированы в пространстве. Началом координат всех таких решеток является точка 0. Это равносильно тому, что обратная решетка как бы вращается вокруг центра 0.

Не рассматривая вращение всей решетки, проследим, как будет вести себя при этом вектор H₁. Он, очевидно, будет вращаться вокруг точки 0 таким образом, что конец его должен описать шаровую поверхность. Такая шаровая поверхность (покажем ее пунктиром на рис.3.2) будет включать в себя все узлы обратных решеток с индексами [[H₁K₁L₁]], соответствующие возможным ориентациям плоскостей (h₁k₁l₁) в пространстве.

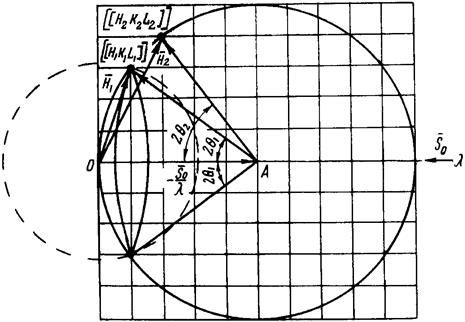
Рис.3.2. Построение дифракционной картины при съемке по методу Дебая.

Вернемся теперь к сфере Эвальда. Если мы хотим рассмотреть, как пойдут отраженные от плоскостей (H₁K₁L₁) лучи, то нужно выделить положение тех узлов, которые соответствуют величине вектораH₁, и в то же время попадают на сферу Эвальда. Очевидно это те узлы [[H₁K₁L₁]], которые лежат на линии пересечения сферы, показанной пунктиром, и сферы Эвальда. Поскольку число ориентаций кристалликов в пространстве бесчисленное множество, то и на окружности пересечения также будет бесчисленное множество узлов, соответствующих одной величине вектораH₁. Поэтому вектора S, проведенные из центра сферы Эвальда в эти точки и определяющие направление отраженных лучей, образуют непрерывную коническую поверхность с углом при вершине 4q₁. Следовательно, монохроматические лучи при съемке поликристалла должны отразиться от плоскостей (H₁K₁L₁) при q = q₁ по сплошной конической поверхности. Понятно, что не все кристаллики участвуют в этом отражении, а только те, плоскости (H₁K₁L₁) которых повернуты под углом q₁ к лучу.

Для следующего угла скольжения q = q₂ мы получим коническую поверхность, описанную вектором H_2,, проведенным в узел [[H₂K₂L₂]]. Можно получить конуса дифракции и для этой системы отражающих плоскостей. Угол при вершине этого конуса 4q₂. Рассуждая аналогично, получим при взаимодействии монохроматических рентгеновских лучей с поликристаллическим образцом серию дифракционных конусов.

Если на пути таких дифракционных конусов поместить цилиндрическую фотопленку, то на ней зарегистрируются попарно-симметричные дуги – кривые пересечения интерференционных конусов с цилиндрической поверхностью пленки (рис.3.1).

Обычно съемку осуществляют в цилиндрических камерах типа РКД (камера для рентгеноструктурного анализа по методу Дебая). Рентгеновская пленка в ней располагается по внутренней цилиндрической поверхности камеры. При съемке образца в цилиндрической кассете рентгенопленку располагают либо так, чтобы ее концы сходились у входного (для первичного пучка лучей) отверстия камеры М^// (рис.3.3,а). Это симметричная прямая съемка. Либо концы рентгенопленки сходятся у одного из концов диаметра, перпендикулярного лучу, как показано на рис.3.3,б. Это асимметричная съемка. При первом способе съемки получают симметричную рентгенограмму (рис.3.1,б), при втором – асимметричную (рис.3.1,а).

Расстояния между средними точками колец рентгенограмм пропорциональны соответствующим углам скольжения (рис.3.3). Действительно, дуга окружности длиной АВ=2l связана с измеренным в радианах углом при вершине конуса 4q соотношением

4q_рад=2l/R; q_рад=l/2R , (3.3)

где R – радиус цилиндрической рентгенопленки.

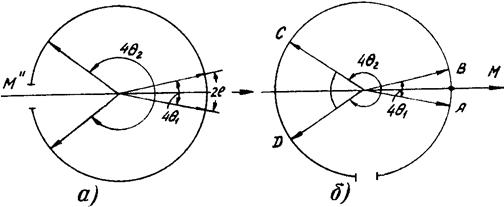
Рис.3.3. Геометрия съемки в дебаевской камере.

При угле q, измеренном в градусах

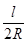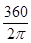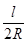q°= × =57,3 (3.4)

Если диаметр цилиндрической кассеты 2R взять равным 57,3 мм, то приближенно получим

q » l мм (3.5)

Таким образом, выраженный в градусах угол q будет равен половине расстояния между симметричными линиями рентгенограммы в мм.

При обоих способах съемки, симметричной и асимметричной, для расчета q требуется промерить расстояние l от выхода рентгеновского пучка (рис.3.3) до соответствующего кольца рентгенограммы. По ассиметричному снимку можно, кроме того, точно рассчитать радиус свернутой фотопленки и, следовательно, с большой точностью вычислить для каждой интерференционной линии угол скольжения

q = 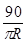× l (3.6)

Очевидно, что расстояние по окружности между осями симметрии, расположенными у входного и выходного отверстий равно pR (рис.3.3). Тогда для любой пары линий, например C и D, относящихся к одному и тому же конусу дифракции у входного отверстия

pR=(l₁+l₂)/2 , (3.7)

где l₁ и l₂ – расстояние этих линий от оси симметрии М у выходного отверстия. При подсчете радиуса пленки берут несколько таких пар линий у входа, рассчитывают по каждой паре pR и определяют затем среднее значение этой величины.

При симметричном способе съемки рассчитать радиус свернутой фотопленки по снимку невозможно и его либо приравнивают к радиусу камеры, либо ведут съемку с эталоном.

Порядок расположения и возможное число линий на дебаеграммах. Каждая линия на рентгенограмме получается в результате отражения рентгеновских лучей от какой-либо системы параллельных атомных плоскостей (HKL), так что индексы линий HKL на рентгенограмме совпадают с индексами отражающих плоскостей.

При съемке поликристаллического неподвижного образца в монохроматическом излучении положение линий на пленке-рентгенограмме определяется углом скольжения q. Определив угол скольжения q, можно сопоставить данную линию рентгенограммы системе плоскостей (HKL), или найти ее индексы интерференции. Например, для кубической решетки зависимость между индексами интерференций линии HKL и углом скольжения q определяется из сопоставления двух уравнений:

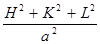= и l=2d_HKL× sinq

откуда sinq= 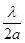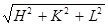, (3.8)

где a – период решетки, d – межплоскостное расстояние системы плоскостей (HKL), HKL – индексы интерференции линий.

Из уравнения (3.8) следует, что чем больше сумма квадратов индексов (H²+K²+L²) линий, тем больше угол отражения q. Следовательно, на рентгенограмме интерференционные линии будут располагаться в порядке возрастания суммы квадратов индексов отражающих плоскостей. Исходя из этого, можно составить таблицу, показывающую очередность расположения интерференционных линий на рентгенограмме поликристалла (табл.3.1).

Пользуясь соотношением (3.8), легко также установить максимально возможное число интерференционных линий на рентгенограмме. В силу того, что правая часть уравнения (3.8) не может быть больше 1 – на рентгенограмме должны появиться лишь те линии, для которых

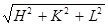£ (3.9)

Таблица 3.1

Последовательность расположения линий на дебаеграмме

Из этого неравенства вытекает, что общее количество линий на рентгенограмме определяется длиной волны рентгеновских лучей, а также размерами и формой элементарной ячейки. Чем жестче излучение (меньше l), тем больше линий появится на снимке.

Например, в кубической решетке при a = 2Å и l = 1,54Å имеем 2a/l=4/1,54»2,59 и H²+K²+L²£2,59²£7. Т.е., согласно табл. 3.1, максимально может появиться 6 линий, а с учетом погасаний – еще меньше. Последнее связано с тем, что в природе не существует структур с примитивной ячейкой. Реальные кристаллы имеют элементарные ячейки, в которых атомы располагаются не только по вершинам, но и внутри, а также на боковых гранях ячейки. В этих условиях относительная интенсивность рентгеновских лучей, отраженных от какой-либо плоскости (HKL), будет определяться структурной амплитудой F. Некоторые линии, для которых F=0, на рентгенограммах исчезают.