Четвертая функция сложного процента

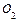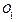Настоящая функция позволяет вычислить текущую стоимость будущей денежной суммы с учетом ставки процента i и темпа инфляции h. Пусть накопление денежной суммы в банке на дату составляет величину Определить ее стоимость на дату с учетом h и i. В данном случае необходимо выполнить дисконтирование по темпу инфляции и ставке процента.

Дисконтирование по h дает сумму

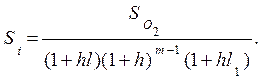(6.19)

Теперь эту сумму необходимо дисконтировать по i. В результате получим

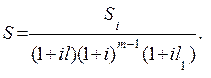(6.20)

Таким образом, S является текущей стоимостью накоплений в банке

Пример 6.4.Определить на 1 июня 2000 года стоимость накопления к 1 июня 2003 года суммы в 16400 рубля при темпе инфляции 10% и банковской ставке 3%.

Решение:В соответствии с (6.19) находим

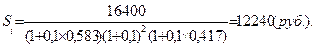
Далее в соответствии с (6.20)

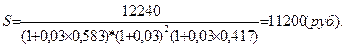
Сумма в 11200 рублей является той суммой, которую необходимо положить в банк 1 июня 2000 года для получения накопления при данной ставке процента и отсутствии инфляции в 12240 рублей к 1 июня 2003 года.

Пример 6.5.Решим задачу со спекулянтом из примера 1.4. Им будет продаваться земельный участок площадью 100 га по цене 3 млн.руб. за га, т.е. весь участок за 300 млн.руб. Дата продажи – 1 июня 2003 года. Какую цену он должен уплатить за этот участок 1 июня 2003 года, чтобы иметь ежегодный накапливаемый доход 12% при темпе инфляции в 10%.

Решение:

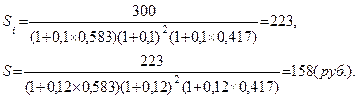
Таким образом при отсутствии инфляции сумма в 158 млн.руб. при 12% накоплений к концу срока приносит доход в 223 млн.руб., что соответствует с учетом инфляции сумме в 300 млн.руб.