СТОИМОСТЬ АКТИВА И ЗЕМЛИ ПРИ ОГРАНИЧЕННОЙ ВО ВРЕМЕНИ ИНФЛЯЦИИ
Пусть инфляция с постоянным темпов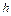 
ограничена периодом 
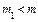(рис. 6.2)
Рис. 6.2.
Формула стоимости объекта здесь также имеет вид
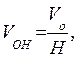(6.55)
где
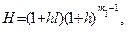
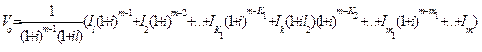(6.56)
Выполняя в (6.56) деление на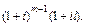 
Запишем
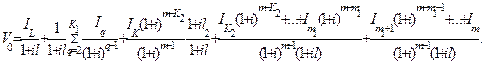(6.57)
Рассмотрим следующую сумму в (6.57)
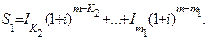
Допуская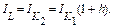 
Найдем
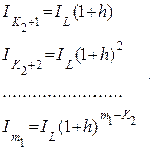
Запишем
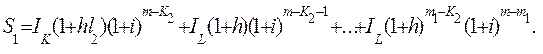
Выделим отсюда следующую составляющую
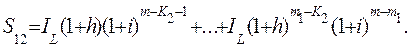
Разделив это выражение на величину
, 
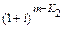получим
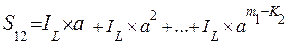
где
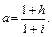
Поскольку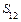 
является суммой членов геометрической прогрессии, в которой знаменатель
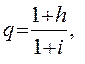
то очевидно, что
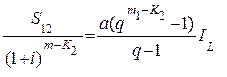
и тогда
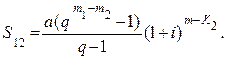
Сумма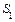 
тогда будет
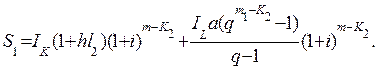(6.58)
Найдем теперь сумму
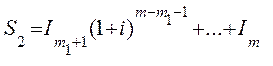
выражение (6.57).
Поскольку эта сумма соответствует безинфляционному накоплению, то положим
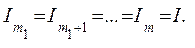
Сумма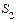 
является также суммой членов геометрической прогрессии с первым членом, равным единице и знаменателем
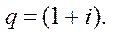
Тогда
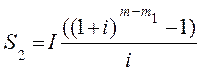(6.59)
С учетом (6.58) и (6.59) перепишем выражение (6.57)
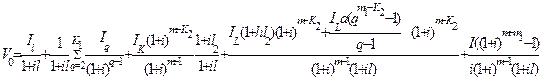(6.60)
Полагая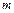 
стремящимся к бесконечности после выполнения делений в третьем, четвертом и пятом слагаемых формулы (6.60) найдем
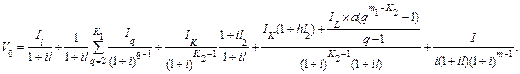(6.61)
При определенном, таким образом, значении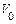 
находится стоимость земли в соответствии с (6.55).
Пример 6.1.Оценить стоимость земельного участка на 6 августа 2003 года. Участок будет продан 10 июля 2007 года. Темп инфляции до начала 2009 года составит величину 0,20 в год. Чистый операционный доход за период с момента оценки до конца года составил 20 у.е.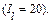 
На конец каждого последующего года чистый операционный доход составляет:
на 2005 – 100 у.е.
на 2006 – 120 у.е.
на 2007 – 144 у.е.
На момент продажи чистый операционный доход составит величину 70 у.е.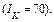 
Процентная ставка на капитал, вкладываемый в землю, равна 0,20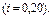 
Решение:Стоимость земельного участка определяется в соответствии с (6.55) по формуле
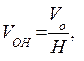
где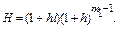 
Рис.6.3.
Выразим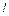 
в единицах года. Поскольку 6 августа – это 8,25 месяца, то
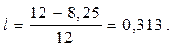
В данном случае
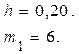
Найдем
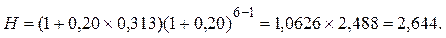
Для удобства расчетов снова перепишем формулу (6.61)
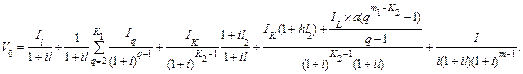
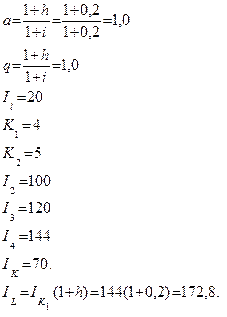
Поскольку после даты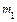 
темп инфляции равен нулю, то чистый операционный доход будет одинаковым. Примем его равным моменту 
.
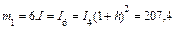Полагая 10 июля равным 6,33 месяца найдем
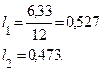
Таким образом, получим
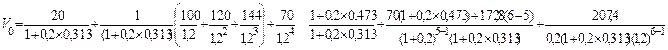
Замечание: В данном примере, поскольку q=1, принято
Дата добавления: 2016-02-02; просмотров: 599;