Шестая функция сложного процента
Пусть необходимо рассчитать взнос на амортизацию кредита, возвращаемого с учетом инфляции и процентной ставки.
Сумма возвращаемого кредита при определенных h и i равна
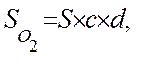 (6.24)
(6.24)
где c и d – те же, что и (6.22), (6.23).
Для амортизации, т.е. для компенсации кредита необходимо выплачивать 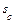 и
и 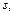 с тем чтобы накопление составило величину, равную (6.24). Тогда должно быть справедливым равенство
с тем чтобы накопление составило величину, равную (6.24). Тогда должно быть справедливым равенство
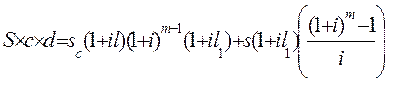 (6.25)
(6.25)
Правая часть (6.25) является следствием (6.15) при h=0.
Обозначим
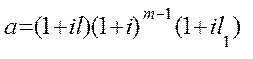 (6.26)
(6.26)
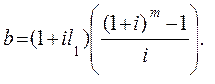 (6.27)
(6.27)
Величины (6.26) и (6.27) являются частными аналогами a и b в (6.17) при h=0.
С учетом этих обозначений запишем
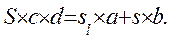 (6.28)
(6.28)
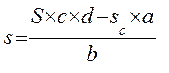 (6.29)
(6.29)
является взносом на амортизацию кредита.
Пример 6.7.1 июня 2000 года взят кредит в сумме 158 млн.руб. при темпе инфляции 10% и процентной ставке 3%. Кредит необходимо выплатить к 1 июня 2003 года. Первоначальный взнос на погашение кредита на дату 1 июня 2000 года (рис. 6.1) составил 10 млн.руб. Найти авансовый годовой взнос s на амортизацию кредита.
Решение:h=0,1, i=0,03. В соответствии с формулами (6.22), (6.23) найдем
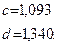
В соответствии с (6.26)
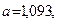
а в соответствии с (6.27)
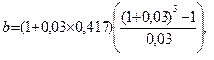
или
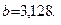
Тогда взнос s на амортизацию составит
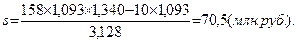
Дата добавления: 2016-02-02; просмотров: 640;
