Первая функция сложного процента

Пусть на дату 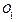вкладывается сумма 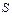до даты 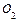(рис. 6.1)

Рис. 6.1

Число целых периодов между этими датами 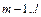и - промежутки времени между точкам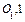и и 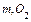соответственно.

Накопление в течение периода 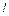составляет

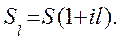(6.5)

С учетом индекса цен и соответственно покупательной стоимости

(6.6)

или

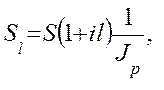(6.7)

где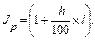

В течение оставшихся 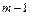периодов накопление составит

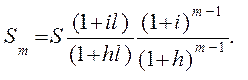(6.8)

В (6.8) и в дальнейшем темп инфляции выражен в сотых. За период 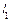накопление будет

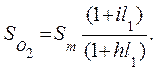(6.9)

Общая формула накопления будет

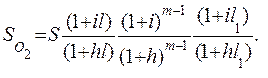(6.10)

При h=0

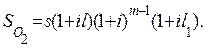(6.11)

Это есть накопление суммы 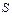за период между датам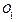и и 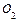при отсутствии инфляции. При 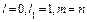(6.11) эквивалентна (1.1).

Пример 6.1.1 июня 2000 года 1500 рублей, т.е. 50 у.е. положены в сбербанк под 3% годовых. Темп инфляции рубля 10% в год. Определить сумму накопления на 1 июня 2003 года в рублях и в условных единицах.

Решение:В примере 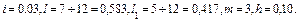В соответствии с формулой (6.10) найдем

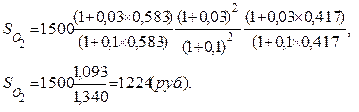
Поскольку банк не осуществляет компенсацию за инфляцию, то выдаваемая им клиенту сумма в срок 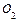равна

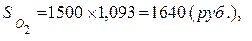
но при темпе инфляции в 10% покупательная способность денег составит величину

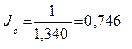
и сумма в 1640 рублей будет эквивалентна на 1 июня 2000 года сумме

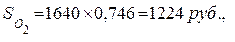
против суммы 1500 рублей. При данном темпе инфляции и ставке процента такое накопление явно убыточное.