Анализ инвестиций в реальные активы. Акционерное общество эмитировало:
ЗАДАЧА 16
Акционерное общество эмитировало:
1) обыкновенные акции нарицательной стоимостью 10 тыс. руб. в количестве 200 штук. Акции размещены с эмиссионным доходом (учитываемым в бухгалтерском учете как добавочный капитал) 3 тыс. руб. на акцию. Последний выплаченный дивиденд по акциям – 0,8 тыс. руб. Темп прироста дивидендов прогнозируется на уровне 2% в год;
2) привилегированные акции номиналом 1 тыс. руб., фиксированным размером дивиденда – 10% годовых, в количестве 500 штук. Акции размещены по цене 1,1 тыс. руб.
Нераспределенная прибыль по балансу – 5 500 тыс. руб.
Для финансирования приобретения внеоборотных активов привлечен кредит в размере 5 000 тыс. руб. под 17% годовых. Краткосрочный кредит в размере 500 тыс. руб. привлечен под 15% годовых. В расчетах считать, что проценты учитываются при налогообложении прибыли в пределах 15%, ставка налога на прибыль – 20%.
Руководство планирует выпуск облигаций нарицательной стоимостью 0,5 тыс. руб. со сроком погашения 5 лет и процентной ставкой 10% годовых на общую сумму 2 000 тыс. руб. Расходы по реализации облигаций составят в среднем 3% нарицательной стоимости. Облигации планируется продавать с дисконтом 2% номинала. Заем планируется привлечь для финансирования проекта с внутренней нормой рентабельности 15% годовых.
Рассчитать цену капитала до и после размещения облигаций.
Определить целесообразность привлечения облигационного займа для финансирования проекта.
Решение.
Рассчитаем «цену» отдельных видов капитала организации.
1. «Цена» обыкновенных акций (ЦОА) для случая, когда известен (или прогнозируется) постоянный темп прироста дивидендов определяется на основе модели Гордона:
ЦОА = C1 / PОА + g,
где C1 – прогнозное значение дивиденда на ближайший период;
PОА – текущая стоимость обыкновенной акции (в данном случае – это цена размещения);
g – прогнозный темп прироста дивидендов (в доле целого числа).
ЦОА = [0,8 × 1,02 / (10+3) + 0,02] × 100 = 8,28% годовых к сумме привлеченного капитала.
2. «Цена» привилегированных акций (ЦПА):
ЦПА = C / PПА,
где C – дивиденд (в денежных единицах);
PПА – текущая стоимость привилегированной акции (в данном случае – цена размещения).
ЦПА = (1×0,10 / 1,1)×100 = 9,09 % годовых к сумме привлеченного капитала.
3. «Цена» нераспределенной прибыли (ЦНП):
ЦНП = ЦОА = 8,28% годовых к сумме данного вида капитала.
4. «Цена» кредита (ЦК). Если проценты по кредиту не уменьшают налогооблагаемую прибыль, то цена кредита для организации-заемщика равна процентной ставке по нему:
ЦК = r,
где r – годовая процентная ставка по кредиту.
Если же проценты уменьшают налогооблагаемую прибыль, то создается «налоговый щит» и цена кредита для организации-заемщика оказывается меньше номинальной процентной ставки:
ЦК = r × (1-Сн),
где Сн – ставка налогообложения прибыли в долях единицы.
Таким образом, по первому кредиту:
ЦК = 15% × (1 - 0,2) + (17%-15%) = 14%
По второму:
ЦК = 15% × (1-0,2) = 12%
5. «Цена» облигационного займа (ЦОБЛ). Базовая формула для расчета имеет следующий вид:
ЦОБЛ = 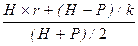 × 100,
× 100,
где Н – номинал облигации;
r – процентная ставка (в долях единицы);
P – текущая стоимость облигации (здесь: стоимость размещения).
Текущая (реализационная) стоимость облигации:
P = Н – сумма дисконта – расходы по реализации = 0,5-0,5×0,02-0,5×0,03 =
= 0,5 × (1-0,05) = 0,5 × 0,95 = 0,475 тыс. руб.
ЦОБЛ = [0,5×0,1 + (0,5-0,475)/5] / [(0,5+0,475)/2]×100 = 11,28 % годовых к сумме привлеченных средств.
Средняя «цена» («стоимость») капитала (WAСС) определяется по формуле средневзвешенной:
WAСС = 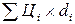 ,
,
где Цi – «цена» i-го источника;
di – доля i-го источника в общей сумме капитала.
Таблица 1
Расчет средней «цены» капитала без учета облигационного займа
| Источник финансирования | Учетная (балансовая) оценка | Доля (di) в общей сумме капитала | «Цена» отдельных видов капитала (Цi), % | Средневзвешенная «цена» капитала (СС), % | |
| Расчет | Величина, тыс. руб. | ||||
| 6 [4×5] | |||||
| Обыкновенные акции | (10+3)×200 | 2 600 | 0,184 | 8,28 | 1,52 |
| Привилегированные акции | 1,1×500 | 0,039 | 9,09 | 0,35 | |
| Нераспределенная прибыль | 5 500 | 0,389 | 8,28 | 3,22 | |
| Долгосрочный кредит | 5 000 | 0,353 | 14,00 | 4,95 | |
| Краткосрочный кредит | 0,035 | 12,00 | 0,42 | ||
| Итого инвестированный капитал | х | 14 150 | 1,000 | х | 10,46 |
Таблица 2
Расчет средней «цены» капитала с учетом облигационного займа
| Источник финансирования | Учетная (балансовая) оценка | Доля (di) в общей сумме капитала | «Цена» отдельных видов капитала (Цi), % | Средневзвешенная «цена» капитала (СС), % | |
| Расчет | Величина, тыс. руб. | ||||
| 6 [4×5] | |||||
| Обыкновенные акции | (10+3)×200 | 2 600 | 0,162 | 8,28 | 1,34 |
| Привилегированные акции | 1,1×500 | 0,034 | 9,09 | 0,31 | |
| Нераспределенная прибыль | 5 500 | 0,343 | 8,28 | 2,84 | |
| Долгосрочный кредит | 5 000 | 0,312 | 14,00 | 4,36 | |
| Краткосрочный кредит | 0,031 | 12,00 | 0,37 | ||
| Облигационный заем | 2000×(1-0,02-0,03) | 1 900 | 0,118 | 11,28 | 1,34 |
| Итого инвестированный капитал | х | 16 050 | 1,000 | х | 10,56 |
Средняя «цена» капитала организации до привлечения облигационного займа составляет 10,46%. С размещением облигаций «цена» возрастет несущественно – до 10,56%. Причем, так как «цена» облигационного займа (11,28%) ниже внутренней рентабельности инвестиционного проекта, для финансирования которого и привлекается этот заем (15%), финансирование проекта за счет данного источника экономически целесообразно.
ЗАДАЧА 17
Оценить целесообразность приобретения новой технологической линии на основе следующих данных.
Величина вложений в основные средства – 20 000 тыс. руб. Срок эксплуатации – 10 лет. Износ начисляется линейным способом в течение срока эксплуатации. Прогноз выручки от продаж без НДС по годам:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 000 | 12 000 | 13 000 | 14 000 | 15 000 | 15 000 | 14 000 | 14 000 | 13 000 | 12 000 |
Переменные затраты на производство и реализацию продукции – 50% выручки от продаж (в том числе сырье и материалы – 20%). Постоянные расходы (без учета амортизации) – 1 500 тыс. руб. Ставка налога на прибыль - 20%.
Сложившееся хозяйственно-финансовое положение таково, что коэффициент рентабельности инвестированного капитала составляет 18-20%; «цена» инвестированного капитала – 15%. Руководство не считает целесообразным участвовать в реализации проектов со сроком окупаемости более 5 лет.
Решение.
На первом этапе решения осуществляется расчет чистой прибыли и денежного потока по периодам реализации проекта (табл. 1).
Далее рассчитываются показатели, характеризующие эффективность проекта (табл. 2-4). Традиционными критериями оценки эффективности инвестиционных проектов являются: коэффициент эффективности инвестиций (учетная норма прибыли - ARR); простой срок окупаемости (РР); чистая текущая (приведенная) стоимость (NPV); индекс рентабельности инвестиций (IP); внутренняя норма прибыли (IRR).
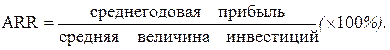
Так как в течение всего срока эксплуатации проекта денежные притоки варьируют, срок окупаемости (РР) будет рассчитан прямым подсчетом числа лет, в течение которых поступления по проекту покроют первоначальные инвестиции:
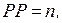 при котором
при котором 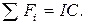
Расчет срока окупаемости выполнен следующим образом. Кумулятивный денежный приток превысит величину инвестиций через 5 лет (22000 >20000). Если округлять срок окупаемости до целых лет, он составляет 5 лет. Если ввести предположение о равномерном внутригодовом распределении денежного потока, можно исчислить дробную часть года пятого года:
превышение первоначальной инвестиции над кумулятивным денежным притоком полных лет срока окупаемости (в данном случае четырех) / денежный приток последнего года срока окупаемости (в данном случае пятого) = (20 000 – 16 800) / 5 200 = 0,62 года или около 8 месяцев (0,62 × 12 мес.).
Таким образом, срок окупаемости составляет 4,62 года или около 4 лет 8 месяцев.
Чистая текущая стоимость проекта трактуется как разность между настоящей стоимостью всех будущих поступлений и стоимостью единовременных первоначальных инвестиций:
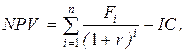
где NPV – чистая текущая стоимость;
Fi –ежегодные поступления;
IC – первоначальные инвестиции (единовременные затраты);
r – коэффициент дисконтирования (ставка доходности по альтернативным вложениям, среднеотраслевая норма прибыли либо норма прибыли, требуемая инвестором);
n – срок реализации проекта (лет).
Разновидностью метода чистой текущей стоимости является расчет индекса рентабельности инвестиций по формуле:
Таблица 1
Расчет чистой прибыли и денежного потока по периодам реализации проекта
| Показатели | Период (годы) | Итого | |||||||||
| 1. Выручка от продаж (без НДС) | |||||||||||
| 2. Переменные затраты на производство и реализацию продукции (стр.1 × 0,5) | |||||||||||
| 3. Постоянные затраты (без учета амортизации) | |||||||||||
| 4. Амортизация | |||||||||||
| 5. Прибыль до налогообложения (стр.1 - стр.2 - стр.3 - стр.4) | |||||||||||
| 6. Налог на прибыль (стр.5 × 0,20) | |||||||||||
| 7. Чистая прибыль (стр.5 - стр.6) | |||||||||||
| 8. Денежный приток от текущей деятельности (стр.7 + стр.4) | |||||||||||
| 9. Кумулятивный денежный приток от текущей деятельности (для расчета срока окупаемости) | х |
Таблица 2
Расчет чистой текущей стоимости проекта при цене капитала (коэффициенте дисконтирования) 15%
| Показатели | Период (годы) | Итого | ||||||||||
| 1. Инвестиции | х | х | х | х | х | х | х | х | х | х | ||
| 2. Чистый денежный приток | - | х | ||||||||||
| 3. Дисконтирующий множитель FM2(15%; i) | 1,000 | 0,870 | 0,756 | 0,658 | 0,572 | 0,497 | 0,432 | 0,376 | 0,327 | 0,284 | 0,247 | х |
| 4. Текущая стоимость инвестиций (стр.1 × стр.3) | х | х | х | х | х | х | х | х | х | х | ||
| 1. Текущая стоимость денежного притока (стр.2 × стр.3) | - | |||||||||||
| 5. Чистая текущая стоимость, тыс. руб. [стр.5 - стр.4] | х | х | х | х | х | х | х | х | х | х | х |
Таблица 3
Расчет чистой приведенной стоимости проекта при коэффициенте дисконтирования 20%
| Показатели | Период (годы) | Итого | ||||||||||
| 1. Инвестиции | х | х | х | х | х | х | х | х | х | х | ||
| 2. Чистый денежный приток | - | х | ||||||||||
| 3. Дисконтирующий множитель FM2(15%; i) | 1,000 | 0,833 | 0,694 | 0,579 | 0,482 | 0,402 | 0,335 | 0,279 | 0,233 | 0,194 | 0,162 | х |
| 4. Текущая стоимость инвестиций (стр.1 × стр.3) | х | х | х | х | х | х | х | х | х | х | ||
| 2. Текущая стоимость денежного притока (стр.2 × стр.3) | - | |||||||||||
| 5. Чистая текущая стоимость, тыс. руб. [стр.5 - стр.4] | х | х | х | х | х | х | х | х | х | х | х | -1572 |
Таблица 4
Расчет показателей экономической эффективности реализации
инвестиционного проекта
| Показатели | Расчет | Величина |
| Коэффициент эффективности инвестиций, % | (25 200 / 10) × 100 0,5 × 20 000 | 25,2 |
| Срок окупаемости проекта, лет | Число полных лет = 4, т.к. кумулятивный денежный приток по текущей деятельности за 5 лет 22 000 > 20 000. Дробная часть пятого года = (20 000 – 16 800) / 5 200 = 0,62 | 4,62 |
| Чистая текущая стоимость, тыс. руб. | 22 240 – 20 000 | 2 240 |
| Индекс рентабельности инвестиций | 22 240 / 20 000 | 1,112 |
| Внутренняя норма рентабельности, % | 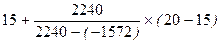
| 17,9 |
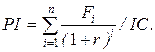
Значение IRR находят при помощи функции Microsoft Excel. Далее для расчета IRR используют следующую формулу:
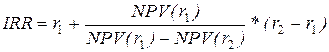
Таким образом, для исчисления внутренней нормы рентабельности инвестиций следует рассчитать чистую текущую стоимость проекта при измененном в сторону увеличения коэффициенте дисконтирования, таким образом, чтобы чистая текущая стоимость имела отрицательное значение (например, 20%) (таблица 3).
Внутренняя норма рентабельности инвестиций, рассчитанная без учета выплат инвесторам (кредиторам), характеризует максимально допустимую цену капитала, используемого для финансирования проекта.
Далее сформируем экономическую оценку полученных значений критериев.
Коэффициент эффективности инвестиционного проекта (учетная норма рентабельности) составляет 25,2% при рентабельности капитала, инвестированного в деятельность, которой занимается организация, на уровне 18-20%. То есть проект обеспечивает более высокую норму рентабельности на инвестиции в учетных (недисконтированных) оценках и, согласно рассматриваемому критерию, является выгодным.
Срок окупаемости проекта составляет 4,62 года, при этом руководство организации не считает целесообразным участвовать в реализации проектов со сроком окупаемости более 5 лет. Таким образом, по данному критерию реализация проекта является целесообразной.
Чистая текущая (приведенная) стоимость проекта (2 240 тыс. руб.) больше нуля. Это означает, что текущая стоимость будущих поступлений от реализации проекта больше текущей стоимости инвестиционных вложений в него, следовательно, проект является выгодным. Поскольку чистая приведенная стоимость больше нуля, индекс рентабельности инвестиций выше 1,0.
Внутренняя норма рентабельности инвестиций имеет значение, равное 17,9% при ныне существующей «цене» капитала 15%, что создает определенный «запас» прочности проекта, связанный с тем, что до тех пор, пока «цена» капитала не поднимется выше 17,9%, проект будет приносить прибыль даже с учетом необходимости ежегодных выплат владельцам привлеченного капитала. Таким образом, если значительный риск повышения цены капитала до уровня выше 17,9 % отсутствует, проект является экономически эффективным.
Задача 18
Ожидаемые поступления от проекта:
с 1 по 5 годы – по 2 000 тыс. руб. ежегодно;
с 6 по 10 годы – по 2 500 тыс. руб. ежегодно;
с 11 по 20 годы – по 1 800 тыс. руб. ежегодно.
Сумма инвестиционных вложений составляет 19 000 тыс. руб. Найти суммарную приведенную стоимость денежных поступлений за 20 лет и чистую приведенную стоимость при альтернативной стоимости капитала 10%.
Решение.
В данном случае денежные потоки представляют собой аннуитеты. Для упрощения решения целесообразно воспользоваться дисконтирующими множителями для аннуитетов:
FM 4 (10%;5) = 3,791;
FM 4 (10%;10) = 6,145;
FM 4 (10%;20) = 8,514.
Тогда текущая (приведенная) стоимость денежного потока для периода с первого по пятый год:
P (1¸5) = 2 000×3,791 = 7 582 тыс. руб.
Для периода с 6 по 10 год:
P (6¸10) = 2 500× (6,145-3,791) = 5 885 тыс. руб.
Для периода с 11 по 20 год:
P (11¸20) = 1 800 × (8,514-6,145) = 4 264 тыс. руб.
Суммарная стоимость денежных поступлений:
P (1¸20) = P (1¸5) + P (6¸10) + P (11¸20) =
= 7 582 + 5 885 + 4 264 = 17 731 тыс. руб.
Величина инвестиционных вложений в проект (IC) составляет 19 000 тыс. руб., следовательно, проект имеет отрицательную чистую приведенную стоимость:
NPV = P (1¸20) – IC = 17 731-19 000 = - 1 269 тыс. руб.
и при альтернативной стоимости капитала, равной 10%, является экономически нецелесообразным.
Задача 19
Сравните, используя все известные критерии, два проекта, если цена капитала – 12%. Амортизация осуществляется линейным способом в течение срока действия проекта. Ликвидационная стоимость равна нулю. Влияние налогообложения прибыли не рассматривать.
| Проект | Денежные потоки по годам, тыс. руб. | |||||
| А | -1200 | |||||
| Б | -1200 |
Решение.
Таблица 1
Расчет показателей экономической эффективности
реализации инвестиционных проектов
| Показатели | Проект А | Проект Б | ||
| Расчет | Величина | Расчет | Величина | |
| 1. Коэффициент эффективности инвестиций, % | [(300+400+500+400+ 300-1200[15])/5] / [(1/2×(1200+0)] | 23,33 | [(500+400+350+300+ 200-1200)/5] / [(1/2×(1200+0)] | 18,33 |
| 2. Срок окупаемости, лет | 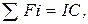 300+400+500 = 1200; Þ
300+400+500 = 1200; Þ 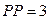
| 3,00 | 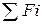 =500+400+350 > 1200
Þ PP=2 полных года и (1200-500-400)/350 дробная часть года =500+400+350 > 1200
Þ PP=2 полных года и (1200-500-400)/350 дробная часть года
| 2,86 |
Окончание табл.1
| Показатели | Проект А | Проект Б | ||
| Расчет | Величина | Расчет | Величина | |
| 3. Текущая (приведенная) стоимость денежных притоков, тыс. руб. | 300×0,893+400×0,797 500×0,712+400×0,636+300×0,567[16] | 500×0,893+400×0,797+350×0,712+300×0,636+200×0,567 | ||
| 4. Чистая текущая (приведенная) стоимость, тыс. руб. | 1367-1200 | 1319-1200 | ||
| 5. Индекс рентабельности инвестиций | 1367/1200 | 1,14 | 1319/1200 | 1,10 |
| 6. Внутренняя норма рентабельности, % | - | - | - | - |
| 6.1. Коэффициент дисконтирования, при котором NPV предположительно будет иметь отрицательное значение | 0,2 | 0,2 | ||
| 6.2. Чистая текущая (приведенная) стоимость проектов при данном коэффициенте дисконтирования | 300×0,833+400×0,694 +500×0,579+ 400× 0,482+300×0,402-1200 | -69,6 | 500×0,833+400×0,694+350×0,579+300×0,482+200×0,402-1200 | -78,3 |
| 6.3. Внутренняя норма рентабельности, % | 12+167/(167-(-69,6)) × (20-12) | 17,6 | 12+119/(119-(-78,3)) × (20-12) | 16,8 |
В соответствии со всеми рассчитанными критериями, кроме срока окупаемости, предпочтение отдается проекту А. При этом разница в сроках окупаемости не является значительной.
В случае, когда критерии дают противоположные оценки, следует учитывать следующее. Среди приемов, основанных на дисконтируемых и учетных оценках, предпочтение следует отдавать первой группе, т.к. они учитывают временную компоненту денежных потоков. При выборе из двух альтернативных проектов с одинаковыми первоначальными инвестициями предпочтение отдается критерию чистой приведенной стоимости. Индекс рентабельности в данном случае может не рассчитываться, т.к. при равных инвестиционных вложениях, при сравнении проектов он будет давать результат, идентичный критерию NPV. Внутренняя норма рентабельности (IRR) показывает лишь максимальную цену капитала, ассоциируемого с оцениваемыми проектами, поэтому, если нет значительного риска повышения цены капитала до уровня выше IRR, предпочтение следует отдавать проекту, приносящему больший NPV.
Задача 20
Проанализировать два альтернативных проекта, если цена капитала 10%.
| Проект | Денежные потоки по годам, тыс. руб. | |||
| А | -1000 | - | ||
| Б | -1000 |
Решение.
Число лет, в течение которых поступают доходы от реализации проектов неодинаково, поэтому расчет чистой текущей (приведенной) стоимости обычным способом не является корректным. Для анализа может использоваться один из нижеприведенных подходов.
1 вариант – метод наименьшего общего кратного.
Для обеспечения сопоставимости проекты рассматриваются как повторяющиеся. Наименьшее общее кратное – 6. В течение этого периода проект А будет повторен 3 раза (6/2), проект Б – 2 (6/3).
NPV проектов однократной реализации:
NPVА = 600/(1+0,1)1 +800/(1+0,1)2 – 1000
= 600×0,909 + 800×0,826 –1000 = 206 тыс. руб.
NPVБ = 450/(1+0,1)1 +700/(1+0,1)2 + 450/(1+0,1)3 – 1000 =
= 450×0,909 + 700×0,826 +450×0,751–1000 = 325 тыс. руб.
Суммарная чистая текущая (приведенная) стоимость повторяющегося потока:
NPV (i; n) = NPV(i) × (1+1/(1+r)i + 1/(1+r)2×i+ … ),
где NPV(i) – NPV исходного (повторяющегося) проекта;
i – продолжительность этого проекта;
r – коэффициент дисконтирования;
n – число повторений исходного проекта.
Суммарная чистая приведенная стоимость проекта А трехкратной реализации:
NPV(2;3) = 206 + 206/(1+0,1)2 + 206/(1+0,1)4 = 206 + 170 + 141 = 517 тыс. руб.
Или по вышеприведенной формуле
NPV(2;3) = 206 × (1+1/(1+0,1)2 + 1/(1+0,1)4) =
=206 × (1+0,826+0,683) = 517 тыс. руб.
Суммарная чистая приведенная стоимость проекта Б двухкратной реализации:
NPV(3;2) = 325 × (1+1/(1+0,1)3 ) = 325 × (1+0,751) = 569 тыс. руб.
Так как суммарная чистая текущая (приведенная) стоимость проекта Б больше, чем проекта А, первый из вышеназванных проектов предпочтительнее.
Для наглядности принцип решения отражен на рис. 1.
Проект А
| NPV | Денежные потоки по годам | ||||||
| -1000 | |||||||
| 206/(1+0,1)2 | -1000 | ||||||
| 206/(1+0,1)4 | -1000 | ||||||
| Итого: 206 + 206/(1+0,1)2 + 206/(1+0,1)4 = 206 × (1+1/(1+0,1)2 + 1/(1+0,1)4) = 517 |
Проект Б
| NPV | Денежные потоки по годам | ||||||
| -1000 | |||||||
| 325/(1+0,1)3 | -1000 | ||||||
| Итого: 325+325/(1+0,1)3 = 325×(1+1/(1+0,1)3) = 569 |
Рисунок 1 - Схема исчисления суммарной чистой приведенной стоимости при неоднократной реализации проектов
2 вариант – метод бесконечного повторения сравниваемых проектов.
NPV (i;¥) = 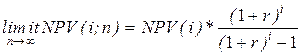
Проект А:
i = 2, NPV (2;¥) = 206 × 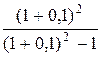 = 206 × 5,762 = 1 187 тыс. руб.
= 206 × 5,762 = 1 187 тыс. руб.
Проект Б:
i = 3, NPV (3;¥) = 325 × 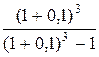 = 325 × 4,021 = 1 307 тыс. руб.
= 325 × 4,021 = 1 307 тыс. руб.
Чистая приведенная стоимость проекта Б при бесконечной реализации больше, чем проекта А, следовательно, проект Б экономически выгоднее.
Задача 21
Организация имеет возможность инвестировать:
А) до 800 тыс. руб., проекты поддаются дроблению (может быть профинансирована какая-то часть проекта, соответственно пропорционально изменятся доходы);
Б) до 650 тыс. руб., проекты дроблению не поддаются.
Цена капитала составляет 10%.
Требуется составить оптимальный инвестиционный портфель из нижеследующих проектов.
| Проект | Денежные потоки по годам, тыс. руб. | |||||
| А | -400 | |||||
| Б | -200 | |||||
| В | -300 | |||||
| Г | -150 | |||||
| Справочно: дисконтирующий множитель FM2(10%;i) | 1,000 | 0,909 | 0,826 | 0,751 | 0,683 | 0,621 |
Решение.
Оптимальный инвестиционный портфель составляется путем максимизации значения суммарной чистой приведенной стоимости проектов, включаемых в портфель.
Для случая поддающихся дроблению проектов максимизация суммарной NPV при заданном ограничении инвестиционных вложений достигается на основе включения в портфель проектов, имеющих наибольшее значение индекса рентабельности инвестиций. Для случая, когда проекты не поддаются дроблению максимальное значение суммарной чистой приведенной стоимости находится путем последовательного просмотра всех возможных вариантов сочетания проектов и расчетом суммарной NPV для каждого варианта.
На первом этапе решения рассчитывается NPV и индекс рентабельности для каждого проекта.
Таблица 1
Расчет чистой приведенной стоимости и индекса рентабельности
инвестиционных проектов
| Проект | Приведенная стоимость денежных притоков (PV) | Чистая приведенная стоимость (NPV) | Индекс рентабельности инвестиций (PI) | |||
| Расчет | Величина, тыс. руб. | Расчет | Величина, тыс. руб. | Расчет | Величина | |
| А | 100×0,909+150×0,826+200× 0,751+150×0,683+100×0,621 | 530-400 | 530/400 | 1,33 | ||
| Б | 60×0,909+70×0,826+80×0,751 + 90×0,683+100×0,622 | 296-200 | 296/200 | 1,48 | ||
| В | 90×0,909+90×0,826+90×0,751 + 90×0,683+90×0,623 | 341-300 | 341/300 | 1,14 | ||
| Г | 50×0,909+50×0,826+40×0,751 + 40×0,683+30×0,624 | 163-150 | 163/150 | 1,09 |
А) ограничение инвестиции - до 800 тыс. руб., проекты поддаются дроблению.
Таблица 2
Оптимальный портфель инвестиционных проектов, поддающихся
дроблению, при ограничении инвестиций размером 800 тыс. руб.
| Проект[17] | Индекс рентабельности инвестиций | Инвестиция, включаемая в портфель, тыс. руб. | Часть инвестиции, включаемой в портфель, % | Чистая приведенная стоимость, тыс. руб.[18] |
| Б | 1,48 | 100,00 | ||
| А | 1,33 | 100,00 | ||
| В | 1,14 | 66,67 | ||
| Г | 1,09 | 0,00 | ||
| Итого | х | Х |
Б) ограничение инвестиции - до 650 тыс. руб., проекты не поддаются дроблению.
Таблица 3
Возможные сочетания проектов, не поддающихся дроблению,
при ограничении инвестиций размером 650 тыс. руб.
| Вариант | Суммарная инвестиция, тыс. руб. | Суммарная чистая приведенная стоимость, тыс. руб. | ||
| Расчет | Величина | Расчет | Величина | |
| А+Б | 400+200 | 130+96 | ||
| А+Г | 400+150 | 130+13 | ||
| Б+В+Г | 200+300+150 | 96+41+13 |
Максимальную суммарную чистую приведенную стоимость имеет портфель, сочетающий проекты А и Б (226 тыс. руб.), таким образом, он и является оптимальным.
Дата добавления: 2016-02-02; просмотров: 1250;
