Финансовых вычислений. 1. Процесс, в котором заданы исходная сумма и процентная ставка, в финансовых вычислениях называется процессом:
1. Процесс, в котором заданы исходная сумма и процентная ставка, в финансовых вычислениях называется процессом:
а) дисконтирования;
б) оценки ценных бумаг;
в) наращения;
г) аннуитета.
2. Путем наращения определяется:
а) будущая стоимость капитала (вложений);
б) настоящая стоимость капитала (вложений);
в) дисконтирующий множитель;
г) степень изменения доходности отдельного фондового инструмента от изменения доходности рынка в целом.
3. Экономический смысл дисконтирования заключается в:
а) временном упорядочении денежных потоков различных временных периодов;
б) определении рискованности вложений;
в) определении будущей стоимости вложенных инвестиций;
г) вычислении эффективной процентной ставки.
4. Ставка процента (r) определяется по формуле (d - ставка дисконта; F - возвращаемая сумма с процентами; Р - вложенная сумма):
а) 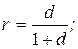
б) 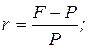
в) 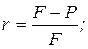
г) 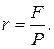
5. Инвестиция (Р) сделана на условиях простого процента, если размер инвестированного капитала через n лет (Fn):
а) 
б) 
в) 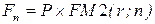
г) 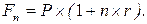
6. Инвестиция (Р) сделана на условиях сложного процента, если размер капитала через n лет равен (Fn ):
а) 
б) 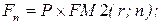
в) 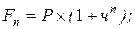
г) 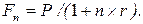
7. Множитель, показывающий, чему будет равна одна денежная единица через n периодов при заданной процентной ставке r:
а) факторный (мультиплицирующий) множитель 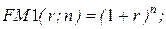
б) дисконтирующий множитель 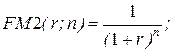
в) факторный (мультиплицирующий) множитель 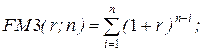
г) дисконтирующий множитель 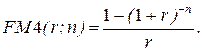
8. Формула сложных процентов с внутригодовыми начислениями (n - число лет; m - количество начислений в году):
а) 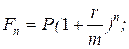
б) 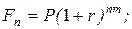
в) 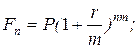
г) 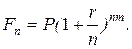
9. Чем чаще в году начисляются проценты по схеме сложных процентов, тем:
а) меньше итоговая накопленная сумма;
б) больше итоговая накопленная сумма;
в) накопленная сумма не меняется в зависимости от частоты начисления процентов;
г) выше риск вложений.
10. Больший рост банковского вклада за один и тот же период произойдет при применении
а) простых процентов;
б) сложных процентов.
11. Начисления 1 % в месяц по схеме сложных процентов:
а) равно 12% годовых;
б) меньше 12% годовых;
в) больше 12% годовых;
г) равно 24%.
12. За какой срок вклад в 100 тыс. руб. увеличится в два раза при ежегодном начислении простых процентов по ставке 10% ?
а) 2 года;
б) 3 года;
в) 5 лет;
г) 10 лет.
13. Определите сумму сложных процентов, начисленных к концу срока при инвестировании 200 тыс. руб. на 3 года под 7% годовых:
а) 14 тыс. руб.;
б) 42 тыс. руб.;
в) 45 тыс. руб.;
г) 242 тыс. руб.;
д) 245 тыс. руб.
14. Используя формулу сложных процентов определить сумму депозитного вклада в размере 50 тыс. руб. через 2 года при ежегодном начислении 9% годовых:
а) 9 тыс. руб.;
б) 9,4 тыс. руб.;
в) 50 тыс. руб.;
г) 59 тыс. руб.;
д) 59,4 тыс. руб.
15. Используя формулу простых процентов, определите сумму средств к погашению краткосрочного кредита в размере 20 млн руб. через 45 дней при годовой ставке 17%:
а) 0,42 млн руб.;
б) 3,40 млн руб.;
в) 20,00 млн руб.;
г) 20,42 млн руб.;
д) 23,40 млн руб.
16. Определите требуемый объем инвестиционного капитала, чтобы через 2 года его величина составила 50 млн руб. при годовой ставке доходности 15%, начисляемой по схеме сложных процентов:
а) 35 млн руб.;
б) 37,8 млн руб.
в) 38,5 млн руб.
г) 33,9 млн руб.
17. Определите размер вексельного кредита при учете векселя в сумме 500 тыс. руб. за 110 дней до наступления срока погашения (в расчете использовать календарное число дней в году - 365). Годовая ставка дисконта 18%:
а) 27,1 тыс. руб.;
б) 410,0 тыс. руб.;
в) 472,9 тыс. руб.;
г) 474,3 тыс. руб.;
д) 527,1 тыс. руб.
18. Приведенная (текущая) стоимость характеризует:
а) будущую стоимость денежного потока F1, F2 ... F3;
б) регулярные поступления от инвестиций;
в) стоимость денежного потока F1, F2 ... F3 с позиции текущего момента;
г) чему будет равна одна денежная единица через n периодов при заданной процентной ставке r.
19. Базовая формула для расчета текущей (приведенной) стоимости (Fn - доход, планируемый к получению в году n; r - коэффициент дисконтирования; Р - текущая стоимость планируемого дохода):
а) 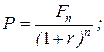
б) 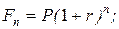
в) 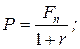
г) 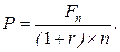
20. Величина приведенного денежного потока за n периодов (Fi - денежный приток (отток) в i-том году):
а) 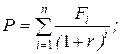
б) 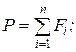
в) 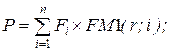
г) 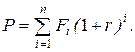
21. При годовом значении коэффициента дисконтирования 13 % доходы от инвестиций составили: в первый - 10 млн руб., во второй - 15 млн руб., в третий - 20 млн руб. Какова величина приведенного дохода от инвестиций, полученного за три года:
а) 34,5 млн руб.;
б) 39,8 млн руб.;
в) 45 млн руб.;
г) 45,8 млн руб.;
д) 50,9 млн руб.
22. Дисконтирующий множитель, показывающий, чему с позиции текущего момента равна 1 денежная единица, планируемая к получению через n периодов при заданной норме доходности r:
а) 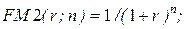
б) 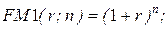
в) 
г) 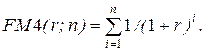
23. Накопленная сумма срочного аннуитета постнумерандо (А - регулярные поступления):
а) 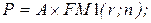
б) 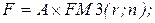
в) 
г) 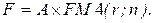
24. Накопленная сумма срочного аннуитета пренумерандо:
а) 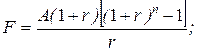
б) 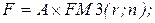
в) 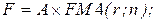
г) 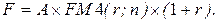
25. Формула  используется для оценки:
используется для оценки:
а) текущей стоимости бессрочного аннуитета
б) будущей стоимости бессрочного аннуитета;
в) текущей стоимости аннуитета постнумерандо;
г) текущей стоимости аннуитета пренумерандо.
26. Дисконтирование срочного аннуитета проводится по формуле:
а) 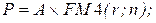
б) 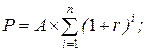
в) 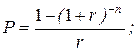
г) 
Дата добавления: 2016-02-02; просмотров: 1877;
