Оценка ценных бумаг и принятие решений по финансовым инвестициям
ЗАДАЧА 8
Оцените текущую стоимость облигации номиналом 10 000 руб., процентной ставкой 10% годовых и сроком погашения через 4 года, если рыночная норма прибыли 8%. Выгодно ли приобретение облигации по курсу 10 500 руб.
Решение.
Сумма ежегодных выплат процентов (С):
С = 10 000×0,1 = 1 000 руб.
Схема денежных поступлений выглядит следующим образом:
| Виды денежных поступлений | Период | |||
| Конец 1 года | Конец 2 года | Конец 3 года | Конец 4 года | |
| Ежегодные проценты (С) | 1 000 | 1 000 | 1 000 | 1 000 |
| Номинальная стоимость (N) | 10 000 |
Для исчисления текущей стоимости облигации (Р) необходимо рассчитать суммарную текущую стоимость данных денежных поступлений:
Р = 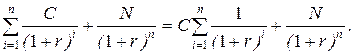
Расчет без использования дисконтирующих множителей:
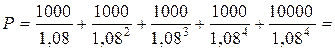
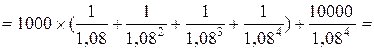 10 662 тыс. руб.
10 662 тыс. руб.
Расчет с применением дисконтирующих множителей:
Первая часть формулы представляет собой аннуитет (денежный поток с равными поступлениями), поэтому для нее используется дисконтирующий множитель FM4(r;n). Вторая часть формулы – однократное поступление, поэтому используем дисконтирующий множитель FM2(r;n).
Р = С × FM4(r;n) + N× FM2(r;n),
Р = 1 000× FM4(8%;4) + 10 000× FM2(8%;4) =
= 1 000×3,312+10 000×0,735 = 10 662 тыс. руб.
Приобретение облигации выгодно при любом курсе, не превышающем ее текущую стоимость (в данном случае последняя характеризует теоретическую ее стоимость при заданной рыночной норме прибыли). Приобретение по курсу ниже текущей стоимости означает, что относительная доходность (по отношению к стоимости приобретения и с учетом временной компоненты) будет выше среднерыночной доходности. Приобретение по курсу, равному текущей стоимости означает равенство доходности по данной ценной бумаге и рыночной. Так как текущая стоимость облигации (10 662 руб.) выше предлагаемого курса (10 500 руб.), облигацию выгодно покупать, чистая текущая (приведенная) стоимость при этом составит 162 руб. (10 662-10 500).
ЗАДАЧА 9
Исчислить текущую стоимость бессрочной облигации, если выплачиваемый по ней годовой доход составляет 1 000 руб., а рыночная доходность – 13%.
Решение.
Используем формулу бессрочного аннуитета:
Р = С : r = 1 000 / 0,13 = 7692,3 руб.
ЗАДАЧА 10
Исчислить текущую стоимость бескупонной облигации (облигации без ежегодных выплат процентов, доход по которой представляет собой дисконт – разницу между ценой приобретения и номиналом) номиналом 10 000 руб., погашаемой через 20 лет, если банковская процентная ставка – 15 %.
Решение.
Р = N / (1+r)n = 10 000 / 1,1520 = 10 000 / 16,367 = 611 руб.
или
Р = N × FM2(r;n) = 10 000× FM2(15%;20) = 10 000 × 0,0611 = 611 руб.
ЗАДАЧА 11
Исчислить текущую стоимость облигации номиналом 10 тыс. руб. с полугодовым начислением процентов, процентной ставкой 12% годовых и сроком погашения через 5 лет, если рыночная норма прибыли: а) 10%; б) 12%; в) 14%.
Решение.
Для расчета используется формула исчисления текущей стоимости облигаций с внутригодовым начислением процентов:
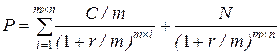 = С/m × FM4 (r/m ; m×n) +
= С/m × FM4 (r/m ; m×n) +
+ N× FM2 (r/m ; m×n),
где С – годовой процентный доход;
m – число внутригодовых начислений процентов;
n – число лет обращения облигации;
r – требуемая норма прибыли (коэффициент дисконтирования);
N – номинал облигации.
По условиям задачи
С = 10 × 12/100 = 1,2 тыс. руб.
а) При рыночной норме прибыли меньшей, чем годовая процентная ставка, облигация будет иметь текущую стоимость выше номинала.
R = 0,1 (10%),
Р = 1,2/2 × FM4 ( 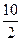 %; 2×5) + 10 × FM2 (
%; 2×5) + 10 × FM2 ( 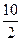 %; 2×5) = 0,6 × FM4 (5%; 10) +
%; 2×5) = 0,6 × FM4 (5%; 10) +
+ 10× FM2 (5%; 10) = 0,6×7,722 + 10×0,614=10,8 тыс. руб.
б) При рыночной норме прибыли равной годовой процентной ставке, облигация будет иметь текущую стоимость равную номиналу.
r=0,12 (12%),
Р = 0,6 × FM4 (6%; 10) + 10× FM2 (6%; 10) = 0,6×7,360 + 10×0,558 =
= 10,0 тыс. руб.
в) При рыночной норме прибыли, превышающей годовую процентную ставку, облигацию выгодно приобретать только по стоимости ниже номинала.
r=0,15 (14%),
Р = 0,6 × FM4 (7%; 10) + 10× FM2 (7%; 10) = 0,6×7,024 + 10×0,508 =
= 9,3 тыс. руб.
ЗАДАЧА 12
Последний выплаченный дивиденд по акции составил 200 руб., темп прироста дивиденда составляет 2% в год. Рассчитать текущую цену акций общества, если требуемая норма прибыли составляет 13%.
Решение.
Текущая стоимость акций с постоянным темпом прироста дивидендов рассчитывается по модели Гордона:
Р = 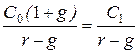 .
.
По условиям задачи дан последний выплаченный дивиденд:
Р = 200 × (1+0,02) / (0,13-0,02) = 1 854,5 руб.
ЗАДАЧА 13
Приобретены акции по курсу 5 тыс. руб., прогнозируемый дивиденд за текущий год составляет 0,2 тыс. руб. Ожидается, что в последующие годы дивиденды будут возрастать с темпом 3%. Рассчитайте приемлемую норму прибыли, использованную инвестором при принятии решения о покупке акций.
Решение.
Поскольку в условиях дан прогнозируемый дивиденд, используется формула:
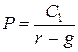 .
.
Откуда:
r = 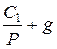 = 0,2 / 5 + 0,03 = 0,07 (7%).
= 0,2 / 5 + 0,03 = 0,07 (7%).
ЗАДАЧА 14
Представлены следующие данные о финансовых активах:
| Финансовый актив А | Финансовый актив Б | ||
| Доходность, % | Вероятность | Доходность, % | Вероятность |
| 0,1 | 0,4 | ||
| 0,3 | 0,3 | ||
| 0,5 | 0,2 | ||
| 0,1 | 0,1 |
Рассчитайте среднеожидаемую доходность, среднеквадратическое (стандартное) отклонение и коэффициент вариации каждого финансового актива. Обоснуйте выбор того или иного проекта.
Решение.
Среднеожидаемая доходность (ko):
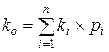 ,
,
где ki – возможная доходность i-го актива;
рi – вероятность проявления.
Среднеквадратическое (стандартное) отклонение (характеризует абсолютный разброс данных вокруг среднего значения) (s):
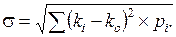
Коэффициент вариации (характеризует относительный разброс данных вокруг среднего значения) (V):
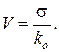
Расчеты произведены в таблицах 1 и 2.
Таблица 1
Расчет среднеожидаемой доходности и показателей вариации
финансового актива А
| Вероятность (рi) | Доходность (ki), % | (ki-ko)2 | (ki-ko)2×рi | Среднее квадратическое отклонение (s) | Коэффициент вариации (V) |
| 4[3×1] | 5 [Öитог гр.4] | 6 [5/2] | |||
| 0,1 | 34,81 | 3,481 | х | х | |
| 0,3 | 8,41 | 2,523 | х | х | |
| 0,5 | 1,21 | 0,605 | х | х | |
| 0,1 | 82,81 | 8,281 | х | х | |
| 1,0 | ko= 15,9 | х | 14,890 | 3,859 | 0,243 |
ko = 10×0,1+13×0,3+17×0,5+25×0,1=15,9%
Таблица 2
Расчет среднеожидаемой доходности и показателей вариации
финансового актива Б
| Вероятность (рi) | Доходность (ki), % | (ki-ko)2 | (ki-ko)2×рi | Среднее квадратическое отклонение (s) | Коэффициент вариации (V) |
| 4[3×1] | 5 [Öитог гр.4] | 6 [5/2] | |||
| 0,4 | 15,21 | 6,084 | Х | х | |
| 0,3 | 0,81 | 0,243 | Х | х | |
| 0,2 | 0,01 | 0,002 | Х | х | |
| 0,1 | 327,61 | 32,761 | х | х | |
| 1,0 | ko= 15,9 | х | 39,090 | 6,252 | 0,393 |
Проекты имеют одинаковую среднеожидаемую доходность (15,9%), поэтому предпочтение следует отдать менее рискованному. Количественно риск в данном случае измеряется среднеквадратическим отклонением и коэффициентом вариации (для случая одинаковой доходности для принятия решения достаточно расчета среднеквадратического отклонения, т.к. знаменатель коэффициента вариации одинаков). Чем выше разброс возможной доходности вокруг среднего значения (выше коэффициент вариации), тем вложения в финансовый актив считаются более рискованными.
В данном случае более рискованными являются вложения в финансовый актив Б: коэффициент вариации 0,393 или 39,3% от среднеожидаемой доходности, в то время как коэффициент вариации актива А значительно ниже: 0,243 или 24,3%. Кроме того, распределение вероятностей показывает, что наиболее вероятная доходность актива А (17% с вероятностью 0,5) выше наиболее вероятной доходности проекта Б (12% с вероятностью 0,4).
ЗАДАЧА 15
Имеются следующие характеристики портфеля ценных бумаг:
| Акции | Общая рыночная стоимость, $ | Бета-коэффициент |
| А | 10 000 | 1,6 |
| Б | 30 000 | 1,2 |
| В | 2 500 | 1,1 |
| Г | 8 000 | 0,9 |
| Д | 7 000 | 0,0 |
Доходность безрисковых ценных бумаг равна 10%, доходность на рынке в среднем – 15%. Рассчитайте доходность и бета портфеля.
Решение.
Модель оценки доходности финансовых активов (Capital Asset Pricing Model, CAPM):
Ko = Kf + b (Km - Kf),
где Ko – ожидаемая доходность акций данной компании;
Kf - доходность безрисковых ценных бумаг (за рубежом таковыми, как правило, считаются государственные ценные бумаги);
Km - средняя доходность на рынке;
b - бета-коэффициент для данной компании.
Бета-коэффициент портфеля (bп) рассчитывается по формуле средневзвешенной:
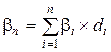 ,
,
где bi – бета-коэффициент i-го актива;
di – доля i-го актива в портфеле.
Ожидаемая доходность портфеля (Коп) может быть исчислена двумя способами:
3) на основании модели CAPM, куда подставляется бета-коэффициент портфеля;
4) по формуле средневзвешенной:
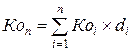 ,
,
где Коi – ожидаемая доходность i-го актива;
di – доля i-го актива в портфеле.
Результаты расчетов будут идентичными.
Таблица 1
Расчет бета-коэффициента и ожидаемой доходности
портфеля ценных бумаг
| Акции | Общая рыночная стоимость, $ | Доля i-го актива в портфеле | Бета-коэффициент (b) | Ожидаемая доходность акций (Ко), % |
| А | 4 [10%+гр.3×(15%-10%] | |||
| А | 10 000 | 0,1739 | 1,60 | 18,0 |
| Б | 30 000 | 0,5217 | 1,20 | 16,0 |
| В | 2 500 | 0,0435 | 1,10 | 15,5 |
| Г | 8 000 | 0,1391 | 0,90 | 14,5 |
| Д | 7 000 | 0,1217 | 0,00 | 10,0 |
| Итого | 57 500 | 1,0000 | 1,08 | 15,4 |
Согласно проведенным расчетам b-коэффициент портфеля выше 1,0 и составляет 1,08. Таким образом, ожидаемая доходность портфеля выше средней рыночной, составляя 15,4%.
Дата добавления: 2016-02-02; просмотров: 1418;
