Базовая концепция инвестиционного анализа и основы
Финансовых вычислений
ЗАДАЧА 1
Определить, какую сумму можно получить через 2 года при вложении 40 тыс. руб. при 10% годовых по схеме сложных процентов (начисленные проценты присоединяются к сумме вклада): 1) начисление процентов один раз в год; 2) начисление процентов ежеквартально.
Решение.
В том случае, если проценты присоединяются к сумме вклада (происходит капитализация процентов), для решения используют формулу сложных процентов:
1) проценты начисляются один раз в год:
F = P 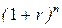 = 40×(1+0,10)2 = 40×1,21 = 48,4 тыс. руб.
= 40×(1+0,10)2 = 40×1,21 = 48,4 тыс. руб.
2) проценты начисляются ежеквартально:
F = 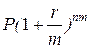 = 40×(1+0,10/4)2×4 = 48,7 тыс. руб.,
= 40×(1+0,10/4)2×4 = 48,7 тыс. руб.,
ЗАДАЧА 2
Определите сумму средств к погашению кредита в размере 2 млн руб., полученного на 30 дней под 20 % годовых.
Решение.
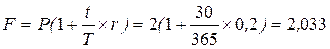 млн руб.
млн руб.
ЗАДАЧА 3
Определить сумму вклада сегодня, чтобы через 2 года иметь накопления 10 тыс. руб. Годовая процентная ставка составляет 10%.
Решение.
По формуле простых процентов (начисление процентов на первоначальную сумму вклада):
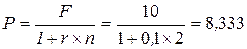 тыс. руб.
тыс. руб.
По формуле сложных процентов (начисление процентов на сумму вклада плюс ранее начисленные проценты):
Р = 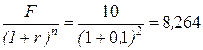 тыс. руб.
тыс. руб.
ЗАДАЧА 4
Достаточно ли величины вклада, равного 10 тыс. руб. под 12% годовых, чтобы через 5 лет оплатить покупку стоимостью 20 тыс. руб.?
Решение.
1 вариант – наращение.
Сумма вклада с процентами к концу срока (F):
F = P 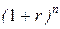 = 10 × (1+0,12)5 = 10 × 1,7623 = 17,623 тыс. руб.
= 10 × (1+0,12)5 = 10 × 1,7623 = 17,623 тыс. руб.
Сумма меньше 20 тыс. руб., т.е. сумма вклада недостаточна.
2 вариант – дисконтирование. Позволяет не только определить, достаточна ли сумма вклада, но и узнать, какую сумму следует вложить сейчас под установленный процент годовых, чтобы через обусловленный срок получить нужную сумму. Текущая стоимость 20 тыс. руб., рассчитываемая по коэффициенту дисконтирования 12% (P):
Р = 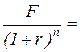 20 / (1+0,12)5 = 20 / 1,7623 = 11,349 тыс. руб.
20 / (1+0,12)5 = 20 / 1,7623 = 11,349 тыс. руб.
P > величины вклада в 10 тыс. руб., т.е. текущая стоимость будущей покупки превышает имеющиеся средства, сумма вклада недостаточна. Необходимо вложить сумму, равную 11,349 тыс. руб.
ЗАДАЧА 5
Рассчитать величину приведенного денежного потока за 4 года: 100, 150, 200, 250 тыс. руб. при ставке дисконтирования (r) 12%.
Решение.
1. Без использования дисконтирующих множителей:
P = 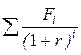 =
= 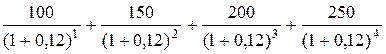 =
=
= 89 + 120 + 142 + 159 = 510 тыс. руб.
2. С применением дисконтирующих множителей:
P = 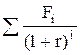 = å Fi×FM2(r;i) = F1×FM2(12%;1) + F2×FM2(12%;2) +
= å Fi×FM2(r;i) = F1×FM2(12%;1) + F2×FM2(12%;2) +
+ F3×FM2(12%;3) + F4×FM2(12%;4) =
= 100×0,8929 + 150×0,7972 + 200×0,7118 + 250×0,6355 = 510 тыс. руб.
3. Используя «Мастер функций» программы Microsoft Exсel. Исходные данные вводятся в строку (столбец) таблицы. В свободной ячейке активируется «Мастер функций». Выбирается функция ЧПС категории «финансовые». В параметре «норма» проставляется значение коэффициента дисконтирования (0,12). В параметре «значение 1» указывается диапазон ячеек, содержащих информацию о денежных потоках (A1:D1).
| А | B | C | D | E | |
| =ЧПС(0,12;A1:D1) | |||||
После нажатия клавиши «Enter» программа рассчитывает значение приведенной (текущей) стоимости.
| А | B | C | D | E | |
| 510,10 | |||||
ЗАДАЧА 6
Заемщик берет в банке кредит в сумме 200 000 руб. сроком на 5 лет под 25% годовых с условием ежегодных выплат (в конце каждого года, начиная с первого) равными суммами (включающими часть основной суммы долга с процентами). Разработать график погашения ссуды, определив ежегодную сумму выплаты, а также выделив выплату основной части долга и процентов.
Решение.
Используем формулу аннуитета:
Р = 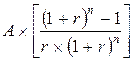 = А × FM4 (r;n).
= А × FM4 (r;n).
Ежегодная сумма выплат (А):
А = Р : 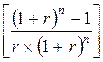 = P : FM4 (r;n).
= P : FM4 (r;n).
По условию задачи FM4 (r;n) = FM4 (25%;5) = 2,68928.
Тогда сумма ежегодных выплат:
А = 200 000 / 2,68928 = 74 369 руб.
Таблица 1
График погашения кредита
| Год | Остаток долга на начало года | Начисление процентов по ставке 25% годовых | Выплаты | ||
| всего | в том числе: | ||||
| процентов | основной суммы долга | ||||
| 6[4-5] | |||||
| 200 000 | 50 000 | 74 369 | 50 000 | 24 369 | |
| 175 631 | 43 908 | 74 369 | 43 908 | 30 461 | |
| 145 170 | 36 292 | 74 369 | 36 292 | 38 077 | |
| 107 093 | 26 773 | 74 369 | 26 773 | 47 596 | |
| 59 497 | 14 874 | 74 372 | 14 874 | 59 497 | |
| Итого | х | 171 848 | 371 848 | 171 848 | 200 000 |
ЗАДАЧА 7
Определить сумму дисконта и вексельного кредита по операции учета векселя в банке за 30 дней до срока погашения. Номинальная стоимость векселя – 100 тыс. руб., ставка дисконта 20 % годовых.
Решение.
Сумма дисконта по операциям досрочного учета векселей:
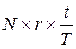 = 100×0,2×30/365 = 1,644 тыс. руб.
= 100×0,2×30/365 = 1,644 тыс. руб.
Сумма вексельного кредита:
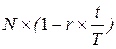 = 100× (1-0,2×30/365) = 100-1,644 = 98,356 тыс. руб.
= 100× (1-0,2×30/365) = 100-1,644 = 98,356 тыс. руб.
Дата добавления: 2016-02-02; просмотров: 2253;
